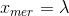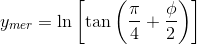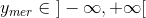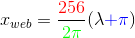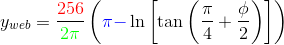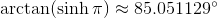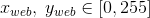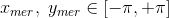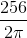Почему разница в значениях масштаба в проекции и плитке?

Question

Используя плагин d3.geo.tile, все примеры имеют различие между масштабом проекции карты и масштабом, переданным функции tile(). Особенно, tile_scale = projection_scale * 2 * Math.PI, Смотрите примеры здесь и здесь.

Что означает это умножение 2 * PI?

Answer 1

Чтобы понять, почему при использовании плагина d3.geo.tile к весам применяется дополнительный коэффициент 2π, важно знать разницу между проекцией, используемой d3.geoMercator() и тот, который используется при построении растровых тайлов.

D3

D3 реализует стандартную проекцию Меркатора по формулам:

Эта проекция использует радиус единичного круга R = 1, центрируясь на меридиане Гринвича. До этого момента не применяется ни масштабирование, ни перевод. Проекция будет выдавать выходные значения из следующих интервалов:

В D3 v4 это реализовано как

export function mercatorRaw(lambda, phi) {
  return [lambda, log(tan((halfPi + phi) / 2))];
}

В D3 v3 использовалось несколько иное обозначение, которое больше напоминает вышеупомянутые формулы, но, конечно, эквивалентно более новой реализации:

function d3_geo_mercator(λ, φ) {
  return [λ, Math.log(Math.tan(π / 4 + φ / 2))];
}

Значения интервалов часто скрыты тем, что d3.geo.mercator() использует значения по умолчанию для перевода и масштабирования. Вы должны явно установить те .translate([0,0]).scale(1) чтобы получить вышеупомянутые интервалы.

плитки

С другой стороны, для плиток используется слегка измененная версия проекции Меркатора, известная как Web Mercator. Соответствующие формулы

В своей основе эта проекция использует те же вычисления, что и стандартная проекция Меркатора. Это можно легко увидеть по слагаемым в черный цвет терминам с правой стороны приведенных выше уравнений, которые в точности совпадают с теми, которые используются проекцией Меркатора. Просто выходные интервалы корректируются, чтобы лучше соответствовать потребностям отображения на экране, применяя некоторое масштабирование и перевод.

Во-первых, проекция отрезана для широты как север, так и юг, превышая

Тем самым проецируя всю карту на квадрат. После этого есть три корректировки (в соответствии с цветом в приведенных выше уравнениях):

1. Переместить начало координат в верхний левый угол (0, 0) - настройка на π синим цветом.
2. Нормализуйте интервалы до [0, 1] - разделите на 2π зеленым цветом
3. Увеличьте масштаб до области 256 × 256 - умножьте на 256 красным цветом.

Это даст выходные значения из интервалов

---

Именно эта разница в масштабах задействованных проекций и является причиной, по которой вам нужно умножить / разделить на 2π. Если вы хотите использовать оба d3.geo.mercator() а также плитки на одной и той же карте, вам нужно изменить шкалы, чтобы они соответствовали друг другу.

Наложение тех же ограничений широты на стандартную проекцию Меркатора, что и в случае проекции Веб-Меркатора, в итоге вы получаете следующие интервалы:

Стандартная проекция Меркатора

Проекты с интервалами

имеющий длину = 2π.

Веб Меркатор Проекция

Проекты с интервалами

имеющий длину = 256.

Это исправлено при установке масштаба проекции как

var projection = d3.geoMercator()
    .scale((1 << 12) / 2 / Math.PI );

Используя простую математику возведения в степень, коэффициент масштабирования можно переписать как

(1 << 4) * (1 << 8) / 2 / Math.PI

и далее

(1 << 4) * 256 / ( 2 * Math.PI )

Первый срок (1 << 4) равно 2 ^4, который является фактическим коэффициентом масштабирования для использования: 16. Это получит плитки с уровнем увеличения 4. Следующий срок

это поправочный коэффициент для корректировки шкал, который включает в себя 2π, о которых был задан ваш вопрос.

Answer 2

Некоторые из d3 прогнозы, в том числе d3.geo.mercator (используется в этих примерах) имеет естественную шкалу с долготой в диапазоне от -π в π:

var s = d3.geo.mercator().translate([0,0]).scale(1);
s([180, 0]); // [3.141592653589793, 0]
s([-180, 0]); // [-3.141592653589793, 0]

Это простой масштаб по умолчанию, потому что, как вы можете видеть в d3.geo.mercator проекция ( формула Википедии), проекция x значение масштабируется линейно с углом долготы. Это имеет смысл, если вы думаете о проекции Веб-Меркатора как о разворачивании и выравнивании идеальной сферы - 1 градус по окружности сферы будет равен 1 единице x расстояние. Таким образом, реализация D3 вообще не масштабирует долготу - она ​​просто возвращает ее как x значение ( см. код). Долгота является входом для этой функции в радианах, поэтому она имеет естественный диапазон от -π в πт.е. 2π угол, описывающий полную окружность круга.

Но главное заключается в том, что масштабные коэффициенты для каждой шкалы являются фактически произвольными и не согласованными между проекциями.

В общем, 2 * Math.PI представляет максимальный диапазон шкалы, а деление на этот коэффициент означает нормализацию этого диапазона до 1 для облегчения математики.