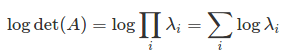Рассчитать журнал определителя в TensorFlow, когда определитель переполнен / недополнен
Моя функция стоимости включает вычисление log(det(A)) (при условии, что det (A) положительна, поэтому лог имеет смысл, но A не является эрмитовой, так что разложение Холецкого здесь неприменимо). Когда det (A) очень большой / маленький, прямой вызов det (A) будет переполнен / переполнен. Чтобы обойти это, можно использовать математический факт, что
log (дет (A)) = Tr(log(A)),
где последние могут быть оценены с использованием разложения LU (которое более эффективно, чем собственное значение /SVD). Этот алгоритм был реализован в numpy как numpy.linalg.slogdet, поэтому проблема заключается в том, как вызвать numpy из TensorFlow.
Вот что я пробовал
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import function
def logdet_np(a):
_, l = np.linalg.slogdet(a)
return l
def logdet1(a):
return tf.py_func(logdet_np, [a], tf.float64)
@function.Defun(tf.float64, func_name='LogDet')
def logdet2(a):
return tf.py_func(logdet_np, [a], tf.float64)
with tf.Session() as sess:
a = tf.constant(np.eye(500)*10.)
#print(sess.run(logdet1(a)))
print(sess.run(logdet2(a)))
Сначала я определяю функцию python для выдачи результата numpy. Затем я определил два logdet функции, использующие tf.py_func, Вторая функция украшена function.Defun который используется для определения функций TensorFlow и их градиентов позже. Когда я проверял их, я обнаружил, что первая функция logdet1 работает и дает правильный результат. Но вторая функция logdet2 возвращает KeyError.
---------------------------------------------------------------------------
KeyError Traceback (most recent call last)
/Library/Frameworks/Python.framework/Versions/3.5/lib/python3.5/site-
packages/tensorflow/python/ops/script_ops.py in __call__(self, token, args)
77 def __call__(self, token, args):
78 """Calls the registered function for `token` with args."""
---> 79 func = self._funcs[token]
80 if func is None:
81 raise ValueError("callback %s is not found" % token)
KeyError: 'pyfunc_0'
Мой вопрос: что не так с Defun декоратор? Почему это противоречит py_func? Как правильно обернуть NumPy функции в TensorFlor?
Оставшаяся часть определения градиента для logdet связано с вопросом матричной детерминанты дифференцирования в тензорном потоке. Согласно решению в этом вопросе, один пытается написать
@function.Defun(tf.float64, tf.float64, func_name='LogDet_Gradient')
def logdet_grad(a, grad):
a_adj_inv = tf.matrix_inverse(a, adjoint=True)
out_shape = tf.concat([tf.shape(a)[:-2], [1, 1]], axis=0)
return tf.reshape(grad, out_shape) * a_adj_inv
@function.Defun(tf.float64, func_name='LogDet', grad_func=logdet_grad)
def logdet(a):
return tf.py_func(logdet_np, [a], tf.float64, stateful=False, name='LogDet')
Приведенный выше код будет работать, если можно решить конфликт между Defun а также py_func, который является ключевым вопросом, который я поднял выше.
3 ответа
С помощью @MaxB здесь я выкладываю код для определения функции logdet для log(abs(det(A))) и его градиент.
logdetвызывает функцию numpy numpy.linalg.slogdet для вычисления лога определителя, используя идею log(det(A))=Tr(log(A)), которая устойчива к переполнению / недостаточному определению детерминанта. Он основан на разложении LU, которое является более эффективным по сравнению с методом на основе собственных значений /SVD.Функция numpy
slogdetвозвращает кортеж, содержащий как знак определителя, так и лог (abs (det (A))). Знак будет игнорироваться, так как он не будет вносить вклад в сигнал градиента при оптимизации.Градиент
logdetвычисляется путем обращения матрицы в соответствии с grad log(det(A)) = inv(A)^T. Он основан на коде TensorFlow на _MatrixDeterminantGrad с небольшими изменениями.
import numpy as np
import tensorflow as tf
# from https://gist.github.com/harpone/3453185b41d8d985356cbe5e57d67342
# Define custom py_func which takes also a grad op as argument:
def py_func(func, inp, Tout, stateful=True, name=None, grad=None):
# Need to generate a unique name to avoid duplicates:
rnd_name = 'PyFuncGrad' + str(np.random.randint(0, 1E+8))
tf.RegisterGradient(rnd_name)(grad) # see _MySquareGrad for grad example
g = tf.get_default_graph()
with g.gradient_override_map({"PyFunc": rnd_name}):
return tf.py_func(func, inp, Tout, stateful=stateful, name=name)
# from https://github.com/tensorflow/tensorflow/blob/master/tensorflow/python/ops/linalg_grad.py
# Gradient for logdet
def logdet_grad(op, grad):
a = op.inputs[0]
a_adj_inv = tf.matrix_inverse(a, adjoint=True)
out_shape = tf.concat([tf.shape(a)[:-2], [1, 1]], axis=0)
return tf.reshape(grad, out_shape) * a_adj_inv
# define logdet by calling numpy.linalg.slogdet
def logdet(a, name = None):
with tf.name_scope(name, 'LogDet', [a]) as name:
res = py_func(lambda a: np.linalg.slogdet(a)[1],
[a],
tf.float64,
name=name,
grad=logdet_grad) # set the gradient
return res
Можно проверить это logdet работает для очень большого / малого определителя, и его градиент также является правильным.
i = tf.constant(np.eye(500))
x = tf.Variable(np.array([10.]))
y = logdet(x*i)
dy = tf.gradients(y, [x])
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print(sess.run([y, dy]))
Результат: [1151.2925464970251, [array([ 50.])]]
Если ваша проблема - переполнение, вы можете бороться с ней с помощью простой математики. 
Так что вам просто нужно получить собственные значения, записать их и суммировать.
Вы можете использовать SVD для разложения A:
A = U S V'
Поскольку определитель продукта является произведением определителей, а определители U а также V' 1 или -1, в то время как определитель S неотрицателен,
abs(det(A)) = det(S)
Следовательно, log (положительного) определителя может быть вычислено как
tf.reduce_sum(tf.log(svd(A, compute_uv=False)))
По состоянию на TF1.1, tf.svd отсутствует градиент (возможно, в будущих версиях он будет), и поэтому я предлагаю принять реализацию из кода kofd: