Что такое простое английское объяснение обозначения "Big O"?
Я бы предпочел как можно меньше формального определения и простую математику.
43 ответа
Быстрое замечание, это почти наверняка путает нотацию Big O (которая является верхней границей) с нотацией Theta (которая является двухсторонней границей). По моему опыту, это на самом деле типично для дискуссий в неакадемических условиях. Извиняюсь за путаницу.
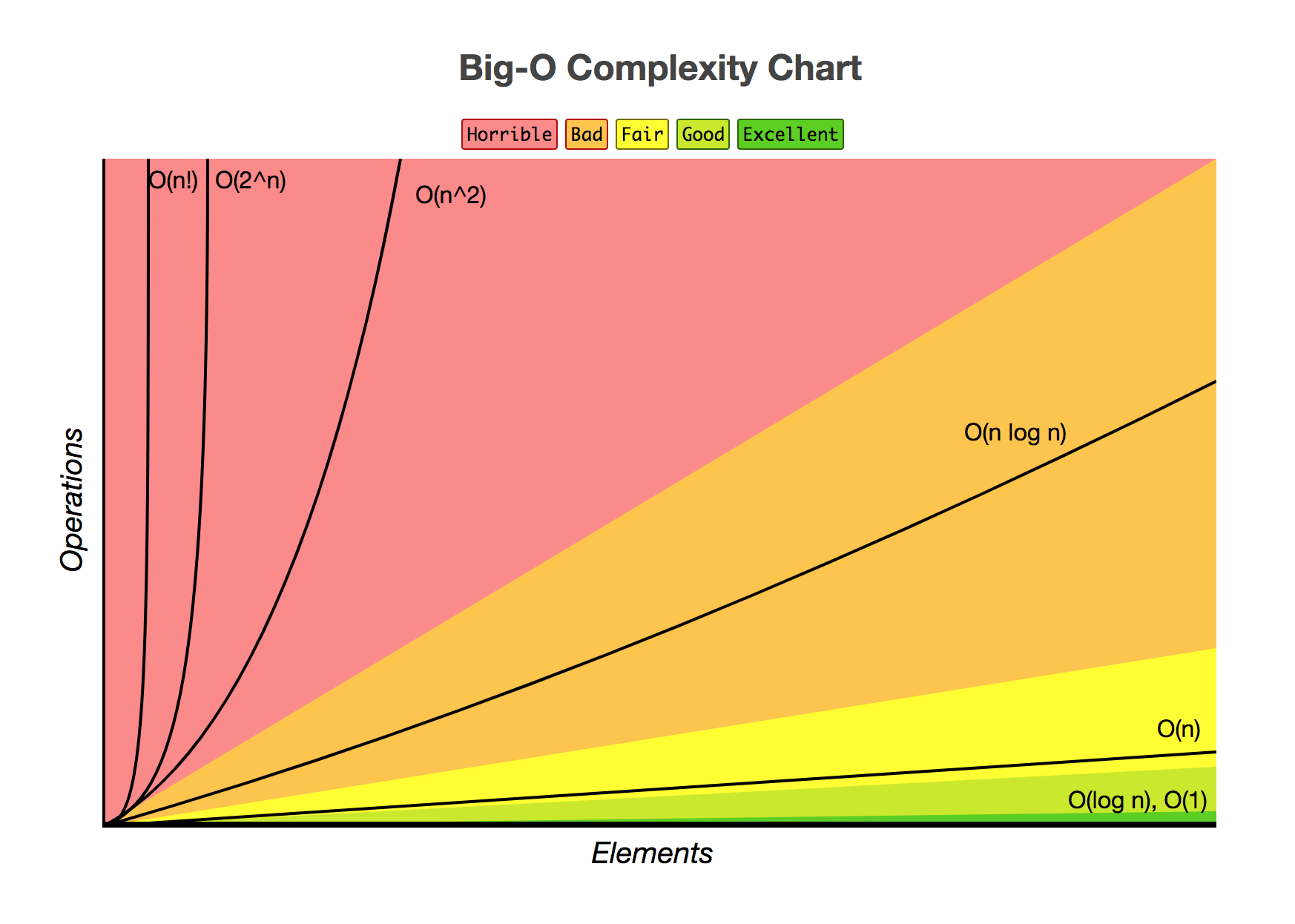
Сложность Big O можно представить с помощью этого графика:
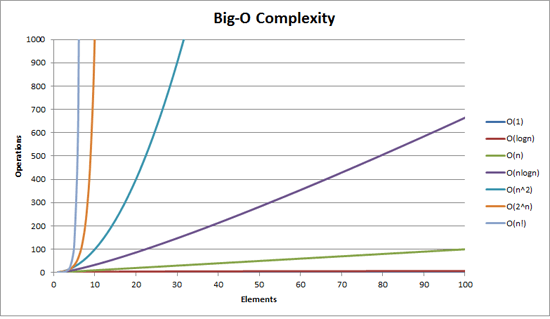
Самое простое определение, которое я могу дать для обозначения Big-O, это:
Система обозначений Big-O является относительным представлением сложности алгоритма.
В этом предложении есть несколько важных и намеренно выбранных слов:
- родственник: вы можете сравнить только яблоки с яблоками. Вы не можете сравнить алгоритм для выполнения арифметического умножения с алгоритмом, который сортирует список целых чисел. Но сравнение двух алгоритмов для выполнения арифметических операций (одно умножение, одно сложение) скажет вам что-то значимое;
- представление: Big-O (в простейшем виде) сводит сравнение между алгоритмами к одной переменной. Эта переменная выбирается на основе наблюдений или предположений. Например, алгоритмы сортировки обычно сравниваются на основе операций сравнения (сравнение двух узлов для определения их относительного порядка). Это предполагает, что сравнение стоит дорого. Но что, если сравнение дешево, а обмен дорог? Это меняет сравнение; а также
- сложность: если мне понадобится одна секунда, чтобы отсортировать 10000 элементов, сколько времени мне понадобится, чтобы отсортировать миллион? Сложность в этом случае является относительной мерой к чему-то другому.
Вернитесь и перечитайте вышеизложенное, когда прочтете все остальное.
Лучший пример Big-O, о котором я могу думать, - это арифметика. Возьмите два числа (123456 и 789012). Основными арифметическими операциями, которые мы изучали в школе, были:
- добавление;
- вычитание;
- умножение; а также
- разделение.
Каждый из них является операцией или проблемой. Метод решения этих проблем называется алгоритмом.
Дополнение самое простое. Вы выравниваете числа вверх (вправо) и добавляете цифры в столбце, записывая последний номер этого сложения в результате. Часть "десятки" этого числа переносится в следующий столбец.
Давайте предположим, что сложение этих чисел является самой дорогой операцией в этом алгоритме. Само собой разумеется, что для сложения этих двух чисел мы должны сложить вместе 6 цифр (и, возможно, 7). Если мы добавим два 100-значных числа вместе, мы должны сделать 100 добавлений. Если мы добавим два числа из 10 000 цифр, мы должны сделать 10 000 дополнений.
Видите образец? Сложность (количество операций) прямо пропорциональна количеству цифр n в большем числе. Мы называем это O(n) или линейной сложностью.
Вычитание аналогично (за исключением того, что вам может понадобиться брать взаймы вместо переноса).
Умножение другое. Вы выстраиваете числа вверх, берете первую цифру в нижнем числе и умножаете ее по очереди на каждую цифру в верхнем числе и так далее до каждой цифры. Таким образом, чтобы умножить наши два 6-значных чисел, мы должны сделать 36 умножений. Возможно, нам понадобится добавить 10 или 11 столбцов, чтобы получить конечный результат.
Если у нас есть два 100-значных числа, нам нужно сделать 10 000 умножений и 200 сложений. Для двух миллионных чисел нам нужно сделать триллион (1012) умножений и два миллиона сложений.
Поскольку алгоритм масштабируется с n-квадратом, это O (n2) или квадратичная сложность. Самое время представить еще одну важную концепцию:
Мы заботимся только о самой значительной части сложности.
Проницательный, возможно, понял, что мы могли бы выразить количество операций как: n2 + 2n. Но, как вы видели из нашего примера с двумя числами в миллион цифр за штуку, второе слагаемое (2n) становится незначительным (составляя 0,0002% от общего числа операций на этом этапе).
Можно заметить, что мы предположили худший вариант развития событий здесь. При умножении 6-значных чисел, если одно из них является 4-значным, а другое - 6-значным, то мы имеем только 24 умножения. Тем не менее мы рассчитываем сценарий наихудшего случая для этого 'n', т.е. когда оба являются 6-значными числами. Следовательно, нотация Big-O относится к наихудшему сценарию алгоритма
Телефонная книга
Следующий лучший пример, который я могу вспомнить, - это телефонная книга, обычно называемая Белыми страницами, или похожая, но она будет варьироваться от страны к стране. Но я говорю о том, кто перечисляет людей по фамилии, а затем инициалы или имя, возможно, адрес, а затем номера телефонов.
Теперь, если бы вы указали компьютеру найти номер телефона "Джона Смита" в телефонной книге, содержащей 1000000 имен, что бы вы сделали? Игнорируя тот факт, что вы можете догадаться, как далеко в S началось (предположим, вы не можете), что бы вы сделали?
Типичная реализация может состоять в том, чтобы открыть до середины, взять 500 000-й и сравнить его со "Смитом". Если это "Смит, Джон", нам просто повезло. Гораздо более вероятно, что "Джон Смит" будет до или после этого имени. Если это после того, как мы разделим вторую половину телефонной книги пополам и повторите. Если это раньше, то мы разделяем первую половину телефонной книги пополам и повторяем. И так далее.
Это называется бинарным поиском и используется каждый день в программировании, понимаете ли вы это или нет.
Поэтому, если вы хотите найти имя в телефонной книге из миллиона имен, вы можете найти любое имя, выполнив это не более 20 раз. Сравнивая алгоритмы поиска, мы решаем, что это сравнение - наше "n".
- Для телефонной книги с 3 именами требуется 2 сравнения (самое большее).
- Для 7 требуется максимум 3.
- Для 15 требуется 4.
- ...
- На 1000000 это займет 20.
Это потрясающе хорошо, не правда ли?
В терминах Big-O это O(log n) или логарифмическая сложность. Теперь рассматриваемый логарифм может быть ln (база e), log10, log2 или какая-то другая база. Неважно, что это все еще O(log n), точно так же, как O (2n2) и O (100n2) все еще оба O (n2).
На этом этапе стоит объяснить, что Big O можно использовать для определения трех случаев с помощью алгоритма:
- Лучший случай: в поиске по телефонной книге лучший случай - это то, что мы находим имя в одном сравнении. Это O(1) или постоянная сложность;
- Ожидаемый случай: как обсуждалось выше, это O(log n); а также
- В худшем случае: это тоже O(log n).
Обычно мы не заботимся о лучшем случае. Нас интересует ожидаемый и наихудший случай. Иногда один или другой из них будет более важным.
Вернуться к телефонной книге.
Что делать, если у вас есть номер телефона и вы хотите найти имя? У полиции есть обратная телефонная книга, но такие просмотры запрещены для широкой публики. Или они? Технически вы можете отменить поиск номера в обычной телефонной книге. Как?
Вы начинаете с первого имени и сравниваете число. Если это совпадение, отлично, если нет, переходите к следующему. Вы должны сделать это таким образом, потому что телефонная книга неупорядочена (по номеру телефона в любом случае).
Итак, чтобы найти имя по номеру телефона (обратный поиск):
- Лучший случай: O(1);
- Ожидаемый случай: O(n) (для 500 000); а также
- В худшем случае: O(n) (для 1 000 000).
Коммивояжер
Это довольно известная проблема в информатике и заслуживает упоминания. В этой задаче у вас N городов. Каждый из этих городов связан с одним или несколькими другими городами дорогой определенного расстояния. Задача коммивояжера - найти кратчайший тур, который посещает каждый город.
Звучит просто? Подумай еще раз.
Если у вас есть 3 города A, B и C с дорогами между всеми парами, то вы можете пойти:
- A → B → C
- A → C → B
- B → C → A
- B → A → C
- C → A → B
- C → B → A
Ну, на самом деле это меньше, потому что некоторые из них эквивалентны (A → B → C и C → B → A эквивалентны, например, потому что они используют одни и те же дороги, только наоборот).
На самом деле есть 3 возможности.
- Отнесите это в 4 города, и у вас будет (iirc) 12 возможностей.
- С 5 это 60.
- 6 становится 360.
Это функция математической операции, называемой факториалом. В принципе:
- 5! = 5 × 4 × 3 × 2 × 1 = 120
- 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
- 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
- ...
- 25! = 25 × 24 × … × 2 × 1 = 15,511,210,043,330,985,984,000,000
- ...
- 50! = 50 × 49 × … × 2 × 1 = 3,04140932 × 1064
Таким образом, основной проблемой задачи коммивояжера является O(n!) Или факторная или комбинаторная сложность.
К тому времени, как вы доберетесь до 200 городов, во вселенной не останется достаточно времени, чтобы решить проблему с традиционными компьютерами.
Что-то думать о.
Полиномиальное время
Еще один момент, о котором я хотел бы кратко упомянуть, заключается в том, что любой алгоритм со сложностью O (na) называется полиномиальной сложностью или разрешим в полиномиальном времени.
O(n), O (n2) и т. Д. - все полиномиальное время. Некоторые проблемы не могут быть решены за полиномиальное время. Из-за этого в мире используются определенные вещи. Криптография с открытым ключом является ярким примером. В вычислительном отношении трудно найти два простых фактора очень большого числа. Если бы это было не так, мы бы не смогли использовать системы открытых ключей, которые мы используем.
Во всяком случае, это все для моего (надеюсь простого английского) объяснения Big O (исправлено).
Это показывает, как алгоритм масштабируется.
O (n2): известен как квадратичная сложность
- 1 предмет: 1 секунда
- 10 предметов: 100 секунд
- 100 предметов: 10000 секунд
Обратите внимание, что количество предметов увеличивается в 10 раз, но время увеличивается в 102 раза. В основном, n=10, и поэтому O (n2) дает нам коэффициент масштабирования n2, который равен 102.
O(n): известен как линейная сложность
- 1 предмет: 1 секунда
- 10 предметов: 10 секунд
- 100 предметов: 100 секунд
На этот раз количество предметов увеличивается в 10 раз, как и время. n=10 и поэтому коэффициент масштабирования O(n) равен 10.
O(1): известный как постоянная сложность
- 1 предмет: 1 секунда
- 10 предметов: 1 секунда
- 100 предметов: 1 секунда
Количество элементов все еще увеличивается в 10 раз, но коэффициент масштабирования O(1) всегда равен 1.
O (log n): известный как логарифмическая сложность
- 1 предмет: 1 секунда
- 10 предметов: 2 секунды
- 100 предметов: 3 секунды
- 1000 предметов: 4 секунды
- 10000 предметов: 5 секунд
Количество вычислений увеличивается только путем записи входного значения. Так что в этом случае, предполагая, что каждое вычисление занимает 1 секунду, журнал ввода n требуется время, следовательно log n,
Это суть этого. Они уменьшают математику, так что это может быть не ровно n2 или что они там говорят, но это будет доминирующим фактором в масштабировании.
Нотация Big-O (также называемая нотацией "асимптотического роста") - это то, на что "похожи" функции, когда вы игнорируете постоянные множители и прочее около начала координат. Мы используем это, чтобы говорить о том, как вещи масштабируются.
основы
для "достаточно" больших входов...
f(x) ∈ O(upperbound)средстваf"растет не быстрее чем"upperboundf(x) ∈ Ɵ(justlikethis)имею в видуf"растет так же, как"justlikethisf(x) ∈ Ω(lowerbound)средстваf"растет не медленнее чем"lowerbound
нотация big-O не заботится о постоянных факторах: функция 9x² Говорят, "расти точно так же, как" 10x², Асимптотическая система обозначений big-O также не заботится о неасимптотических вещах ("вещи рядом с источником" или "что происходит, когда размер задачи мал"): функция 10x² Говорят, "расти точно так же, как" 10x² - x + 2,
Почему вы хотите игнорировать меньшие части уравнения? Потому что они сильно затмеваются большими частями уравнения, если учесть все большие и большие масштабы; их вклад становится карликовым и неактуальным. (Смотрите пример раздела.)
Иными словами, все зависит от соотношения, когда вы идете в бесконечность. Если вы разделите фактическое время, которое занимает O(...) , вы получите постоянный фактор в пределе больших входов. Интуитивно это имеет смысл: функции "масштабируются как" друг друга, если вы можете умножить одну, чтобы получить другую. То есть когда мы говорим...
actualAlgorithmTime(N) ∈ O(bound(N))
e.g. "time to mergesort N elements
is O(N log(N))"
... это означает, что для "достаточно больших" размеров задач N (если мы игнорируем вещи около начала координат), существует некоторая постоянная (например, 2.5, полностью составленная) такая, что:
actualAlgorithmTime(N) e.g. "mergesort_duration(N) "
────────────────────── < constant ───────────────────── < 2.5
bound(N) N log(N)
Есть много вариантов констант; часто "лучший" выбор известен как "постоянный фактор" алгоритма... но мы часто игнорируем его, как игнорируем не самые большие термины (см. раздел "Постоянные факторы", почему они обычно не имеют значения). Вы также можете думать о приведенном выше уравнении как о границе, говоря: " В худшем случае время, которое оно занимает, никогда не будет хуже, чем примерно N*log(N) с коэффициентом 2,5 (постоянный фактор, нас не волнует) ".
В общем, O(...) является наиболее полезным, потому что мы часто заботимся о худшем поведении. Если f(x) представляет что-то "плохое", например, использование процессора или памяти f(x) ∈ O(upperbound) " средства " upperbound наихудший сценарий использования процессора / памяти ".
Приложения
Как чисто математическая конструкция, нотация big-O не ограничивается разговорами о времени обработки и памяти. Вы можете использовать это, чтобы обсудить асимптотику всего, где масштабирование имеет смысл, например:
- количество возможных рукопожатий среди
Nлюди на вечеринке (Ɵ(N²)конкретноN(N-1)/2, но важно то, что он "масштабируется как"N²) - вероятностное ожидаемое количество людей, которые видели какой-то вирусный маркетинг как функцию времени
- как задержка веб-сайта масштабируется с количеством процессорных блоков в CPU, GPU или компьютерном кластере
- как тепловая мощность на процессоре умирает в зависимости от количества транзисторов, напряжения и т. д.
- сколько времени нужно запустить алгоритму в зависимости от размера ввода
- сколько места нужно запустить алгоритму в зависимости от размера ввода
пример
Для приведенного выше примера рукопожатия все в комнате пожимают друг другу руки. В этом примере #handshakes ∈ Ɵ(N²), Зачем?
Сделайте небольшое резервное копирование: количество рукопожатий ровно n-выбирать-2 или N*(N-1)/2 (каждый из N человек пожимает руку N-1 другим людям, но это двойное количество рукопожатий, так что разделите на 2):
Тем не менее, для очень большого числа людей, линейный термин N Вычеркивается и эффективно добавляет 0 к отношению (на диаграмме: доля пустых ящиков на диагонали по отношению к общему количеству ящиков уменьшается по мере увеличения числа участников). Следовательно, поведение масштабирования order N² или количество рукопожатий "растет как N²".
#handshakes(N)
────────────── ≈ 1/2
N²
Это как если бы пустых полей на диагонали диаграммы (N*(N-1)/2 галочки) даже не было (асимптотически N 2 галочки).
(временное отступление от "простого английского":) Если вы хотите доказать это себе, вы можете выполнить некоторую простую алгебру отношения, чтобы разделить его на несколько терминов (lim означает "рассматривается в пределе", просто игнорируйте его, если вы его не видели, это просто обозначение "и N действительно очень большой"):
N²/2 - N/2 (N²)/2 N/2 1/2
lim ────────── = lim ( ────── - ─── ) = lim ─── = 1/2
N→∞ N² N→∞ N² N² N→∞ 1
┕━━━┙
this is 0 in the limit of N→∞:
graph it, or plug in a really large number for N
tl; dr: количество рукопожатий "выглядит как" x² настолько для больших значений, что если бы мы записали соотношение #handshakes/x², тот факт, что нам не нужны именно x² рукопожатия, даже не обнаружился бы в десятичном виде для сколь угодно большого времени.
например, для x=1 миллион, отношение # рукопожатия /x²: 0,499999...
Интуиция здания
Это позволяет нам делать заявления как...
"Для достаточно большого входного размера =N, независимо от того, каков постоянный коэффициент, если я удваиваю входной размер...
- ... Я удваиваю время, затрачиваемое алгоритмом O(N) ("линейное время"). "
N → (2N) = 2 (N)
- ... Я удваиваю квадратичное (четырехкратное) время, затрачиваемое алгоритмом O(N²) ("квадратичное время"). " (Например, задача 100x как большая занимает 100²=10000x как долго... возможно, неустойчиво)
N² → (2N) ² = 4 (N²)
- ... Я удваиваю кубы (в восьмерике) времени, которое занимает алгоритм O(N³) ("кубическое время"). " (Например, задача 100x большого размера занимает 100³=1000000x длинного... очень неустойчиво)
cN³ → c (2N) ³ = 8 (cN³)
- ... я добавляю фиксированное количество ко времени, которое занимает алгоритм O(log(N)) ("логарифмическое время"). " (Дешево!)
c log (N) → c log (2N) = (c log (2)) + (c log (N)) = (фиксированная сумма) + (c log (N))
- ... Я не изменяю время, которое занимает алгоритм O(1) ("постоянное время"). " (Самый дешевый!)
с * 1 → с * 1
- ... Я "(в основном) удваиваю" время, которое занимает алгоритм O(N log(N)). " (Довольно часто)
это меньше, чем O (N 1.000001), который вы могли бы назвать в основном линейным
- ... Я смехотворно увеличиваю время, затрачиваемое алгоритмом O (2 N) ("экспоненциальное время"). " (Вы удвоите (или утроите и т. Д.) Время, просто увеличив проблему на единицу)
2 N → 2 2N = (4 N)............ другими словами...... 2 N → 2 N + 1 = 2 N 2 1 = 2 2 N
[для математически склонных, вы можете навести курсор мыши на спойлеры для незначительных признаков)
(с благодарностью за /questions/39021821/chto-takoe-prostoe-anglijskoe-obyasnenie-oboznacheniya-big-o/39021854#39021854)
(технически постоянный фактор может иметь значение в некоторых более эзотерических примерах, но я сформулировал выше (например, в журнале (N)), что это не так)
Это те залы роста, которые программисты и прикладные компьютерные ученые используют как ориентиры. Они видят это все время. (Таким образом, хотя вы могли бы технически подумать: "Удвоение ввода делает алгоритм O(√N) в 1,414 раз медленнее", лучше думать об этом как "это хуже, чем логарифмический, но лучше, чем линейный".)
Постоянные факторы
Обычно нас не волнуют конкретные константные факторы, потому что они не влияют на то, как растет функция. Например, два алгоритма могут оба O(N) время для завершения, но один может быть в два раза медленнее, чем другой. Нас, как правило, не волнует слишком много, если фактор не очень велик, так как оптимизация - сложная задача ( когда оптимизация преждевременна?); Кроме того, простое действие выбора алгоритма с лучшим значением big-O часто повышает производительность на порядки.
Некоторые асимптотически превосходные алгоритмы (например, несопоставление O(N log(log(N))) сортировка) может иметь такой большой постоянный коэффициент (например, 100000*N log(log(N))), или относительно большие, как O(N log(log(N))) со скрытым + 100*N, что их редко стоит использовать даже на "больших данных".
Почему O (N) иногда лучшее, что вы можете сделать, то есть, почему нам нужны структуры данных
O(N) алгоритмы в некотором смысле являются "лучшими" алгоритмами, если вам нужно прочитать все ваши данные. Сам акт чтения группы данных является O(N) операция. Загрузка его в память обычно O(N) (или быстрее, если у вас есть аппаратная поддержка, или совсем нет времени, если вы уже прочитали данные). Однако, если вы коснетесь или даже посмотрите на каждый фрагмент данных (или даже на любой другой фрагмент данных), ваш алгоритм займет O(N) время, чтобы выполнить этот взгляд. Nomatter, как долго ваш фактический алгоритм займет, это будет по крайней мере O(N) потому что он потратил время на просмотр всех данных.
То же самое можно сказать и о самом акте письма. Все алгоритмы, которые распечатывают N вещей, будут занимать N времени, потому что вывод будет по крайней мере таким длинным (например, распечатка всех перестановок (способов перестановки) набора из N игральных карт является факториальной: O(N!)).
Это мотивирует использование структур данных: структура данных требует чтения данных только один раз (обычно O(N) время), плюс некоторое произвольное количество предварительной обработки (например, O(N) или же O(N log(N)) или же O(N²)) которые мы стараемся держать маленькими. После этого изменение структуры данных (вставки / удаления / и т. Д.) И выполнение запросов к данным занимают очень мало времени, например O(1) или же O(log(N)), Затем вы приступаете к выполнению большого количества запросов! В целом, чем больше работы вы готовы выполнить раньше времени, тем меньше работы вам придется выполнять позже.
Например, скажем, у вас были координаты широты и долготы миллионов отрезков дорог, и вы хотели найти все перекрестки улиц.
- Наивный метод: если у вас есть координаты пересечения улиц и вы хотите исследовать близлежащие улицы, вам придется каждый раз проходить миллионы отрезков и проверять каждый из них на смежность.
- Если бы вам нужно было сделать это только один раз, не было бы проблемой сделать наивный метод
O(N)работать только один раз, но если вы хотите сделать это много раз (в этом случае,Nраз, один раз для каждого сегмента), мы должны сделатьO(N²)работа или 1000000²=1000000000000 операций. Не хорошо (современный компьютер может выполнять около миллиарда операций в секунду). - Если мы используем простую структуру, называемую хеш-таблицей (таблица поиска с мгновенной скоростью, также известная как хэш-карта или словарь), мы платим небольшую плату, предварительно обрабатывая все в
O(N)время. После этого в среднем требуется только постоянное время, чтобы найти что-то по его ключу (в этом случае наш ключ - это координаты широты и долготы, округленные в сетку; мы ищем соседние сеточные пространства, которых всего 9, что является константа). - Наша задача пошла от неосуществимого
O(N²)к управляемомуO(N)и все, что нам нужно было сделать, это заплатить небольшую плату за создание хеш-таблицы. - аналогия: аналогия в данном конкретном случае представляет собой головоломку: мы создали структуру данных, которая использует некоторое свойство данных. Если наши сегменты дороги похожи на кусочки головоломки, мы группируем их по цвету и рисунку. Затем мы используем это, чтобы избежать дополнительной работы позже (сравнивая кусочки головоломки одинакового цвета друг с другом, а не со всеми остальными кусочками головоломки).
Мораль этой истории: структура данных позволяет нам ускорить работу. Даже более продвинутые структуры данных позволяют невероятно умным образом комбинировать, задерживать или даже игнорировать операции. Разные проблемы будут иметь разные аналогии, но все они будут включать в себя организацию данных таким образом, чтобы использовать некоторую структуру, которая нам небезразлична, или которую мы искусственно навязали ей для учета. Мы работаем раньше времени (в основном, планируя и организовывая), и теперь повторять задачи намного проще!
Практический пример: визуализация порядка роста при кодировании
Асимптотическая запись по своей сути совершенно отделена от программирования. Асимптотическая нотация - это математическая основа для размышлений о масштабировании вещей, которая может использоваться во многих различных областях. Тем не менее... это то, как вы применяете асимптотические обозначения для кодирования.
Основы: всякий раз, когда мы взаимодействуем с каждым элементом в коллекции размера A (таким как массив, набор, все ключи карты и т. Д.), Или выполняем итерации цикла, то есть множитель множителя размера A Почему я говорю "мультипликативный фактор"?- потому что циклы и функции (почти по определению) имеют мультипликативное время выполнения: количество итераций, время работы, выполненной в цикле (или для функций: количество раз, которое вы вызываете функция, время работы сделано в функции). (Это справедливо, если мы не делаем ничего сложного, например, пропускаем циклы или рано выходим из цикла, или изменяем поток управления в функции на основе аргументов, что очень часто встречается.) Вот несколько примеров методов визуализации с сопровождающим псевдокодом.
(здесь x s представляют единицы работы в постоянном времени, инструкции процессора, коды операций интерпретатора и т. д.)
for(i=0; i<A; i++) // A * ...
some O(1) operation // 1
--> A*1 --> O(A) time
visualization:
|<------ A ------->|
1 2 3 4 5 x x ... x
other languages, multiplying orders of growth:
javascript, O(A) time and space
someListOfSizeA.map((x,i) => [x,i])
python, O(rows*cols) time and space
[[r*c for c in range(cols)] for r in range(rows)]
Пример 2:
for every x in listOfSizeA: // A * (...
some O(1) operation // 1
some O(B) operation // B
for every y in listOfSizeC: // C * (...
some O(1) operation // 1))
--> O(A*(1 + B + C))
O(A*(B+C)) (1 is dwarfed)
visualization:
|<------ A ------->|
1 x x x x x x ... x
2 x x x x x x ... x ^
3 x x x x x x ... x |
4 x x x x x x ... x |
5 x x x x x x ... x B <-- A*B
x x x x x x x ... x |
................... |
x x x x x x x ... x v
x x x x x x x ... x ^
x x x x x x x ... x |
x x x x x x x ... x |
x x x x x x x ... x C <-- A*C
x x x x x x x ... x |
................... |
x x x x x x x ... x v
Пример 3:
function nSquaredFunction(n) {
total = 0
for i in 1..n: // N *
for j in 1..n: // N *
total += i*k // 1
return total
}
// O(n^2)
function nCubedFunction(a) {
for i in 1..n: // A *
print(nSquaredFunction(a)) // A^2
}
// O(a^3)
Если мы сделаем что-то немного сложное, вы все равно сможете визуально представить, что происходит:
for x in range(A):
for y in range(1..x):
simpleOperation(x*y)
x x x x x x x x x x |
x x x x x x x x x |
x x x x x x x x |
x x x x x x x |
x x x x x x |
x x x x x |
x x x x |
x x x |
x x |
x___________________|
Здесь важен наименьший узнаваемый контур, который вы можете нарисовать; треугольник - это двумерная форма (0,5 A^2), точно так же, как квадрат - это двумерная форма (A^2); постоянный множитель два здесь остается в асимптотическом соотношении между ними, однако мы игнорируем его, как и все факторы... (У этой техники есть некоторые прискорбные нюансы, которые я здесь не рассматриваю; она может ввести вас в заблуждение.)
Конечно, это не означает, что циклы и функции плохие; напротив, они являются строительными блоками современных языков программирования, и мы их любим. Однако мы видим, что способ, которым мы плетем циклы, а также функции и условия вместе с нашими данными (поток управления и т. Д.), Имитирует использование нашей программы во времени и пространстве! Если использование времени и пространства становится проблемой, то тогда мы прибегаем к хитрости и находим простой алгоритм или структуру данных, которые мы не рассматривали, чтобы как-то уменьшить порядок роста. Тем не менее, эти методы визуализации (хотя они не всегда работают) могут дать вам наивное предположение в худшем случае.
Вот еще одна вещь, которую мы можем узнать визуально:
<----------------------------- N ----------------------------->
x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
x x x x x x x x x x x x x x x x
x x x x x x x x
x x x x
x x
x
Мы можем просто изменить это и увидеть, что это O(N):
<----------------------------- N ----------------------------->
x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
x x x x x x x x x x x x x x x x|x x x x x x x x|x x x x|x x|x
Или, может быть, вы делаете log (N) проходов данных, для O(N*log(N)) общего времени:
<----------------------------- N ----------------------------->
^ x x x x x x x x x x x x x x x x|x x x x x x x x x x x x x x x x
| x x x x x x x x|x x x x x x x x|x x x x x x x x|x x x x x x x x
lgN x x x x|x x x x|x x x x|x x x x|x x x x|x x x x|x x x x|x x x x
| x x|x x|x x|x x|x x|x x|x x|x x|x x|x x|x x|x x|x x|x x|x x|x x
v x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x|x
Безотносительно, но стоит упомянуть еще раз: если мы выполняем хеш (например, поиск по словарю / хеш-таблице), это фактор O(1). Это довольно быстро.
[myDictionary.has(x) for x in listOfSizeA]
\----- O(1) ------/
--> A*1 --> O(A)
Если мы делаем что-то очень сложное, например, с помощью рекурсивной функции или алгоритма "разделяй и властвуй", вы можете использовать основную теорему (обычно работает) или, в смешных случаях, теорему Акра-Бацци (почти всегда работает), вы ищите время выполнения вашего алгоритма в Википедии.
Но программисты так не думают, потому что в конечном итоге интуиция алгоритма становится второй натурой. Вы начнете кодировать что-то неэффективное и сразу же подумаете: "Я делаю что-то крайне неэффективное? ". Если ответ "да", и вы предвидите, что это действительно имеет значение, тогда вы можете сделать шаг назад и подумать о различных хитростях, чтобы заставить вещи работать быстрее (ответ почти всегда "использовать хеш-таблицу", редко "использовать дерево", и очень редко что-то более сложное).
Амортизированная и средняя сложность
Существует также понятие "амортизированный" и / или "средний случай" (обратите внимание, что они разные).
Средний регистр: это не более чем использование нотации big-O для ожидаемого значения функции, а не самой функции. В обычном случае, когда вы полагаете, что все входные данные одинаково вероятны, средний случай - это просто среднее время выполнения. Например, с быстрой сортировкой, хотя наихудший случай O(N^2) для некоторых действительно плохих входов средний случай является обычным O(N log(N)) (действительно плохие входные данные очень малы, поэтому их мало, чтобы мы не замечали их в среднем случае).
Амортизированный наихудший случай. Некоторые структуры данных могут иметь сложность в наихудшем случае, которая является большой, но гарантирует, что при выполнении многих из этих операций средний объем выполняемой вами работы будет лучше, чем в худшем случае. Например, у вас может быть структура данных, которая обычно принимает постоянную O(1) время. Тем не менее, иногда это будет "сбой" и принять O(N) время для одной случайной операции, потому что, может быть, ей нужно сделать какую-то бухгалтерию или сборщик мусора или что-то в этом роде... но он обещает вам, что, если он сделает сбой, он больше не будет сбой для еще N операций. Наихудшая цена все еще O(N) за операцию, но амортизированная стоимость за много прогонов O(N)/N знак равно O(1) за операцию. Поскольку большие операции достаточно редки, можно считать, что огромное количество случайных работ сливалось с остальной работой как постоянный фактор. Мы говорим, что работа "амортизируется" по достаточно большому количеству вызовов, что она исчезает асимптотически.
Аналогия для амортизированного анализа:
Вы водите машину. Иногда вам нужно потратить 10 минут на заправку, а затем потратить 1 минуту, заправляя бак бензином. Если бы вы делали это каждый раз, когда ездили на машине куда-либо (потратить 10 минут на машине до заправки, потратить несколько секунд, чтобы заполнить долю галлона), это было бы очень неэффективно. Но если вы заправляете бак раз в несколько дней, 11 минут, потраченные на заправку, "амортизируются" за достаточно большое количество поездок, так что вы можете игнорировать его и делать вид, что все ваши поездки были, возможно, на 5% длиннее.
Сравнение среднего и амортизированного наихудшего случая:
- Средний случай: мы делаем некоторые предположения о наших входных данных; т.е. если наши входы имеют разные вероятности, то наши выходы / время выполнения будут иметь разные вероятности (которые мы берем в среднем). Обычно мы предполагаем, что все наши входные данные одинаково вероятны (равномерная вероятность), но если реальные входные данные не соответствуют нашим предположениям о "среднем входном сигнале", расчеты среднего выходного значения / времени выполнения могут быть бессмысленными. Однако если вы ожидаете равномерно случайных входных данных, об этом полезно подумать!
- Амортизированный наихудший случай: если вы используете амортизированную структуру данных наихудшего случая, производительность гарантированно будет находиться в пределах амортизированного наихудшего случая... в конце концов (даже если входные данные выбираются злым демоном, который знает все и пытается пошутил) Обычно мы используем это для анализа алгоритмов, которые могут быть очень "нестабильными" по производительности с неожиданными большими сбоями, но со временем работают так же, как и другие алгоритмы. (Однако, если ваша структура данных не имеет верхних пределов для большой выдающейся работы, на которую она готова откладывать, злой злоумышленник, возможно, заставит вас наверстать упущенное на максимальном объеме откладываемой работы одновременно.
Хотя, если вы разумно беспокоитесь о злоумышленнике, есть много других алгоритмических векторов атаки, о которых следует беспокоиться, кроме амортизации и среднего случая.)
И средний случай, и амортизация являются невероятно полезными инструментами для размышлений и проектирования с учетом масштабирования.
(См. Разница между средним случаем и амортизированным анализом, если интересует эта подтема.)
Многомерный биг-о
В большинстве случаев люди не понимают, что на работе более одной переменной. Например, в алгоритме поиска строки ваш алгоритм может занять время O([length of text] + [length of query]) то есть он является линейным по двум переменным O(N+M), Другие более наивные алгоритмы могут быть O([length of text]*[length of query]) или же O(N*M), Игнорирование нескольких переменных является одним из наиболее распространенных недостатков, которые я вижу в анализе алгоритмов, и может помешать вам при разработке алгоритма.
Вся история
Имейте в виду, что big-O - это не вся история. Вы можете существенно ускорить некоторые алгоритмы, используя кеширование, делая их не обращающими внимания на кеш, избегая узких мест, работая с оперативной памятью вместо диска, используя распараллеливание или опережая работу - эти методы часто не зависят от порядка роста нотация big-O, хотя вы часто будете видеть количество ядер в нотации big-O параллельных алгоритмов.
Также имейте в виду, что из-за скрытых ограничений вашей программы вы можете не заботиться об асимптотическом поведении. Вы можете работать с ограниченным количеством значений, например:
- Если вы сортируете что-то вроде 5 элементов, вы не хотите использовать быстрый
O(N log(N))быстрая сортировка; Вы хотите использовать сортировку вставкой, которая хорошо работает на небольших входах. Эти ситуации часто встречаются в алгоритмах "разделяй и властвуй", где вы разбиваете задачу на все более мелкие подзадачи, такие как рекурсивная сортировка, быстрые преобразования Фурье или умножение матриц. - Если некоторые значения эффективно ограничены из-за какого-то скрытого факта (например, среднее человеческое имя мягко ограничено, возможно, 40 буквами, а человеческий возраст мягко ограничен около 150). Вы также можете наложить ограничения на ваш ввод, чтобы эффективно сделать условия постоянными.
На практике, даже среди алгоритмов, которые имеют одинаковую или сходную асимптотическую производительность, их относительные достоинства могут фактически зависеть от других факторов, таких как: другие факторы производительности (быстрая сортировка и объединенная сортировка являются O(N log(N)), но быстрая сортировка использует преимущества кэшей процессора); соображения неэффективности, такие как простота реализации; доступна ли библиотека, и насколько авторитетна и поддерживается библиотека.
Программы также будут работать медленнее на компьютере с частотой 500 МГц и 2 ГГц. На самом деле мы не рассматриваем это как часть границ ресурса, потому что мы думаем о масштабировании в терминах машинных ресурсов (например, за тактовый цикл), а не за реальную секунду. Однако есть подобные вещи, которые могут "тайно" влиять на производительность, например, работаете ли вы под эмуляцией или оптимизировал код компилятор или нет. Это может заставить некоторые базовые операции занимать больше времени (даже относительно друг друга) или даже асимптотически ускорять или замедлять некоторые операции (даже относительно друг друга). Эффект может быть небольшим или большим между различными реализациями и / или средой. Вы переключаете языки или машины, чтобы выполнить эту небольшую дополнительную работу? Это зависит от сотен других причин (необходимость, навыки, коллеги, производительность программиста, денежная ценность вашего времени, знакомство, обходные пути, почему бы не сборка или графический процессор и т. Д.), Которые могут быть важнее производительности.
Вышеупомянутые проблемы, такие как язык программирования, почти никогда не рассматриваются как часть постоянного фактора (и не должны быть); все же нужно знать о них, потому что иногда (хотя и редко) они могут влиять на вещи. Например, в cpython реализация очереди с собственным приоритетом асимптотически неоптимальна (O(log(N)) скорее, чем O(1) на ваш выбор вставки или найти мин); Вы используете другую реализацию? Вероятно, нет, так как реализация C, вероятно, быстрее, и, возможно, есть другие подобные проблемы в других местах. Есть компромиссы; иногда они имеют значение, а иногда нет.
(редактировать: на этом "простое английское" объяснение заканчивается.)
Math Addenda
Для полноты, точное определение обозначения big-O следующее: f(x) ∈ O(g(x)) означает, что "f асимптотически ограничена сверху константой *g": игнорируя все ниже некоторого конечного значения x, существует постоянная такая, что |f(x)| ≤ const * |g(x)| , (Другие символы следующие: так же, как O означает ≤, Ω означает ≥. Есть строчные варианты: o означает <и ω значит>.) f(x) ∈ Ɵ(g(x)) означает оба f(x) ∈ O(g(x)) а также f(x) ∈ Ω(g(x)) (верхняя и нижняя ограничены g): существуют такие константы, что f всегда будет лежать в "полосе" между const1*g(x) а также const2*g(x) , Это самое сильное асимптотическое утверждение, которое вы можете сделать и примерно эквивалентное == , (Извините, я решил отложить упоминание символов абсолютного значения до сих пор, для ясности; особенно потому, что я никогда не видел, чтобы отрицательные значения возникали в контексте информатики.)
Люди будут часто использовать = O(...), что, возможно, является более правильной нотацией "comp-sci" и вполне законно для использования; "f = O(...)" читается как "f - порядок... / f ограничен ххх..." и рассматривается как "f - некоторое выражение, асимптотика которого...". Меня учили использовать более строгие ∈ O(...), ∈ означает "элемент" (все еще читается как прежде). O(N²) на самом деле это класс эквивалентности, то есть это набор вещей, которые мы считаем одинаковыми. В этом конкретном случае O(N²) содержит такие элементы, как { 2 N², 3 N², 1/2 N², 2 N² + log(N), - N² + N^1.9,...} и бесконечно велико, но все равно есть множество. = нотация может быть более распространенной и даже используется в работах всемирно известных компьютерных ученых. Кроме того, часто случается, что в непринужденной обстановке люди говорят O(...) когда они имеют в виду Ɵ(...); это технически верно, так как множество вещей Ɵ(exactlyThis) это подмножество O(noGreaterThanThis)... и его легче набирать.;-)
РЕДАКТИРОВАТЬ: Быстрое примечание, это почти наверняка путает нотацию Big O (которая является верхней границей) с нотацией Theta (которая является верхней и нижней границами). По моему опыту, это на самом деле типично для дискуссий в неакадемических условиях. Извиняюсь за путаницу.
В одном предложении: по мере увеличения размера вашей работы, сколько времени потребуется для ее выполнения?
Очевидно, что в качестве входных данных используются только "размер", а в качестве выходных - "затраченное время" - такая же идея применима, если вы хотите поговорить об использовании памяти и т. Д.
Вот пример, где у нас есть N футболок, которые мы хотим высушить. Мы предположим, что это невероятно быстро, чтобы получить их в положении сушки (т.е. взаимодействие человека незначительно). Конечно, это не так в реальной жизни...
Использование линии стирки снаружи: при условии, что у вас бесконечно большой задний двор, стирка высыхает за O(1) раз. Сколько бы у вас ни было, оно получит то же солнце и свежий воздух, поэтому размер не влияет на время сушки.
Использование сушилки для белья: вы кладете по 10 рубашек в каждую загрузку, а затем они заканчиваются через час. (Игнорируйте действительные цифры здесь - они не имеют значения.) Таким образом, сушка 50 рубашек занимает примерно в 5 раз больше времени, чем сушка 10 рубашек.
Помещение всего в сушильный шкаф: если мы сложим все в одну большую кучу и просто дадим общее тепло, это займет много времени, чтобы средние рубашки высохли. Я не хотел бы угадывать детали, но я подозреваю, что это по крайней мере O(N^2) - когда вы увеличиваете загрузку, время сушки увеличивается быстрее.
Одним из важных аспектов нотации "большого О" является то, что в ней не сказано, какой алгоритм будет быстрее для данного размера. Возьмите хеш-таблицу (строковый ключ, целочисленное значение) против массива пар (строка, целое число). Быстрее найти ключ в хеш-таблице или элемент в массиве на основе строки? (т. е. для массива: "найдите первый элемент, в котором строковая часть соответствует заданному ключу.") Хеш-таблицы обычно амортизируются (~= "в среднем") O(1) - после того, как они настроены, это должно занять около в то же время, чтобы найти запись в таблице 100 записей, как и в таблице записей 1,000,000. Поиск элемента в массиве (на основе содержимого, а не индекса) является линейным, т. Е. O(N) - в среднем вам придется просматривать половину записей.
Делает ли это хеш-таблицу быстрее, чем массив для поиска? Не обязательно. Если у вас очень небольшая коллекция записей, массив может быть быстрее - вы можете проверить все строки за то время, которое требуется для вычисления хеш-кода той, которую вы просматриваете. Однако по мере увеличения набора данных хеш-таблица в итоге превзойдет массив.
Big O описывает верхний предел поведения функции роста, например, время выполнения программы, когда входные данные становятся большими.
Примеры:
O (n): если я удваиваю входной размер, время выполнения удваивается
O (n2): если размер ввода удваивается, время выполнения увеличивается в четыре раза
O(log n): если размер ввода удваивается, время выполнения увеличивается на единицу
O (2n): если размер ввода увеличивается на единицу, время выполнения удваивается
Размер ввода обычно представляет собой пространство в битах, необходимое для представления ввода.
Обозначение Big O чаще всего используется программистами как приблизительная мера того, сколько времени потребуется для выполнения вычисления (алгоритма), выраженного как функция размера входного набора.
Big O полезно для сравнения того, насколько хорошо два алгоритма будут масштабироваться при увеличении количества входов.
Точнее, обозначение Big O используется для выражения асимптотического поведения функции. Это означает, как функция ведет себя, приближаясь к бесконечности.
Во многих случаях "O" алгоритма попадает в один из следующих случаев:
- O (1) - время для завершения одинаково, независимо от размера входного набора. Примером является доступ к элементу массива по индексу.
- O (Log N) - Время завершения увеличивается примерно в соответствии с log2(n). Например, 1024 элемента занимают примерно вдвое больше времени, чем 32 элемента, поскольку Log2(1024) = 10 и Log2(32) = 5. Примером является поиск элемента в двоичном дереве поиска (BST).
- O (N) - время для завершения, которое масштабируется линейно с размером входного набора. Другими словами, если вы удвоите количество элементов во входном наборе, алгоритм займет примерно вдвое больше времени. Примером является подсчет количества элементов в связанном списке.
- O (N Log N) - Время завершения увеличивается на количество элементов, умноженное на результат Log2(N). Примером этого является кучная сортировка и быстрая сортировка.
- O (N ^ 2) - Время для завершения примерно равно квадрату количества предметов. Примером этого является пузырьковая сортировка.
- O (N!) - время до завершения является факториалом входного набора. Примером этого является решение проблемы грубой силы коммивояжера.
Big O игнорирует факторы, которые не вносят существенного вклада в кривую роста функции, поскольку размер входных данных увеличивается к бесконечности. Это означает, что константы, которые добавляются или умножаются на функцию, просто игнорируются.
Big O - это просто способ "выразить" себя обычным способом: "Сколько времени / пространства требуется для запуска моего кода?".
Вы можете часто видеть O (n), O (n2), O (nlogn) и так далее, все это просто способы показать; Как меняется алгоритм?
O (n) означает, что Big O - это n, и теперь вы можете подумать: "Что такое n!?" Ну, "n" это количество элементов. Изображение, которое вы хотите найти для элемента в массиве. Вы должны смотреть на каждый элемент и как "Вы правильный элемент / предмет?" в худшем случае, элемент находится в последнем индексе, что означает, что это заняло столько же времени, сколько элементов в списке, поэтому, чтобы быть обобщенным, мы говорим: "О, эй, n - справедливое заданное количество значений!",
Таким образом, вы можете понять, что означает "n2", но чтобы быть еще более конкретным, поиграйте с мыслью, что у вас есть простой, самый простой из алгоритмов сортировки; BubbleSort. Этот алгоритм должен просматривать весь список для каждого элемента.
Мой список
- 1
- 6
- 3
Поток здесь будет:
- Сравните 1 и 6, какой самый большой? ОК 6 находится в правильном положении, двигаясь вперед!
- Сравните 6 и 3, ах, 3 меньше! Давайте переместим это, хорошо, список изменился, мы должны начать с самого начала!
Это O n2, потому что вам нужно посмотреть на все элементы в списке, есть "n" элементов. Для каждого элемента вы просматриваете все элементы еще раз, для сравнения, это также "n", поэтому для каждого элемента вы смотрите "n" раз, означая n * n = n2
Я надеюсь, что это так просто, как вы хотите.
Но помните, Big O - это просто способ испытать себя в манере времени и пространства.
Big O описывает фундаментальную масштабирующую природу алгоритма.
Существует много информации, которую Big O не сообщает вам о данном алгоритме. Он сокращает до костей и дает только информацию о масштабируемой природе алгоритма, в частности о том, как использование ресурсов (время мысли или память) алгоритма масштабируется в ответ на "размер ввода".
Рассмотрим разницу между паровым двигателем и ракетой. Это не просто разные разновидности одного и того же (как, скажем, двигатель Prius против двигателя Lamborghini), но в своей основе они представляют собой принципиально разные типы силовых установок. Паровой двигатель может быть быстрее, чем игрушечная ракета, но ни один паропоршневой двигатель не сможет достичь скорости орбитальной ракеты-носителя. Это связано с тем, что эти системы имеют различные характеристики масштабирования в зависимости от соотношения количества топлива ("использование ресурсов") для достижения заданной скорости ("размер входного сигнала").
Почему это так важно? Поскольку программное обеспечение имеет дело с проблемами, которые могут различаться по размеру в три раза. Подумайте об этом на мгновение. Соотношение между скоростью, необходимой для полета на Луну, и скоростью ходьбы человека составляет менее 10000:1, и это абсолютно незначительно по сравнению с диапазоном размеров входного программного обеспечения. И поскольку программное обеспечение может сталкиваться с астрономическим диапазоном входных размеров, существует вероятность того, что алгоритм Big O будет сложным, поскольку он имеет фундаментальную масштабирующую природу и превосходит любые детали реализации.
Рассмотрим пример канонической сортировки. Bubble-sort - это O (n2), а merge-sort - O(n log n). Допустим, у вас есть два приложения для сортировки: приложение A, которое использует пузырьковую сортировку, и приложение B, которое использует сортировку слиянием, и предположим, что при входных размерах около 30 элементов приложение A в 1000 раз быстрее, чем приложение B при сортировке. Если вам никогда не нужно сортировать более 30 элементов, то очевидно, что вы должны предпочесть приложение A, так как оно намного быстрее при таких размерах ввода. Однако, если вы обнаружите, что вам может потребоваться отсортировать десять миллионов элементов, то вы ожидаете, что приложение B на самом деле окажется в тысячи раз быстрее, чем приложение A в этом случае, полностью из-за того, как масштабируется каждый алгоритм.
Вот простой английский бестиарий, который я склонен использовать при объяснении распространенных разновидностей Биг-О
Во всех случаях предпочтите алгоритмы, расположенные выше в списке, а не в списке ниже. Однако стоимость перехода на более дорогой класс сложности значительно варьируется.
O(1):
Нет роста. Независимо от того, насколько велика проблема, вы можете решить ее за одно и то же время. Это в некоторой степени аналогично вещанию, когда для вещания на заданном расстоянии требуется одинаковое количество энергии, независимо от количества людей, которые находятся в пределах диапазона вещания.
O (log n):
Эта сложность такая же, как O(1), за исключением того, что она немного хуже. Для всех практических целей вы можете рассматривать это как очень большое постоянное масштабирование. Разница в работе между обработкой 1 тыс. И 1 млрд. Единиц составляет всего шесть раз.
O (n):
Стоимость решения проблемы пропорциональна размеру проблемы. Если ваша проблема удваивается в размерах, то стоимость решения удваивается. Поскольку большинство проблем необходимо каким-либо образом сканировать в компьютер, например, при вводе данных, чтении с диска или сетевом трафике, это обычно является доступным фактором масштабирования.
O (n log n):
Эта сложность очень похожа на O (n). Для всех практических целей, оба эквивалентны. Этот уровень сложности обычно считается масштабируемым. Путем изменения предположений некоторые O (n log n) алгоритмы могут быть преобразованы в O (n) алгоритмы. Например, ограничение размера ключей уменьшает сортировку с O (n log n) до O (n).
O (n2):
Растет как квадрат, где n - длина стороны квадрата. Это такой же темп роста, как и "сетевой эффект", когда каждый в сети может знать всех остальных в сети. Рост дорогой. Большинство масштабируемых решений не могут использовать алгоритмы с таким уровнем сложности без значительной гимнастики. Это обычно относится ко всем другим полиномиальным сложностям - O (nk) - также.
O (2n):
Не масштабируется. У вас нет надежды на решение любой нетривиальной задачи. Полезно для того, чтобы знать, чего следует избегать, и для экспертов, чтобы найти приближенные алгоритмы, которые находятся в O (nk).
Big O - это мера того, сколько времени / пространства использует алгоритм относительно размера его входных данных.
Если алгоритм равен O(n), то время / пространство будут увеличиваться с той же скоростью, что и его входные данные.
Если алгоритм равен O (n2), то время / пространство увеличиваются со скоростью его входных данных в квадрате.
и так далее.
Очень сложно измерить скорость программ, и когда мы попробуем, ответы могут быть очень сложными и заполнены исключениями и особыми случаями. Это большая проблема, потому что все эти исключения и особые случаи отвлекают и бесполезны, когда мы хотим сравнить две разные программы друг с другом, чтобы выяснить, какая из них "самая быстрая".
В результате всей этой бесполезной сложности люди пытаются описать скорость программ, используя самые маленькие и наименее сложные (математические) выражения. Эти выражения являются очень очень грубыми приближениями: хотя, если повезет, они уловят "суть", является ли часть программного обеспечения быстрой или медленной.
Поскольку они являются приблизительными, мы используем букву "О" (Big Oh) в выражении, чтобы договориться с читателем о том, что мы делаем грубое упрощение. (И чтобы никто не ошибочно считал, что выражение в любом случае точное).
Если вы прочитаете "О" как означающее "порядка" или "приблизительно", вы не ошибетесь слишком далеко. (Я думаю, что выбор Big-Oh, возможно, был попыткой юмора).
Единственное, что пытаются сделать выражения "Big-Oh", - это описать, насколько сильно программное обеспечение замедляется по мере того, как мы увеличиваем объем данных, которые должно обрабатывать программное обеспечение. Если мы удвоим объем данных, которые необходимо обработать, потребуется ли программе вдвое больше времени, чтобы завершить свою работу? Десять раз больше? На практике вы можете столкнуться с очень ограниченным числом выражений большого-ой, о которых вам нужно беспокоиться:
Хорошо:
O(1)Постоянная: программа запускается независимо от размера ввода.O(log n)Логарифмический: время выполнения программы увеличивается только медленно, даже при большом увеличении размера ввода.
Плохо:
O(n)Линейный: время выполнения программы увеличивается пропорционально размеру ввода.O(n^k)Полином: время обработки растет все быстрее и быстрее - как полиномиальная функция - с увеличением размера входных данных.
... и мерзкий
O(k^n)Экспоненциальное Время выполнения программы очень быстро увеличивается даже при умеренном увеличении размера задачи - практично обрабатывать небольшие наборы данных с помощью экспоненциальных алгоритмов.O(n!)Факториал Время выполнения программы будет больше, чем вы можете позволить себе ждать чего угодно, кроме самых маленьких и самых простых на вид наборов данных.
Что такое простое английское объяснение Big O? С как можно меньшим формальным определением и простой математикой.
Простое английское объяснение необходимости обозначения Big-O:
Когда мы программируем, мы пытаемся решить проблему. То, что мы кодируем, называется алгоритмом. Обозначение Big O позволяет нам сравнивать производительность наших алгоритмов в худшем случае стандартизированным способом. Характеристики оборудования меняются со временем, а улучшения в оборудовании могут сократить время, необходимое для выполнения алгоритмов. Но замена оборудования не означает, что наш алгоритм улучшается или совершенствуется с течением времени, так как наш алгоритм остается тем же. Таким образом, чтобы позволить нам сравнивать различные алгоритмы, чтобы определить, является ли один лучше или нет, мы используем обозначение Big O.
Простое английское объяснение того, что такое обозначение Big O:
Не все алгоритмы работают за одинаковое количество времени и могут варьироваться в зависимости от количества элементов на входе, которое мы назовем n. Основываясь на этом, мы рассматриваем худший анализ случая или верхнюю границу времени выполнения, когда n становится все больше и больше. Мы должны знать, что такое n, потому что многие из обозначений Big O ссылаются на него.
Хорошо, мои 2цента.
Big-O - скорость увеличения ресурсов, потребляемых программой, по сравнению с размером экземпляра
Ресурс: может быть общее время ЦП, может быть максимальное пространство ОЗУ. По умолчанию относится к времени процессора.
Скажем, проблема "Найти сумму",
int Sum(int*arr,int size){
int sum=0;
while(size-->0)
sum+=arr[size];
return sum;
}
задача-экземпляр = {5,10,15} ==> проблема-экземпляр-размер = 3, итерации в цикле = 3
задача-экземпляр = {5,10,15,20,25} ==> проблема-экземпляр-размер = 5 итераций в цикле = 5
При вводе размера "n" программа растет со скоростью "n" итераций в массиве. Следовательно, Big-O - это N, выраженное как O(n)
Скажем, проблема "Найти комбинацию",
void Combination(int*arr,int size)
{ int outer=size,inner=size;
while(outer -->0) {
inner=size;
while(inner -->0)
cout<<arr[outer]<<"-"<<arr[inner]<<endl;
}
}
задача-экземпляр = {5,10,15} ==> проблема-экземпляр-размер = 3, всего итераций = 3*3 = 9
задача-экземпляр = {5,10,15,20,25} ==> проблема-экземпляр-размер = 5, всего итераций = 5*5 =25
При вводе размера "n" программа растет со скоростью "n*n" итераций в массиве. Следовательно, Big-O - это N 2, выраженное как O (n 2)
Простой прямой ответ может быть:
Большой O представляет наихудшее время / пространство для этого алгоритма. Алгоритм никогда не займет больше места / времени выше этого предела. Большой O представляет сложность времени / пространства в крайнем случае.
Нотация Big O - это способ описания верхней границы алгоритма в терминах пространства или времени выполнения. N - это количество элементов в задаче (т. Е. Размер массива, количество узлов в дереве и т. Д.). Мы заинтересованы в описании времени выполнения, когда n становится большим.
Когда мы говорим, что некоторым алгоритмом является O (f (n)), мы говорим, что время выполнения (или пространство, необходимое) для этого алгоритма всегда меньше, чем некоторое постоянное время f (n).
Сказать, что бинарный поиск имеет время выполнения O (logn), значит сказать, что существует некоторая константа c, которую вы можете умножить на log (n), которая всегда будет больше времени выполнения бинарного поиска. В этом случае вы всегда будете иметь некоторый постоянный коэффициент сравнения log (n).
Другими словами, где g (n) - время выполнения вашего алгоритма, мы говорим, что g(n) = O(f(n)), когда g(n) <= c*f(n), когда n > k, где с и к некоторые константы.
" Что такое простое английское объяснение Big O? Как можно меньше формального определения и простой математики ".
Такой красивый простой и короткий вопрос, по крайней мере, заслуживает такого же короткого ответа, который студент может получить во время обучения.
Обозначение Big O просто говорит, сколько времени * алгоритм может работать в течение, только в терминах количества входных данных **.
(* в прекрасном, свободном от единицы смысле времени!)
(** что имеет значение, потому что люди всегда хотят большего, живут ли они сегодня или завтра)
Ну, что такого замечательного в обозначении Big O, если это то, что он делает?
Практически говоря, анализ Big O является настолько полезным и важным, потому что Big O прямо фокусируется на собственной сложности алгоритма и полностью игнорирует все, что является просто константой пропорциональности - например, движок JavaScript, скорость процессора, ваше интернет-соединение и все те вещи, которые быстро становятся такими же смехотворно устаревшими, как модель Т. Big O фокусируется на производительности только таким образом, который одинаково важен для людей, живущих в настоящем или в будущем.
Система обозначений Big O также освещает самый важный принцип компьютерного программирования / инжиниринга, тот факт, что все хорошие программисты вдохновляют всех думать и мечтать: единственный способ достичь результатов, выходящих за рамки медленного продвижения вперед, - это изобрести лучший способ. алгоритм
Пример алгоритма (Java):
// given a list of integers L, and an integer K
public boolean simple_search(List<Integer> L, Integer K)
{
// for each integer i in list L
for (Integer i : L)
{
// if i is equal to K
if (i == K)
{
return true;
}
}
return false;
}
Описание алгоритма:
Этот алгоритм поиска списка, элемент за элементом, ищет ключ,
Итерируя по каждому элементу в списке, если это ключ, верните True,
Если цикл завершился без поиска ключа, верните False.
Обозначения Big-O представляют верхнюю границу сложности (время, пространство, ..)
Чтобы найти Big-O на сложности времени:
Подсчитайте, сколько времени (относительно размера ввода) занимает наихудший случай:
В худшем случае: ключ не существует в списке.
Время (в худшем случае) = 4n+1
Время: O(4n+1) = O(n) | в Big-O константы игнорируются
O(n) ~ Линейный
Есть также Big-Omega, которые представляют сложность Best-Case:
Best-Case: ключ - это первая вещь.
Время (в лучшем случае) = 4
Время: Ω(4) = O(1) ~ Мгновенное \ Постоянное
Обозначение Big O - это способ описания того, как быстро алгоритм будет работать при произвольном числе входных параметров, которые мы назовем "n". Это полезно в компьютерных науках, потому что разные машины работают на разных скоростях, и просто сказать, что алгоритм занимает 5 секунд, мало что вам скажет, потому что, пока вы работаете в системе с процессором с тактовой частотой 4,5 ГГц, я могу работать 15-летняя система 800 МГц, которая может занять больше времени независимо от алгоритма. Поэтому вместо того, чтобы указывать, насколько быстро алгоритм работает с точки зрения времени, мы говорим, насколько быстро он работает с точки зрения количества входных параметров, или "n". Описывая алгоритмы таким образом, мы можем сравнивать скорости алгоритмов без необходимости учитывать скорость самого компьютера.
Большой О
f(x) = O (g(x)), когда x переходит к a (например, a = +∞), означает, что существует функция k такая, что:
f(x) = k(x)g(x)
k ограничено в некоторой окрестности a (если a = +∞, это означает, что существуют числа N и M такие, что для каждого x> N, |k(x) |
Другими словами, на простом английском языке: f(x) = O (g(x)), x → a, означает, что в окрестности a f разлагается в произведение g на некоторую ограниченную функцию.
Маленький о
Кстати, вот для сравнения определение малого o.
f(x) = o (g(x)), когда x означает, что существует функция k такая, что:
f(x) = k(x)g(x)
k(x) переходит к 0, когда x переходит к a.
Примеры
sin x = O (x), когда x → 0.
sin x = O (1), когда x → + ∞,
x2 + x = O (x), когда x → 0,
x2 + x = O (x2), когда x → + ∞,
ln (x) = o (x) = O (x), когда x → +∞.
Внимание! Запись со знаком равенства "=" использует "поддельное равенство": верно, что o (g (x)) = O (g (x)), но неверно, что O (g (x)) = o (g (Икс)). Точно так же можно написать "ln(x) = o(x), когда x → +∞", но формула "o(x) = ln(x)" не имеет смысла.
Больше примеров
O (1) = O (n) = O (n2), когда n → +∞ (но не наоборот, равенство "фальшивое"),
O (n) + O (n2) = O (n2) при n → + ∞
O (O (n2)) = O (n2) при n → + ∞
O (n2) O (n3) = O (n5) при n → + ∞
Вот статья в Википедии: https://en.wikipedia.org/wiki/Big_O_notation
Вы хотите знать все, что нужно знать о большой O? Я тоже.
Поэтому, чтобы говорить о большом О, я буду использовать слова, в которых есть только один удар. Один звук на слово. Маленькие слова быстрые. Вы знаете эти слова, и я тоже. Мы будем использовать слова с одним звуком. Они маленькие. Я уверен, что вы будете знать все слова, которые мы будем использовать!
Теперь давайте поговорим о работе. Большую часть времени я не люблю работу. Тебе нравится работать? Это может быть тот случай, что вы делаете, но я уверен, что нет.
Я не люблю ходить на работу. Я не люблю проводить время на работе. Если бы у меня был свой путь, я бы просто хотел играть и делать забавные вещи. Ты чувствуешь то же самое, что и я?
Время от времени я должен идти на работу. Это грустно, но верно. Поэтому, когда я на работе, у меня есть правило: я стараюсь выполнять меньше работы. Как близко к работе, как я могу. Тогда я пойду играть!
Итак, вот большая новость: большой О может помочь мне не работать! Я могу играть больше времени, если я знаю большой О. Меньше работы, больше игры! Это то, что большой О помогает мне сделать.
Теперь у меня есть работа. У меня есть этот список: один, два, три, четыре, пять, шесть. Я должен добавить все вещи в этом списке.
Вау, я ненавижу работу. Ну да ладно, я должен это сделать. Итак, я иду.
Один плюс два - это три... плюс три - это шесть... а четыре - это... я не знаю. Я потерялся. Это слишком сложно для меня сделать в моей голове. Меня не очень волнует такая работа.
Так что давайте не будем делать работу. Давай ты и я просто подумаем, как это тяжело. Сколько работы мне нужно сделать, чтобы добавить шесть цифр?
Ну что ж, посмотрим. Я должен добавить одно и два, а затем добавить это к трем, а затем добавить это к четырем... В общем, я считаю шесть добавлений. Я должен сделать шесть добавок, чтобы решить это.
Вот большая буква О, чтобы сказать нам, насколько сложна эта математика.
Большой О говорит: мы должны сделать шесть добавок, чтобы решить эту проблему. Одно добавление, для каждой вещи от одного до шести. Шесть маленьких кусочков работы... каждый кусочек работы - это одно дополнение.
Ну, я не буду делать работу, чтобы добавить их сейчас. Но я знаю, как это будет сложно. Было бы шесть добавляет.
О нет, теперь у меня есть больше работы. Sheesh. Кто делает такие вещи?!
Теперь они просят меня прибавить от одного до десяти! Зачем мне это делать? Я не хотел добавлять один к шести. Добавить от одного до десяти... ну... это было бы еще сложнее!
Насколько сложнее это будет? Сколько еще работы мне нужно сделать? Нужно ли больше или меньше шагов?
Ну, я думаю, мне нужно сделать десять добавлений... по одному на каждую вещь от одного до десяти. Десять больше шести. Мне пришлось бы работать намного больше, чтобы добавить от одного до десяти, чем от одного до шести!
Я не хочу добавлять прямо сейчас. Я просто хочу подумать о том, как трудно это добавить. И, надеюсь, играть так скоро, как смогу.
Чтобы добавить от одного до шести, это некоторая работа. Но вы видите, добавить от одного до десяти, это больше работы?
Большой О - твой друг и мой. Big O помогает нам думать о том, сколько работы мы должны сделать, чтобы мы могли планировать. И, если мы дружим с большим О, он может помочь нам выбрать работу, которая не так сложна!
Теперь мы должны сделать новую работу. О нет. Мне вообще не нравится эта работа.
Новая работа: добавить все вещи от одного до n.
Подождите! Что это н? Я пропустил это? Как я могу добавить от одного к п, если вы не говорите мне, что п?
Ну, я не знаю, что это такое. Мне не сказали. Были ли вы? Нет? Ну что ж. Поэтому мы не можем делать работу. Уф.
Но хотя мы не будем делать работу сейчас, мы можем догадаться, насколько это будет сложно, если бы мы знали n. Мы должны были бы сложить n вещей, верно? Конечно!
Теперь здесь идет большой O, и он скажет нам, как тяжело эта работа. Он говорит: добавить все от одного к N, один за другим, есть O(n). Чтобы добавить все эти вещи, [я знаю, я должен добавить n раз.][1] Это большой O! Он говорит нам, как тяжело делать какую-то работу.
Для меня я думаю о большом О как о большом, медленном, боссовом человеке. Он думает о работе, но он этого не делает. Он может сказать: "Эта работа быстрая". Или он может сказать: "Эта работа такая медленная и тяжелая!" Но он не делает работу. Он просто смотрит на работу, а затем говорит нам, сколько времени это может занять.
Я забочусь о большом О. Почему? Я не люблю работать! Никто не любит работать. Вот почему мы все любим большой O! Он говорит нам, как быстро мы можем работать. Он помогает нам думать о том, как тяжело работать.
О, больше работы. Теперь давайте не будем делать работу. Но давайте составим план, шаг за шагом.
Они дали нам колоду из десяти карт. Они все перепутаны: семь, четыре, два, шесть… совсем не прямые. А теперь... наша работа - сортировать их.
Ergh. Это звучит как большая работа!
Как мы можем отсортировать эту колоду? У меня есть план.
Я буду смотреть на каждую пару карт, пара за парой, через колоду, от первой до последней. Если первая карта в одной паре большая, а следующая в этой паре маленькая, я поменяю их местами. Иначе, я иду к следующей паре, и так далее, и так далее... и скоро колода готова.
Когда колода закончена, я спрашиваю: обменял ли я карты в этом проходе? Если это так, я должен сделать все это еще раз, сверху.
В какой-то момент, в какое-то время перестановок не будет, и наша колода будет готова. Так много работы!
Ну, а сколько это будет стоить, чтобы отсортировать карточки по этим правилам?
У меня есть десять карт. И большую часть времени - то есть, если мне не везет - я должен пройти всю колоду до десяти раз, с помощью до десяти обменов карт каждый раз через колоду.
Большой О, помоги мне!
Входит большой О и говорит: для колоды из n карт сортировка будет выполнена за O(N в квадрате).
Почему он говорит n в квадрате?
Ну, вы знаете, n в квадрате - это n раз n. Теперь я понял: n карт проверено, вплоть до того, что может быть n раз в колоде. Это две петли, каждая из которых имеет n шагов. Это большая работа, которую предстоит сделать. Конечно, много работы!
Теперь, когда большой O говорит, что ему потребуется O (n в квадрате), он не означает, что n в квадрате добавляет на носу. Это может быть немного меньше, в некоторых случаях. Но в худшем случае для сортировки колоды потребуется около n шагов в квадрате.
Теперь здесь, где большой О наш друг.
Большой O указывает на это: когда n становится большим, когда мы сортируем карточки, работа становится НАМНОГО БОЛЬШЕ тяжелее, чем старая работа "просто добавь эти вещи". Откуда нам это знать?
Что ж, если n становится действительно большим, нам все равно, что мы можем добавить к n или n в квадрате.
Для больших n квадрат n больше, чем n.
Big O говорит нам, что сортировать вещи сложнее, чем добавлять вещи. O(n в квадрате) больше, чем O (n) для больших n. Это означает: если n становится действительно большим, сортировка смешанной колоды из n вещей ДОЛЖНА занять больше времени, чем просто добавление n смешанных вещей.
Big O не решает работу за нас. Большой О говорит нам, как тяжела работа.
У меня есть колода карт. Я их отсортировал. Вы помогли Благодарю.
Есть ли более быстрый способ сортировки карт? Может ли большой О помочь нам?
Да, есть более быстрый путь! На обучение уходит некоторое время, но оно работает... и работает довольно быстро. Вы тоже можете попробовать, но не торопитесь с каждым шагом и не теряйте своего места.
В этом новом способе сортировки колоды мы не проверяем пары карт, как мы делали это недавно. Вот ваши новые правила сортировки этой колоды:
Первый: я выбираю одну карту в той части колоды, над которой мы сейчас работаем. Вы можете выбрать один для меня, если хотите. (В первый раз, когда мы делаем это, "часть колоды, над которой мы сейчас работаем", это, конечно, вся колода.)
Два: я раскладываю колоду на той карте, которую вы выбрали. Что это за сплай; как мне выложить? Ну, я иду от стартовой карты вниз, один за другим, и ищу карту, которая выше, чем сплайс-карта.
Третье: я иду от конечной карты вверх и ищу карту ниже, чем сплайс-карта.
Найдя эти две карты, я поменяю их местами и продолжаю искать другие карты для обмена. То есть я возвращаюсь ко второму шагу и вставляю карту, которую вы выбрали, еще немного.
В какой-то момент этот цикл (от двух до трех) закончится. Он заканчивается, когда обе половины этого поиска встречаются у сплайс-карты. Затем мы только что добавили колоду с картой, которую вы выбрали в первом шаге. Теперь все карты ближе к началу находятся ниже, чем сплайс карты; и карты ближе к концу находятся выше, чем сплайс карты. Классный трюк!
Четыре (и это самое интересное): у меня сейчас две маленькие колоды: одна ниже, чем сплайс-карта, а другая - больше. Теперь я иду к первому шагу на каждой маленькой колоде! То есть я начинаю с первого шага на первой маленькой колоде, а когда эта работа закончена, я начинаю с первого шага на следующей маленькой колоде.
Я разбиваю колоду на части и сортирую каждую часть, более мелкую и более маленькую, и в какой-то момент мне больше нечем заняться. Теперь это может показаться медленным, со всеми правилами. Но поверьте мне, это совсем не медленно. Это гораздо меньше работы, чем первый способ сортировки вещей!
Как называется этот вид? Это называется Быстрая сортировка! Этот вид был сделан человеком по имени CAR Hoare, и он назвал это Quick Sort. Быстрая сортировка привыкает все время!
Быстрая сортировка разбивает большие колоды на маленькие. То есть он разбивает большие задачи на маленькие.
Хммм. Там может быть правило, я думаю. Чтобы сделать большие задачи маленькими, разбейте их.
Этот вид довольно быстрый. Как быстро? Большой O говорит нам: этот вид требует O(n log n) работы, в среднем.
Это более или менее быстро, чем первый сорт? Большой О, пожалуйста, помогите!
Первый сорт был O (n в квадрате). Но Быстрая сортировка - это O(n log n). Вы знаете, что n log n меньше n в квадрате, для больших n, верно? Ну, вот как мы знаем, что быстрая сортировка быстро!
Если вам нужно отсортировать колоду, как лучше? Ну, вы можете делать то, что вы хотите, но я бы выбрал быструю сортировку.
Почему я выбираю быструю сортировку? Я не люблю работать, конечно! Я хочу, чтобы работа была выполнена, как только я смогу это сделать.
Откуда я знаю, что быстрая сортировка - это меньше работы? Я знаю, что O(n log n) меньше, чем O (n в квадрате). O более маленькие, поэтому быстрая сортировка - меньше работы!
Теперь вы знаете моего друга, Big O. Он помогает нам выполнять меньше работы. И если ты знаешь большой О, ты тоже можешь выполнять меньше работы!
Вы узнали все это со мной! Ты такой умный! Спасибо вам большое!
Теперь, когда работа сделана, поехали играть!
[1]: Есть способ обмануть и добавить все вещи от одного до n, все за один раз. Какой-то ребенок по имени Гаусс узнал об этом, когда ему было восемь лет. Я не такой умный, поэтому не спрашивайте меня, как он это сделал.
Не уверен, что я продолжаю вносить свой вклад в эту тему, но все же думал, что поделюсь: однажды я обнаружил, что в этом блоге есть несколько весьма полезных (хотя и очень простых) объяснений и примеров по Big O:
Посредством примеров это помогло получить базовые знания в моем черепахоподобном черепе, так что я думаю, что это 10-минутное чтение, которое поможет вам двигаться в правильном направлении.
У меня есть более простой способ понять сложность времени, которую он чаще всего использует для вычисления сложности времени, - это обозначение Big O. Это устраняет все постоянные факторы, так что время работы можно оценить по отношению к N, когда N приближается к бесконечности. В общем, вы можете думать об этом так:
statement;
Постоянно. Время выполнения оператора не изменится по отношению к N
for ( i = 0; i < N; i++ )
statement;
Является линейным. Время работы цикла прямо пропорционально N. Когда N удваивается, то же самое происходит и время работы.
for ( i = 0; i < N; i++ )
{
for ( j = 0; j < N; j++ )
statement;
}
Является квадратичным Время работы двух петель пропорционально квадрату N. Когда N удваивается, время работы увеличивается на N * N.
while ( low <= high )
{
mid = ( low + high ) / 2;
if ( target < list[mid] )
high = mid - 1;
else if ( target > list[mid] )
low = mid + 1;
else break;
}
Логарифмический Время выполнения алгоритма пропорционально числу делений N на 2. Это происходит потому, что алгоритм делит рабочую область пополам с каждой итерацией.
void quicksort ( int list[], int left, int right )
{
int pivot = partition ( list, left, right );
quicksort ( list, left, pivot - 1 );
quicksort ( list, pivot + 1, right );
}
Есть N * log (N). Время выполнения состоит из N циклов (итеративных или рекурсивных), которые являются логарифмическими, поэтому алгоритм представляет собой комбинацию линейных и логарифмических.
В общем, выполнение чего-либо с каждым элементом в одном измерении является линейным, выполнение чего-либо с каждым элементом в двух измерениях является квадратичным, а деление рабочей области пополам - логарифмическим. Существуют и другие меры Big O, такие как кубическая, экспоненциальная и квадратный корень, но они не так часто встречаются. Обозначение Big O описывается как O (), где есть мера. Алгоритм быстрой сортировки будет описан как O ( N * log ( N)).
Примечание. Ничто из этого не учитывает показатели наилучшего, среднего и наихудшего вариантов. У каждого будет своя нотация Big O. Также обратите внимание, что это ОЧЕНЬ упрощенное объяснение. Big O является наиболее распространенным, но он также более сложный, что я показал. Есть и другие обозначения, такие как большая омега, маленькая буква o и большая тэта. Вы, вероятно, не встретите их вне курса анализа алгоритма.
- Смотрите больше на: Здесь
Что такое простое английское объяснение обозначения "Big O"?
Очень быстрое примечание:
О в "Большом О" называется "Порядком"(или, точнее, "Порядком")
чтобы вы могли буквально понять, что он используется для заказа чего-то, чтобы сравнить их.
"Большой О" делает две вещи:
- Оценивает, сколько шагов метода применяется вашим компьютером для выполнения задачи.
- Облегчить процесс сравнения с другими, чтобы определить, хорошо это или нет?
- "Big O 'достигает двух вышеупомянутых стандартов
Notations,
Есть семь наиболее часто используемых обозначений
- O(1) означает, что ваш компьютер выполняет задание с
1шаг, отлично, заказал №1 - O (logN) означает, что ваш компьютер завершил задачу
logNшаги, хорошо, заказал № 2 - O (N), завершить задачу с
Nшаги, его ярмарка, приказ № 3 - O (NlogN), завершает задачу
O(NlogN)шаги, это не хорошо, Приказ № 4 - O (N ^ 2), выполни задачу
N^2шаги, это плохо, приказ № 5 - O (2 ^ N), выполни задачу
2^Nшаги, это ужасно, Приказ № 6 - O (N!), Выполни задачу
N!шаги, это ужасно, Приказ № 7
- O(1) означает, что ваш компьютер выполняет задание с
Предположим, вы получили обозначение O(N^2) Вы не только понимаете, что метод выполняет N*N шагов для выполнения задачи, но и видите, что O(NlogN) из своего рейтинга.
Пожалуйста, обратите внимание на порядок в конце строки, просто для вашего лучшего понимания. Существует более 7 обозначений, если учтены все возможности.
В CS набор шагов для выполнения задачи называется алгоритмами.
В терминологии нотация Big O используется для описания производительности или сложности алгоритма.
Кроме того, Big O устанавливает наихудший случай или измеряет верхние границы.
Вы могли бы обратиться к Big-Ω (Big-Omega) для лучшего случая.
Big-Ω (Big-Omega) обозначение (статья) | Ханская академия
Резюме
"Большой O" описывает производительность алгоритма и оценивает его.или обращайтесь к нему формально, "Большой О" классифицирует алгоритмы и стандартизирует процесс сравнения.
Предположим, мы говорим об алгоритме A, который должен что-то делать с набором данных размером n.
затем O( <some expression X involving n> ) в простом английском означает:
Если вам не повезло при выполнении A, может потребоваться выполнение X(n) операций.
Как это случается, есть определенные функции (представьте их как реализации X(n)), которые обычно встречаются довольно часто. Они хорошо известны и легко сравнимы (примеры: 1, Log N, N, N^2, N!, так далее..)
Сравнивая их, когда речь идет об А и других алгоритмах, легко ранжировать алгоритмы по количеству операций, которые они могут (в худшем случае) выполнить.
В целом, нашей целью будет найти или структурировать алгоритм A таким образом, чтобы он имел функцию X(n) который возвращает как можно меньшее число.
Скажем, вы заказываете "Гарри Поттер: полная 8-пленочная коллекция [Blu-ray]" от Amazon и загружаете ту же коллекцию фильмов онлайн одновременно. Вы хотите проверить, какой метод быстрее. Доставка занимает почти день, а загрузка завершена примерно на 30 минут раньше. Большой! Так что это жесткая гонка.
Что если я закажу несколько Blu-ray фильмов, таких как "Властелин колец", "Сумерки", "Трилогия Темного рыцаря" и т. Д., И загружу все фильмы онлайн одновременно? На этот раз доставка все еще занимает один день, но онлайн-загрузка занимает 3 дня. Для покупок в Интернете количество купленного товара (входной) не влияет на время доставки. Выход постоянный. Мы называем это O(1).
Для загрузки через Интернет время загрузки прямо пропорционально размеру файла фильма (входной). Мы называем это O(n).
Из экспериментов мы знаем, что онлайн-магазины масштабируются лучше, чем онлайн-загрузка. Очень важно понимать большие обозначения O, потому что это помогает вам анализировать масштабируемость и эффективность алгоритмов.
Примечание. Обозначение Big O представляет собой наихудший сценарий алгоритма. Предположим, что O(1) и O(n) являются сценариями наихудшего случая в приведенном выше примере.
Ссылка: http://carlcheo.com/compsci
Если у вас есть подходящее понятие бесконечности в вашей голове, то есть очень краткое описание:
Обозначение Big O говорит о стоимости решения бесконечно большой задачи.
И, кроме того
Постоянные факторы незначительны
Если вы обновитесь до компьютера, который может запустить ваш алгоритм в два раза быстрее, то большая буква O этого не заметит. Постоянные улучшения фактора слишком малы, чтобы их можно было заметить в шкале, с которой работает большая запись O. Обратите внимание, что это преднамеренная часть дизайна больших обозначений O.
Хотя можно обнаружить что-то "больше", чем постоянный фактор.
Если вы заинтересованы в выполнении вычислений, размер которых достаточно велик, чтобы их можно было считать приблизительно бесконечными, тогда большие обозначения O - это примерно стоимость решения вашей проблемы.
Если вышеупомянутое не имеет смысла, то у вас нет совместимого интуитивного понятия бесконечности в вашей голове, и вы, вероятно, должны игнорировать все вышеперечисленное; единственный способ, которым я знаю, чтобы сделать эти идеи строгими или объяснить их, если они еще не являются интуитивно полезными, - это сначала научить вас большому O-обозначению или чему-то подобному. (хотя, как только вы хорошо поймете большие обозначения O в будущем, возможно, стоит пересмотреть эти идеи)
Определение:- Big O нотация - это нотация, которая говорит о том, как будет работать производительность алгоритма, если ввод данных увеличивается.
Когда мы говорим об алгоритмах, есть 3 важных столпа ввода, вывода и обработки алгоритма. Big O - это символьная нотация, которая говорит, что при увеличении ввода данных скорость работы алгоритма будет изменяться.
Я бы посоветовал вам посмотреть это видео на YouTube, которое подробно объясняет Big O Notation с примерами кода.
Например, предположим, что алгоритм занимает 5 записей, а время, необходимое для его обработки, составляет 27 секунд. Теперь, если мы увеличим записи до 10, алгоритм займет 105 секунд.
Проще говоря, время занимает квадрат числа записей. Мы можем обозначить это через O (n ^ 2). Это символическое представление называется обозначением Big O.
Теперь обратите внимание, что во входных единицах может быть что угодно, это могут быть байты, количество битов записей, производительность может быть измерена в любой единице, например секундах, минутах, днях и т. Д. Так что это не точная единица, а отношения.
Например, посмотрите на приведенную ниже функцию "Function1", которая принимает коллекцию и выполняет обработку первой записи. Теперь для этой функции производительность будет одинаковой, независимо от того, вы поставили 1000, 10000 или 100000 записей. Таким образом, мы можем обозначить это через O (1).
void Function1(List<string> data)
{
string str = data[0];
}
Теперь посмотрите на функцию ниже "Function2()". В этом случае время обработки будет увеличиваться с увеличением количества записей. Мы можем обозначить производительность этого алгоритма, используя O (n).
void Function2(List<string> data)
{
foreach(string str in data)
{
if (str == "shiv")
{
return;
}
}
}
Когда мы видим обозначение Big O для любого алгоритма, мы можем классифицировать их по трем категориям производительности:
- Журнал и постоянная категория: - Любой разработчик хотел бы видеть производительность своего алгоритма в этой категории.
- Линейный: - Разработчик не захочет видеть алгоритмы в этой категории, пока не останется последний вариант или единственный вариант.
- Экспоненциальный: - Это то место, где мы не хотим видеть наши алгоритмы, и необходима доработка.
Поэтому, взглянув на нотацию Big O, мы классифицируем хорошие и плохие зоны для алгоритмов.
Я бы порекомендовал вам посмотреть это 10-минутное видео, в котором обсуждается Big O с примером кода.
Самый простой способ посмотреть на это (простым английским языком)
Мы пытаемся увидеть, как количество входных параметров влияет на время работы алгоритма. Если время выполнения вашего приложения пропорционально количеству входных параметров, то оно называется Big O of n.
Вышеприведенное утверждение - хорошее начало, но не совсем верно.
Более точное объяснение (математическое)
предполагать
n= количество входных параметров
T(n)= Фактическая функция, которая выражает время работы алгоритма как функцию от n
с = константа
f(n)= приближенная функция, которая выражает время работы алгоритма как функцию от n
Тогда, что касается Big O, аппроксимация f (n) считается достаточно хорошей, если выполняется условие, указанное ниже.
lim T(n) ≤ c×f(n)
n→∞
Уравнение читается, когда n приближается к бесконечности, T of n меньше или равно c раз f от n.
В большой нотации это записывается как
T(n)∈O(n)
Это читается как T из n в большом O из n.
Вернуться на английский
Исходя из приведенного выше математического определения, если вы говорите, что ваш алгоритм представляет собой Big O из n, это означает, что он является функцией от n (числа входных параметров) или быстрее. Если ваш алгоритм Big O из n, то он также автоматически является квадратом Big O из n.
Большое O из n означает, что мой алгоритм работает по крайней мере так же быстро, как этот. Вы не можете смотреть на обозначение Big O вашего алгоритма и говорить, что он медленный. Вы можете только сказать, что это быстро.
Проверьте это для видео-учебника по Big O от Калифорнийского университета в Беркли. На самом деле это простая концепция. Если вы услышите, как профессор Шивчук (он же учитель уровня Бога) объясняет это, вы скажете: "О, вот и все!".
Предисловие
алгоритм: процедура / формула для решения задачи
Как анализировать алгоритмы и как мы можем сравнивать алгоритмы друг с другом?
Пример: вас и друга просят создать функцию суммирования чисел от 0 до N. Вы получаете f(x), а ваш друг - g(x). Обе функции имеют одинаковый результат, но разные алгоритмы. Чтобы объективно сравнить эффективность алгоритмов, мы используем обозначение Big-O.
Обозначение Big-O: описывает, как быстро будет расти время выполнения относительно ввода, когда входное значение будет произвольно большим.
3 ключевых выноса:
- Сравните, насколько быстро растет время выполнения, НЕ сравнивайте точное время выполнения (зависит от аппаратного обеспечения).
- Относится только к росту времени выполнения относительно ввода (n)
- Поскольку n становится произвольно большим, сфокусируйтесь на терминах, которые будут расти быстрее всего, когда n становится большим (думаю, бесконечность) АКА- асимптотический анализ
Сложность пространства: кроме сложности времени, мы также заботимся о сложности пространства (сколько памяти / пространства использует алгоритм). Вместо того, чтобы проверять время операций, мы проверяем размер выделения памяти.
Я нашел действительно отличное объяснение о большой нотации, особенно для человека, который не слишком увлекается математикой.
https://rob-bell.net/2009/06/a-beginners-guide-to-big-o-notation/
Обозначение Big O используется в компьютерных науках для описания производительности или сложности алгоритма. Big O конкретно описывает сценарий наихудшего случая и может использоваться для описания требуемого времени выполнения или используемого пространства (например, в памяти или на диске) алгоритмом.
Любой, кто читает "Программирование жемчужин" или любые другие книги по информатике и не имеет оснований по математике, попадет в стену, когда достигнет глав, в которых упоминается O(N log N) или другой, казалось бы, безумный синтаксис. Надеюсь, эта статья поможет вам понять основы Big O и логарифмов.
Будучи первым программистом и вторым математиком (или, может быть, третьим или четвертым), я обнаружил, что наилучшим способом для полного понимания Big O было создание некоторых примеров в коде. Итак, ниже приведены некоторые общие порядки роста, а также описания и примеры, где это возможно.
O (1)
O (1) описывает алгоритм, который всегда будет выполняться в одно и то же время (или пространство) независимо от размера набора входных данных.
bool IsFirstElementNull(IList<string> elements) { return elements[0] == null; } O(N)НА)
O (N) описывает алгоритм, производительность которого будет расти линейно и прямо пропорционально размеру набора входных данных. Пример ниже также демонстрирует, как Big O поддерживает сценарий производительности в худшем случае; соответствующая строка может быть найдена во время любой итерации цикла for, и функция вернется рано, но нотация Big O всегда будет принимать верхний предел, в котором алгоритм будет выполнять максимальное количество итераций.
bool ContainsValue(IList<string> elements, string value) { foreach (var element in elements) { if (element == value) return true; } return false; }O (N2)
O (N2) представляет алгоритм, производительность которого прямо пропорциональна квадрату размера входного набора данных. Это распространено в алгоритмах, которые включают вложенные итерации по набору данных. Более глубокие вложенные итерации приведут к O (N3), O (N4) и т. Д.
bool ContainsDuplicates(IList<string> elements) { for (var outer = 0; outer < elements.Count; outer++) { for (var inner = 0; inner < elements.Count; inner++) { // Don't compare with self if (outer == inner) continue; if (elements[outer] == elements[inner]) return true; } } return false; }O (2N)
O (2N) обозначает алгоритм, рост которого удваивается с каждым дополнением к набору входных данных. Кривая роста функции O (2N) имеет экспоненциальный характер: она начинается очень неглубоко, а затем возрастает метеоритно. Примером функции O (2N) является рекурсивный расчет чисел Фибоначчи:
int Fibonacci(int number) { if (number <= 1) return number; return Fibonacci(number - 2) + Fibonacci(number - 1); }Логарифмы
Логарифмы немного сложнее объяснить, поэтому я буду использовать общий пример:
Бинарный поиск - это метод, используемый для поиска отсортированных наборов данных. Он работает путем выбора среднего элемента набора данных, по сути, медианы, и сравнивает его с целевым значением. Если значения совпадают, это вернет успех. Если целевое значение выше, чем значение элемента датчика, он возьмет верхнюю половину набора данных и выполнит ту же операцию с ним. Аналогично, если целевое значение ниже, чем значение элемента зонда, оно выполнит операцию с нижней половиной. Он будет продолжать делить набор данных пополам на каждую итерацию до тех пор, пока не будет найдено значение или пока он больше не сможет разделить набор данных.
Этот тип алгоритма описывается как O(log N). Итеративное деление пополам наборов данных, описанных в примере бинарного поиска, создает кривую роста, которая достигает пика в начале и медленно сглаживается по мере увеличения размера наборов данных, например, для набора входных данных, содержащего 10 элементов, требуется одна секунда, набор данных содержит 100 элементов, занимает две секунды, а набор данных, содержащий 1000 элементов, - три секунды. Удвоение размера набора входных данных мало влияет на его рост, так как после одной итерации алгоритма набор данных будет уменьшен вдвое и, следовательно, наравне с набором входных данных, равным половине размера. Это делает такие алгоритмы, как бинарный поиск, чрезвычайно эффективными при работе с большими наборами данных.