Удалить повторяющиеся элементы списка, сохраняя порядок появления
Я делаю плоские списки с 10^6 до 10^7 действительными числами, и некоторые из них повторяются.
Мне нужно удалить повторяющиеся экземпляры, сохраняя только первое вхождение и не изменяя порядок списка.
Ключевым моментом здесь является эффективность, так как у меня много списков для обработки.
Пример (подделка):
Входные данные:
{.8, .3 , .8, .5, .3, .6}
Желаемый вывод
{.8, .3, .5, .6}
В сторону примечание
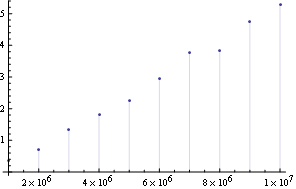
Удаление повторяющихся элементов с помощью Union (без сохранения порядка) дает в ноутбуке моего бедняка:
DiscretePlot[a = RandomReal[10, i]; First@Timing@Union@a, {i, 10^6 Range@10}]
3 ответа
Ты хочешь DeleteDuplicates, который сохраняет порядок списка:
In[13]:= DeleteDuplicates[{.8, .3, .8, .5, .3, .6}]
Out[13]= {0.8, 0.3, 0.5, 0.6}
Это было добавлено в Mathematica 7.0.
Не конкурировать с другими ответами, но я просто не мог не поделиться Compile решение на основе. Решение основано на построении бинарного дерева поиска, а затем проверяет для каждого числа в списке, является ли его индекс в списке тем, который используется при построении b-дерева. Если да, то это исходный номер, если нет - это дубликат. Что делает это решение интересным для меня, так это то, что оно показывает способ эмулировать "передачу по ссылке" Compile, Дело в том, что, если мы встроим скомпилированные функции в другие скомпилированные функции (и это может быть достигнуто с помощью опции "InlineCompiledFunctions"), мы можем ссылаться во внутренних функциях на переменные, определенные во внешней области действия функции (из-за того, как работает встраивание), Это не настоящий переход по ссылке, но он по-прежнему позволяет комбинировать функции из меньших блоков без потери эффективности (это больше в духе макро-расширения). Я не думаю, что это задокументировано, и не знаю, останется ли это в будущих версиях. В любом случае, вот код:
(* A function to build a binary tree *)
Block[{leftchildren , rightchildren},
makeBSearchTree =
Compile[{{lst, _Real, 1}},
Module[{len = Length[lst], ctr = 1, currentRoot = 1},
leftchildren = rightchildren = Table[0, {Length[lst]}];
For[ctr = 1, ctr <= len, ctr++,
For[currentRoot = 1, lst[[ctr]] != lst[[currentRoot]],(*
nothing *),
If[lst[[ctr]] < lst[[currentRoot]],
If[leftchildren[[currentRoot]] == 0,
leftchildren[[currentRoot]] = ctr;
Break[],
(* else *)
currentRoot = leftchildren[[currentRoot]] ],
(* else *)
If[rightchildren[[currentRoot]] == 0,
rightchildren[[currentRoot]] = ctr;
Break[],
(* else *)
currentRoot = rightchildren[[currentRoot]]]]]];
], {{leftchildren, _Integer, 1}, {rightchildren, _Integer, 1}},
CompilationTarget -> "C", "RuntimeOptions" -> "Speed",
CompilationOptions -> {"ExpressionOptimization" -> True}]];
(* A function to query the binary tree and check for a duplicate *)
Block[{leftchildren , rightchildren, lst},
isDuplicate =
Compile[{{index, _Integer}},
Module[{currentRoot = 1, result = True},
While[True,
Which[
lst[[index]] == lst[[currentRoot]],
result = index != currentRoot;
Break[],
lst[[index]] < lst[[currentRoot]],
currentRoot = leftchildren[[currentRoot]],
True,
currentRoot = rightchildren[[currentRoot]]
]];
result
],
{{leftchildren, _Integer, 1}, {rightchildren, _Integer,
1}, {lst, _Real, 1}},
CompilationTarget -> "C", "RuntimeOptions" -> "Speed",
CompilationOptions -> {"ExpressionOptimization" -> True}
]];
(* The main function *)
Clear[deldup];
deldup =
Compile[{{lst, _Real, 1}},
Module[{len = Length[lst], leftchildren , rightchildren ,
nodup = Table[0., {Length[lst]}], ndctr = 0, ctr = 1},
makeBSearchTree[lst];
For[ctr = 1, ctr <= len, ctr++,
If[! isDuplicate [ctr],
++ndctr;
nodup[[ndctr]] = lst[[ctr]]
]];
Take[nodup, ndctr]], CompilationTarget -> "C",
"RuntimeOptions" -> "Speed",
CompilationOptions -> {"ExpressionOptimization" -> True,
"InlineCompiledFunctions" -> True,
"InlineExternalDefinitions" -> True}];
Вот несколько тестов:
In[61]:= intTst = N@RandomInteger[{0,500000},1000000];
In[62]:= (res1 = deldup[intTst ])//Short//Timing
Out[62]= {1.141,{260172.,421188.,487754.,259397.,<<432546>>,154340.,295707.,197588.,119996.}}
In[63]:= (res2 = Tally[intTst,Equal][[All,1]])//Short//Timing
Out[63]= {0.64,{260172.,421188.,487754.,259397.,<<432546>>,154340.,295707.,197588.,119996.}}
In[64]:= res1==res2
Out[64]= True
Не так быстро, как Tally версия, но также Equal - и, как я уже сказал, моей целью было проиллюстрировать интересную (IMO) технику.
Для версий Mathematica до 7 и для общего интереса, вот несколько способов реализации функции UnsortedUnion (то есть DeleteDuplicates). Они собраны из справочных документов и MathGroup. Они были настроены так, чтобы принимать несколько списков, которые затем объединяются, по аналогии с Union.
Для Mathematica 4 или ранее
UnsortedUnion = Module[{f}, f[y_] := (f[y] = Sequence[]; y); f /@ Join@##] &
Для Mathematica 5
UnsortedUnion[x__List] := Reap[Sow[1, Join@x], _, # &][[2]]
Для Mathematica 6
UnsortedUnion[x__List] := Tally[Join@x][[All, 1]]
От Леонида Шифрина для Mathematica 3+ (?)
unsortedUnion[x_List] := Extract[x, Sort[Union[x] /. Dispatch[MapIndexed[Rule, x]]]]