1/BigInteger в C#

Question

1/BigInteger в C#

Я хочу сделать

BigInteger.ModPow(1/BigInteger, 2,5);

но 1/BigInteger всегда возвращайся 0, что приводит к тому, что результат 0 тоже. Я пытался искать некоторые BigDecimal класс для C#, но я ничего не нашел. Есть ли способ, как посчитать это, даже если нет BigDecimal?

2

c# biginteger inverse

Источник

user1158459 06 янв '13 в 11:06

3 ответа

Другие вопросы по тегам c# biginteger inverse

user445517 06 янв '13 в 11:55 2013-01-06 11:55 · Answer 1 · 2013-01-06 11:55

1/a 0 для |a|>1, так как BigIntegers используйте целочисленное деление, где дробная часть деления игнорируется. Я не уверен, какой результат вы ожидаете для этого.

Я предполагаю, что вы хотите, чтобы модульное мультипликативное обратное a по модулю mа не дробное число. Это обратное существует, если a а также m являются взаимно простыми, т.е. gcd(a, m) = 1,

На странице связанной википедии перечислены два стандартных алгоритма для вычисления модульного обратного мультипликатива:

Расширенный евклидов алгоритм, который работает для произвольных модулей
Это быстро, но имеет зависящее от входа время выполнения.
У меня нет кода C# под рукой, но портирование псевдокода из Википедии должно быть простым.
Используя теорему Эйлера:
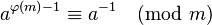
$i ^ {- 1} = i ^ {φ(n) -1}$
Это требует знания φ(m), т. Е. Вам нужно знать основные множители m. Это популярный выбор, когда m простое число и, следовательно, φ(m) = m-1, когда оно просто становится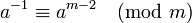 $a ^ {- 1} = a ^ {p-2}$ , Если вам нужно постоянное время выполнения, и вы знаете φ(м), это путь.
В C# это становится BigInteger.ModPow(a, phiOfM-1, m)

user1336654 06 янв '13 в 11:36 2013-01-06 11:36 · Answer 2 · 2013-01-06 11:36

Перегрузка / оператор, выбранный следующим образом:

public static BigInteger operator /(
        BigInteger dividend,
        BigInteger divisor
)

Смотрите BigInteger.Division Operator. Если результат между 0 а также 1 (что, вероятно, когда dividend является 1 как в вашем случае), потому что возвращаемое значение является целым числом, 0 возвращается, как видите.

Что вы пытаетесь сделать с ModPow метод? Вы понимаете, что 2,5 два аргумента, два и пять, а не "две точки пять"? Ваше намерение "взять квадрат по модулю 5"?

Если вы хотите деление с плавающей точкой, вы можете использовать:

1.0 / (double)yourBigInt

Обратите внимание на приведение к double, Это может потерять точность и даже "опуститься" до нуля, если yourBigInt слишком велик

user3627736 08 мар '15 в 21:26 2015-03-08 21:26 · Answer 3 · 2015-03-08 21:26

Например, вам нужно получить d в следующем:
3 * d = 1 (мод 9167368)

это в равной степени:
3 * d = 1 + k * 9167368, где k = 1, 2, 3, ...

переписать это:
d = (1 + k * 9167368)/ 3

Ваше d должно быть целым числом с самым низким k.
Напишем формулу:
д = (1 + к * фи)/ е

public static int MultiplicativeInverse(int e, int fi)
        {
            double result;
            int k = 1;
            while (true)
            {
                result = (1 + (k * fi)) / (double) e;
                if ((Math.Round(result, 5) % 1) == 0) //integer
                {
                    return (int)result;
                }
                else
                {
                    k++;
                }
            }
        }

давайте проверим этот код:

Assert.AreEqual(Helper.MultiplicativeInverse(3, 9167368), 6111579); // passed