Шаги для генерации дерева разбора из алгоритма CYK (обработка естественного языка)

Question

В настоящее время я работаю над проектом с участием НЛП. Я реализовал идентификатор CKY, указанный в Jurafsky and Martin (алгоритм на стр. 450). Созданная таблица фактически хранит нетерминалы в таблице (вместо обычных логических значений). Однако единственная проблема, которую я получаю, - это получить дерево разбора.

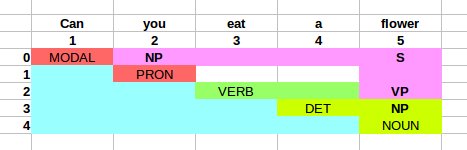
Вот иллюстрация того, что делает мой идентификатор CKY:

Это моя грамматика

          S -> NP VP 
          S -> VP 
          NP -> MODAL PRON | DET NP | NOUN VF | NOUN | DET NOUN | DET FILENAME
          MODAL -> 'MD'
          PRON -> 'PPSS' | 'PPO'
          VP -> VERB NP
          VP -> VERB VP
          VP -> ADVERB VP
          VP -> VF
          VERB -> 'VB' | 'VBN'
          NOUN -> 'NN' | 'NP'
          VF -> VERB FILENAME
          FILENAME -> 'NN' | 'NP'
          ADVERB -> 'RB'
          DET -> 'AT'

И это алгоритм:

for j  from i to LENGTH(words) do
    table[j-1,j] = A where A -> POS(word[j])
    for i from j-2 downto 0
        for k from i+1 to j-1
            table[i,j] = Union(table[i,j], A such that A->BC)
            where B is in table[i,k] and C is in table[k,j]

И вот как выглядит мой таблица разбора после заполнения:

Теперь, когда я знаю, что, поскольку S находится в [0,5], строка была проанализирована, и что для k = 1 (согласно алгоритму, приведенному в Martin и Jurafsky), мы имеем S -> table[0][2] таблица [2][5] т.е. S -> NP VP

Единственная проблема, которую я получаю, заключается в том, что я смог извлечь используемые правила, но тогда они в беспорядочном формате, то есть не на основе их появления в дереве разбора. Может кто-нибудь предложить алгоритм для поиска правильного дерева разбора?

Спасибо.

Answer 1

Вы должны рекурсивно посещать ячейки вашей таблицы и раскрывать их так же, как вы делали это для узла S, пока все не станет терминалом (так что вам больше нечего развернуть). В вашем примере вы сначала идете в ячейку [0] [2]; это терминал, вам не нужно ничего делать. Далее вы переходите к [2][5], это нетерминал, сделанный [2][3] и [3] [5]. Вы посещаете [2][3], это терминал. [3] [5] является нетерминалом, выполненным двумя терминалами. Вы сделали. Вот демо в Python:

class Node:
    '''Think this as a cell in your table'''
    def __init__(self, left, right, type, word):
        self.left = left
        self.right = right
        self.type = type
        self.word = word

# Declare terminals
t1 = Node(None,None,'MOD','can')
t2 = Node(None,None,'PRON','you')
t3 = Node(None,None,'VERB', 'eat')
t4 = Node(None,None,'DET', 'a')
t5 = Node(None,None,'NOUN','flower')

# Declare non-terminals
nt1 = Node(t1,t2, 'NP', None)
nt2 = Node(t4,t5, 'NP', None)
nt3 = Node(t3,nt2,'VP', None)
nt4 = Node(nt1,nt3,'S', None)

def unfold(node):
    # Check for a terminal
    if node.left == None and node.right == None:
        return node.word+"_"+node.type

    return "["+unfold(node.left)+" "+unfold(node.right)+"]_"+node.type

print unfold(nt4)

И вывод:

[[can_MOD you_PRON]_NP [eat_VERB [a_DET flower_NOUN]_NP]_VP]_S