Список функций Big-O для PHP

Question

После некоторого времени использования PHP я заметил, что не все PHP встроили функции так быстро, как ожидалось. Рассмотрим две ниже возможные реализации функции, которая определяет, является ли число простым, используя кэшированный массив простых чисел.

//very slow for large $prime_array
$prime_array = array( 2, 3, 5, 7, 11, 13, .... 104729, ... );
$result_array = array();
foreach( $prime_array => $number ) {
    $result_array[$number] = in_array( $number, $large_prime_array );
}

//speed is much less dependent on size of $prime_array, and runs much faster.
$prime_array => array( 2 => NULL, 3 => NULL, 5 => NULL, 7 => NULL,
                       11 => NULL, 13 => NULL, .... 104729 => NULL, ... );
foreach( $prime_array => $number ) {
    $result_array[$number] = array_key_exists( $number, $large_prime_array );
}

Это потому, что в in_array реализован линейный поиск O(n), который будет линейно замедляться как $prime_array растет. Где array_key_exists Функция реализована с использованием поиска хеша O(1), который не будет замедляться, если хеш-таблица не будет заполнена слишком сильно (в этом случае это только O(n)).

До сих пор мне приходилось открывать big-O методом проб и ошибок, а иногда и просматривать исходный код. Теперь к вопросу...

Был ли список теоретических (или практических) больших O раз для всех * встроенных функций PHP?

* или хотя бы интересные

Например, мне очень трудно предсказать, какой большой O функций перечислен, потому что возможная реализация зависит от неизвестных основных структур данных PHP: array_merge, array_merge_recursive, array_reverse, array_intersect, array_combine, str_replace (с входами в массив) и т. Д.

Answer 1

Поскольку кажется, что никто не делал этого раньше, я подумал, что было бы неплохо иметь его где-нибудь для справки. Я прошел через тест или тестирование кода, чтобы охарактеризовать array_* функции. Я пытался поставить более интересный Big-O в верхней части. Этот список не является полным.

Примечание. Все значения Big-O, рассчитанные в предположении хеш-поиска, равны O (1), хотя в действительности это O (n). Коэффициент n настолько низок, что накладные расходы на хранение достаточно большого массива могут повредить вам, прежде чем характеристики поиска Big-O начнут действовать. Например, разница между звонком array_key_exists при N=1 и N=1000000 - увеличение времени ~ 50%.

Интересные моменты:

1. isset/array_key_exists намного быстрее чем in_array а также array_search
2. +(союз) немного быстрее, чем array_merge (и выглядит лучше). Но это работает по-другому, так что имейте это в виду.
3. shuffle находится на том же уровне Big-O, что и array_rand
4. array_pop/array_push быстрее чем array_shift/array_unshift из-за повторного индексации штрафа

Поиски:

array_key_exists O (n), но действительно близко к O (1) - это из-за линейного опроса при столкновениях, но поскольку вероятность столкновений очень мала, коэффициент также очень мал. Я считаю, что вы рассматриваете поиск хешей как O (1), чтобы получить более реалистичный big-O. Например, разница между N=1000 и N=100000 замедляется только на 50%.

isset( $array[$index] ) O (n), но действительно близко к O (1) - он использует тот же поиск, что и array_key_exists. Поскольку это языковая конструкция, он будет кэшировать поиск, если ключ жестко закодирован, что ускоряет работу в тех случаях, когда один и тот же ключ используется повторно.

in_array O (n) - это потому, что он выполняет линейный поиск по массиву, пока не найдет значение.

array_search O (n) - он использует ту же основную функцию, что и in_array, но возвращает значение.

Функции очереди:

array_push O (∑ var_i, для всех я)

array_pop O (1)

array_shift O (n) - нужно переиндексировать все ключи

array_unshift O(n + ∑ var_i, для всех i) - необходимо переиндексировать все ключи

Пересечение массивов, объединение, вычитание:

array_intersect_key если пересечение 100% сделать O (Макс (param_i_size)*∑param_i_count, для всех i), если пересечение 0% пересечь O(∑param_i_size, для всех i)

array_intersect если пересечение 100% сделать O(n^2*∑param_i_count, для всех я), если пересечение 0% пересечь O(n^2)

array_intersect_assoc если пересечение 100% сделать O (Макс (param_i_size)*∑param_i_count, для всех i), если пересечение 0% пересечь O(∑param_i_size, для всех i)

array_diff O (π param_i_size, для всех i) - это произведение всех param_size

array_diff_key O (∑ param_i_size, для i!= 1) - это потому, что нам не нужно перебирать первый массив.

array_merge O (∑ array_i, i!= 1) - не нужно перебирать первый массив

+ (union) O(n), где n - это размер 2-го массива (т.е. array_first + array_second) - меньше накладных расходов, чем array_merge, так как не нужно перенумеровать

array_replace O (∑ array_i, для всех я)

Случайный:

shuffle На)

array_rand O (n) - Требуется линейный опрос.

Очевидный Big-O:

array_fill На)

array_fill_keys На)

range На)

array_splice O (смещение + длина)

array_slice O (смещение + длина) или O (n), если длина = NULL

array_keys На)

array_values На)

array_reverse На)

array_pad O (pad_size)

array_flip На)

array_sum На)

array_product На)

array_reduce На)

array_filter На)

array_map На)

array_chunk На)

array_combine На)

Я хотел бы поблагодарить Eureqa за то, что он упростил поиск Big-O функций. Это удивительная бесплатная программа, которая может найти наиболее подходящую функцию для произвольных данных.

РЕДАКТИРОВАТЬ:

Для тех, кто сомневается, что поиск в массиве PHP O(N)Я написал тест для проверки этого (они все еще эффективны O(1) для наиболее реалистичных значений).

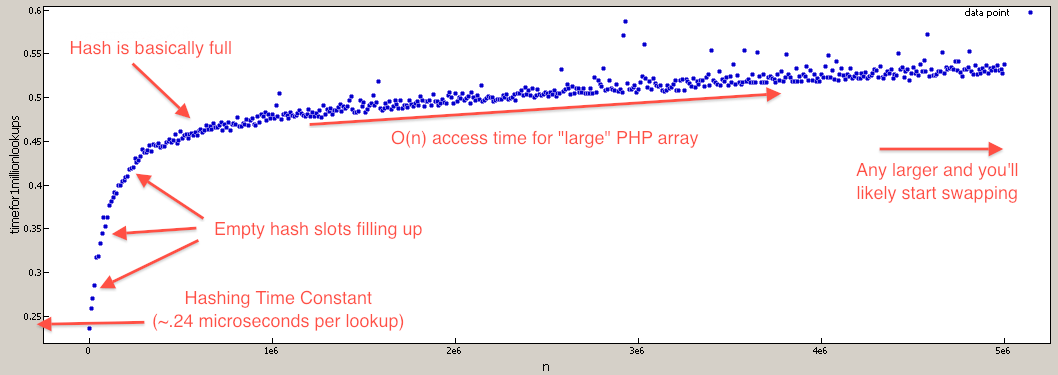
$tests = 1000000;
$max = 5000001;


for( $i = 1; $i <= $max; $i += 10000 ) {
    //create lookup array
    $array = array_fill( 0, $i, NULL );

    //build test indexes
    $test_indexes = array();
    for( $j = 0; $j < $tests; $j++ ) {
        $test_indexes[] = rand( 0, $i-1 );
    }

    //benchmark array lookups
    $start = microtime( TRUE );
    foreach( $test_indexes as $test_index ) {
        $value = $array[ $test_index ];
        unset( $value );
    }
    $stop = microtime( TRUE );
    unset( $array, $test_indexes, $test_index );

    printf( "%d,%1.15f\n", $i, $stop - $start ); //time per 1mil lookups
    unset( $stop, $start );
}

Answer 2

Объяснение кейса, который вы конкретно описываете, заключается в том, что ассоциативные массивы реализованы в виде хеш-таблиц, поэтому ищите по ключу (и, соответственно, array_key_exists) является O(1). Однако массивы не индексируются по значению, поэтому единственный способ в общем случае определить, существует ли значение в массиве, - это линейный поиск. Там нет ничего удивительного.

Я не думаю, что есть конкретная всесторонняя документация алгоритмической сложности методов PHP. Однако, если это достаточно большая задача, чтобы оправдать усилия, вы всегда можете просмотреть исходный код.

Answer 3

Вы почти всегда хотите использовать isset вместо array_key_exists, Я не смотрю на внутренности, но я уверен, что array_key_exists является O(N), потому что он перебирает каждый ключ массива, в то время как isset пытается получить доступ к элементу, используя тот же алгоритм хеширования, который используется при доступе к индексу массива. Это должно быть O(1).

Вот одна "ошибка", на которую стоит обратить внимание:

$search_array = array('first' => null, 'second' => 4);

// returns false
isset($search_array['first']);

// returns true
array_key_exists('first', $search_array);

---

Мне было любопытно, поэтому я оценил разницу:

<?php

$bigArray = range(1,100000);

$iterations = 1000000;
$start = microtime(true);
while ($iterations--)
{
    isset($bigArray[50000]);
}

echo 'is_set:', microtime(true) - $start, ' seconds', '<br>';

$iterations = 1000000;
$start = microtime(true);
while ($iterations--)
{
    array_key_exists(50000, $bigArray);
}

echo 'array_key_exists:', microtime(true) - $start, ' seconds';
?>

is_set: 0,132308959961 секунд
array_key_exists: 2,33202195168 секунд

Конечно, это не показывает сложность времени, но показывает, как эти две функции сравниваются друг с другом.

Чтобы проверить сложность времени, сравните количество времени, необходимое для запуска одной из этих функций на первом и последнем ключах.

Answer 4

Если бы у людей на практике возникали проблемы с ключевыми столкновениями, они реализовывали бы контейнеры со вторым поиском хеша или сбалансированным деревом. Сбалансированное дерево даст O(log n) в худшем случае и O(1) avg. case (сам хеш). В большинстве практических приложений с памятью эти издержки не стоят того, но, возможно, существуют базы данных, которые реализуют эту форму смешанной стратегии в качестве варианта по умолчанию.