Является ли угол между двумя углами

У меня 3 угла abc

а =315 б =20 с =45

Хорошо, так хотелось бы знать, давая все три, если б находится между а и с

у меня есть долгий способ сделать это сложение и вычитание, что, кажется, работает. Я просто хотел бы получить что-то меньшее и, возможно, более эффективное.

Спасибо

РЕДАКТИРОВАТЬ

Вот картинка, которую я пытаюсь сказать.

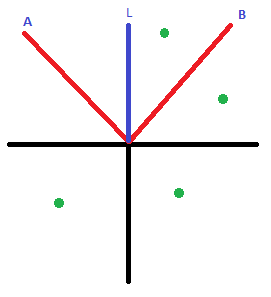
Хорошо, у меня есть угол L(в настоящее время 0), я добавляю 45(или любой угол) и вычитаю 45(или любой угол), чтобы получить a и b (мой угол обзора).

Теперь мне нужно знать, находится ли зеленая точка между a и b

(g> a ​​|| g > 0) && (g

так что на этой картинке будет только верхняя зеленая точка..

Извините, если я не проясняю себя, мой родной язык не английский

Источник

6 ответов

Решение

Проверьте:

(Если вы имеете в виду между, исключая границы)

(c - a) % 180 > 0 && b > a && b < c

(Если вы имеете в виду между, включая границу)

(c - a) % 180 >=0;b >= a && b <= c

(Этот ответ предполагает, что a,b,c >= 0; a,b,c < 360; a <= c)

Источник

У меня была похожая проблема. Я понял. Все расчеты в градусах. Мне нужно было рассчитать идентификатор местоположения GPS внутри прямоугольника.

Или мне нужно было увидеть, если угол x находится между углом check+r и угол check-r,

check-r<x<check+r,

Если тебе надо a<x<bнайти угол check во время a а также b а затем расстояние (r) из check от a или же b,

Метод нормализует, изменяет углы от -infinity... бесконечность до -180...180. Проверка метода, принимает аргументыx: угол, который нам нужен, чтобы увидеть, находится ли он между углами check-r и check + r.check: угол для проверки.r: проверка радиуса вокруг угла.

private static double normalize(double x) {
        x = x % 360;
        if (x>=180) {
            return x-360;
        }
        if (x<-180) {
            return x+360;
        }
        return x;
}
public static boolean check(double x, double check, double r) {
        x = x - check;
        x = normalize(x);
        return x<r && x>-r;
}
Источник

1-й выключен, каждый угол находится между двумя другими углами, что вы действительно спрашиваете:

Для заданных углов: a, b и g находится g вне угла отражения между a и b?

Вы можете просто пойти дальше и определить a как самый левый угол, а b как самый правый угол, или вы можете решить это, например, если любое из этих утверждений истинно, a - ваш самый левый угол:

  1. a ≤ b ∧ b - a ≤ π
  2. a> b ∧ a - b ≥ π

Для простоты предположим, что ваш самый левый угол равен l, а самый правый угол - r, и вы пытаетесь определить, находится ли g между ними.

Проблема здесь, кажется. По сути, мы ищем 3 положительных случая:

  1. l ≤ g ≤ r
  2. l ≤ g ∧ r
  3. g ≤ r ∧ r

Если вы просто определяете a как крайний левый и b как крайний правый, то все готово, и ваше состояние будет выглядеть так:

a <= g && g <= b ||
a <= g && b < a ||
g <= b && b < a

Однако, если вы вычислили l и r, вы заметите, что здесь есть возможность оптимизации при одновременном выполнении обоих процессов. Ваша функция будет выглядеть так:

if(a <= b) {
    if(b - a <= PI) {
        return a <= g && g <= b;
    } else {
        return b <= g || g <= a;
    }
} else {
    if(a - b <= PI) {
        return b <= g && g <= a;
    } else {
        return a <= g || g <= b;
    }
}

Или, если вам это нужно, вы можете перейти в это кошмарное состояние:

a <= b ?
(b - a <= PI && a <= g && g <= b) || (b - a > PI && (b <= g || g <= a)) :
(a - b <= PI && b <= g && g <= a) || (a - b > PI && (a <= g || g <= b))

Обратите внимание, что вся эта математика предполагает, что ваш ввод в радианах и в диапазоне [0: 2π].

Живой пример

Источник

Существует проблема с предлагаемыми решениями при обработке отрицательных углов (например, от =30 до =-29)

Предлагаемое (kotlin) исправление должно быть:

      fun isBetween(from:Float,to:Float,check:Float,inclusive:Boolean = true):Boolean{
   var a1 = to - from
   a1 = (a1 + 180f).mod(360f) - 180f
   if(a1<0f) a1+=360f

   var a2 = check - from
   a2 = (a2 + 180f).mod(360f) - 180f
   if(a2<0f) a2+=360f

   val between = if(inclusive)  a2<=a1 else a2<a1 && a2>0f
   println("$from->$to, $check, $between ($a1,$a2)")
   return between }
Источник

У меня лично недавно была такая же проблема, и я нашел контрпримеры для всех опубликованных ответов, поэтому я поделюсь своим собственным подходом.
Позволять a быть начальным углом и b конечный угол, и мы проверяем, c между ними по часовой стрелке, это означает, что когда вы идете из a в b ты должен пройти c, Подход проверки, является ли c находится в диапазоне от a в b дает вам ложные срабатывания, когда b больше, чем a численно. Например:a=80°, b=320° and c=150°: a <= c <= b что означало бы, что c находится между a а также b, Но это не так.
Подход, который работает, состоит в том, чтобы вычесть 360 из b если оно больше чем a а также вычесть 360 из c если c больше, чем a, Затем проверьте, a <= c <= b, В Java:

public static boolean isBetween(double c, double a, double b) {
    if (b > a) b -= 360;
    if (c > a) c -= 360;
    return a <= c && c <= b;
}

Это предполагает, что a, b и c находятся в диапазоне от 0 до 360.
Пример:

isBetween(150, 80, 320) => false
isBetween(30, 80, 320) => true
isBetween(340, 80, 320) => true
isBetween(140, 0, 160) => true
isBetween(180, 0, 160) => false
Источник

Если предположить, a > c, вы бы на самом деле использовали:

( b < a ) && ( b > c )

Это то же самое, что проверить, находится ли значение между нижней и верхней границами. Их угол не имеет значения, если только вы не хотите принять во внимание тот факт, что при движении по кругу угол 405 такой же, как угол 45, В этом случае вы можете просто использовать a % 360 чтобы получить угол между 0 а также 360,

Источник
Другие вопросы по тегам