График с использованием "С" и "График" с использованием блока (Mathematica)

Question

Я хочу описать проблему, с которой я столкнулся Plot с помощью With сохранить определенные параметры "локально". Я не обязательно прошу исправить: у меня проблема в понимании.

Иногда я использую конструкцию, такую ​​как следующее, чтобы получить участок:

Способ 1

plot1 = With[{vmax = 10, km = 10}, 
  Plot[Evaluate@((vmax x)/(km + x)), {x, 0, 100}, 
   AxesOrigin -> {0, 0}]]

Мне нравится этот метод, и он достаточно понятен даже пользователям, не являющимсяMathematica, что именно происходит.

Когда уравнения для построения становятся более сложными, мне нравится определять их вне графика (используя SetDelayed). Например:

f[x_] := (vmax x)/(km + x)

Однако следующее не работает

Способ 2

plot2 = With[{vmax = 10, km = 10}, 
  Plot[Evaluate@f[x], {x, 0, 100}, AxesOrigin -> {0, 0}]]

Я всегда наивно думал, что так и должно быть. Тем не менее, на основании справки, что

График обрабатывает переменную x как локальную, эффективно используя Block

Я использовал различные обходные пути, в основном что-то вроде следующего

Способ 3

plot3 = Plot[With[{vmax = 10, km = 10}, Evaluate@f[x]], {x, 0, 100}, 
  AxesOrigin -> {0, 0}]

Это кажется очень неловким, и обычно требует дальнейшего объяснения даже пользователям Mathematica.

Сюжетные выходы

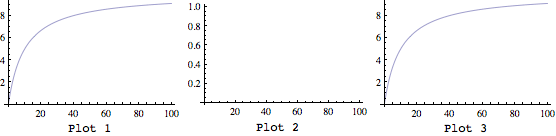
Однако недавно я случайно обнаружил, что замена Block за With в методе 2 работает точно так, как ожидалось.

Я могу, например, сделать что-то вроде следующего (что мне кажется очень универсальным подходом):

plot4 = Block[{vmax = {10, 10, 10}, km = { 10, 100, 1000}}, 
  Plot[Evaluate@f[x], {x, 0, 100}, AxesOrigin -> {0, 0}, 
   PlotStyle -> {Red, Green, Blue}]]

дающий

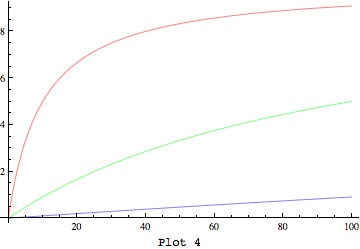
Мои вопросы следующие. Чем объясняется разница в поведении с With в методе 1 и 2? Должен ли я ожидать, что метод 2 не сработает? Кроме того, чем объясняется разница в поведении с Block а также With в методе 2? Должен ли я был в состоянии предсказать, что Block должно сработать?

Как ни странно, многие опытные решения были предложены мне более опытными, чем я, но никто не предложил использовать Block,

Наконец, мне нужно сохранить vmax а также km местный.(Они были определены алгебраически в другом месте)

Answer 1

Ваш вопрос не столько о Plot как это о том, как работают объемные конструкции. Основное замешательство здесь связано с различиями между лексическим и динамическим ограничением. И главный виновник это определение:

f[x_] := (vmax x)/(km + x)

Проблема в том, что это делает f неявно зависят от глобальных символов (переменных) vmax а также km, Я очень против такого рода конструкций, поскольку они приводят к бесконечной путанице. Теперь, что происходит, можно проиллюстрировать на следующем примере:

In[55]:= With[{vmax =1, km = 2},f[x]]

Out[55]= (vmax x)/(km+x)

Чтобы понять, почему это происходит, нужно понять, что означает лексическое определение. Мы знаем это With имеет HoldAll приписывать. Он работает так, что выглядит именно то, что находится внутри него, и заменяет переменные, найденные буквально в теле, их значениями из списка объявлений. Это происходит на этапе привязки переменных, и только тогда это позволяет телу оценить. Из этого ясно, что будет работать следующее:

In[56]:= With[{vmax =1, km = 2},Evaluate[f[x]]]

Out[56]= x/(2+x) 

Это сработало, потому что Evaluate переопределяет "часть" HoldAll атрибут With, заставляя тело оценивать прежде всего (привязка переменной и последующая оценка тела). Следовательно, было бы полностью эквивалентно использовать просто With[{vmax = 1, km = 2}, (vmax x)/(km + x)] выше, как вы можете видеть с Trace, Следующая часть головоломки почему

With[{vmax = 10, km = 10}, Plot[Evaluate@f[x], {x, 0, 100}, AxesOrigin -> {0, 0}]]

не работает. Это потому, что на этот раз мы не оцениваем тело в первую очередь. Наличие Evaluate влияет только f[x] внутри Plot, но не оценка Plot сама внутри With, Это иллюстрируется

In[59]:= With[{vmax = 10, km = 10}, q[Evaluate@f[x]]]

Out[59]= q[(vmax x)/(km + x)]

Более того, мы не хотим Plot оценить сначала, с тех пор значения vmax а также km не будет определен Однако все это With видит это f[x] и так как параметры vmax а также km там буквально не присутствуют (лексическое определение, помните), никакая замена не будет сделана. Должны ли мы использовать Block здесь и все будет работать, потому что Block использует динамическую область видимости, что означает, что он переопределяет значения во времени (часть стека выполнения, если хотите), а не на месте. Поэтому, используя Block[{a =1, b =2}, ff[x]] где ff неявно зависит от a а также b (примерно) эквивалентно a=1;b=2;ff[x] (с той разницей, что a а также b возобновить свои глобальные ценности после Block сфера оставлена). Так,

In[60]:= Block[{vmax = 10, km = 10}, q[Evaluate@f[x]]]

Out[60]= q[(10 x)/(10 + x)]

Чтобы сделать With версия работает, вам придется ввести выражение для f[x] (rhs), например так:

In[63]:= Unevaluated[With[{vmax = 10, km = 10}, q[f[x]]]] /. DownValues[f]

Out[63]= q[(10 x)/(10 + x)]

Обратите внимание, что это не сработает:

In[62]:= With[{fx = f[x]}, With[{vmax = 10, km = 10},  q[fx]]]

Out[62]= q[(vmax x)/(km + x)]

Но причина здесь довольно тонкая: в то время как внешняя With оценивает перед внутренним, обнаруживает конфликты имен переменных и переименовывает их. Правила гораздо более разрушительны, они не уважают внутренние ограничивающие конструкции.

РЕДАКТИРОВАТЬ

Если кто-то настаивает на вложенности With -с вот как можно обмануть механизм разрешения конфликтов имен With и заставить его работать:

In[69]:= With[{fx = f[x]}, With @@ Hold[{vmax = 10, km = 10}, q[fx]]]

Out[69]= q[(10 x)/(10 + x)]

С внешней With больше не может обнаружить присутствие внутреннего With (с помощью Apply[With,Hold[...]] делает внутреннее With эффективно динамически генерируется), он не делает никаких переименований, и тогда он работает. Это общий прием, чтобы обмануть лексический механизм разрешения имен, когда вы не хотите переименовывать, хотя необходимость его использования обычно указывает на плохой дизайн.

КОНЕЦ РЕДАКТИРОВАНИЯ

Но я отвлекся. Подводя итог, заставить ваш второй метод работать довольно сложно и требует действительно странных конструкций, таких как

Unevaluated[ With[{vmax = 10, km = 10}, Plot[Evaluate@f[x], {x, 0, 100},
     AxesOrigin -> {0, 0}]]] /.  DownValues[f]

или же

With[{fx = f[x]}, 
   With @@ Hold[{vmax = 10, km = 10}, 
       Plot[Evaluate@fx, {x, 0, 100}, AxesOrigin -> {0, 0}]]]

Еще раз: все это потому, что With должны явно видеть переменные в коде, чтобы сделать замены. По сравнению, Block в этом нет необходимости, он динамически заменяет значения в момент оценки на основе их измененных глобальных значений, как если бы вы делали присваивания, поэтому он работает.

Теперь настоящий виновник - это ваше определение f, Вы могли бы избежать всех этих неприятностей, если бы вы определили f с явной передачей параметров:

ff[x_, vmax_, km_] := (vmax x)/(km + x)

Теперь это работает из коробки:

With[{vmax = 10, km = 10}, 
   Plot[Evaluate@ff[x, vmax, km], {x, 0, 100}, AxesOrigin -> {0, 0}]]

потому что параметры явно присутствуют в сигнатуре вызова функции, и поэтому видны With,

Подводя итог: то, что вы наблюдали, является следствием взаимодействия лексической и динамической областей видимости. Лексические ограничивающие конструкции должны "видеть" свои переменные явно в коде на этапе привязки переменных (до оценки), иначе они не будут эффективными. Динамическая область видимости эффективно изменяет значения символов и в этом смысле менее требовательна (цена, которую вы платите, состоит в том, что код, использующий большое количество динамических областей, сложнее понять, поскольку он смешивает состояние и поведение). Основной причиной проблем является определение функции, которая создает неявные зависимости от глобальных символов (которых нет в списке формальных параметров функции). Лучше всего избегать таких конструкций. Все еще можно заставить вещи работать, но это значительно сложнее (как было показано выше), и, по крайней мере, для рассматриваемого случая, без веской причины.

Answer 2

Всего два комментария:

• используя блок, вам не нужно использовать Evaluate. То есть Блок [{vmax = 10, km = 2}, Plot[f[x], {x, 0, 100}] будет работать.

• Другой способ сделать это - определить правила замещения: rule = {vmax -> 10, km -> 10}; Участок [f[x] /. rule, {x, 0, 100}] Преимущество заключается в том, что вы можете повторно использовать правило в других выражениях.