Представление точек на круговом радиолокационном математическом подходе

Question

Я пишу простое приложение, которое может показать вам, что вокруг вас друзья, но не на карте нормалей, а на действительно круглом радаре, таком как UI:

( https://i.imgur.com/9Epw0Xh.png)

Вот так, где у меня каждый пользователь широта, долгота и, конечно же, мой собственный центр.

Я также измеряю расстояние каждого пользователя, чтобы расположить их так, чтобы данные, которые я знаю, были их широтой, долготой и расстоянием до меня.

По математическим причинам, скажем, радар имеет радиус 100 пикселей, я могу отдалить их на расстояние от меня, используя левое или правое позиционирование, но с точки зрения верха или низа это становится немного сложнее, так как я пытаюсь преобразовать их широту - мой широту в процентном результате, а затем поместить их на радар... но я думаю, что, может быть, есть и лучшие способы с полярными и декартовыми координатами, но я на самом деле немного невежественен.

Есть ли лучший подход с этими типами интерфейсов или что-то реализовано там?

Answer 1

1. преобразовать long,lat всех точек в декартово трехмерные пространственные координаты

   это преобразование сферическое -> декартово трехмерное пространство. Математика позади здесь. После этого все пункты (long,lat,alt) воля стала (x,y,z) где (0,0,0) центр Земли

   • X ось lat=0,long=0 [rad]
   • Y ось lat=0,long=+PI/2 [rad]
   • Z ось северная
   • XY самолет - экватор

   

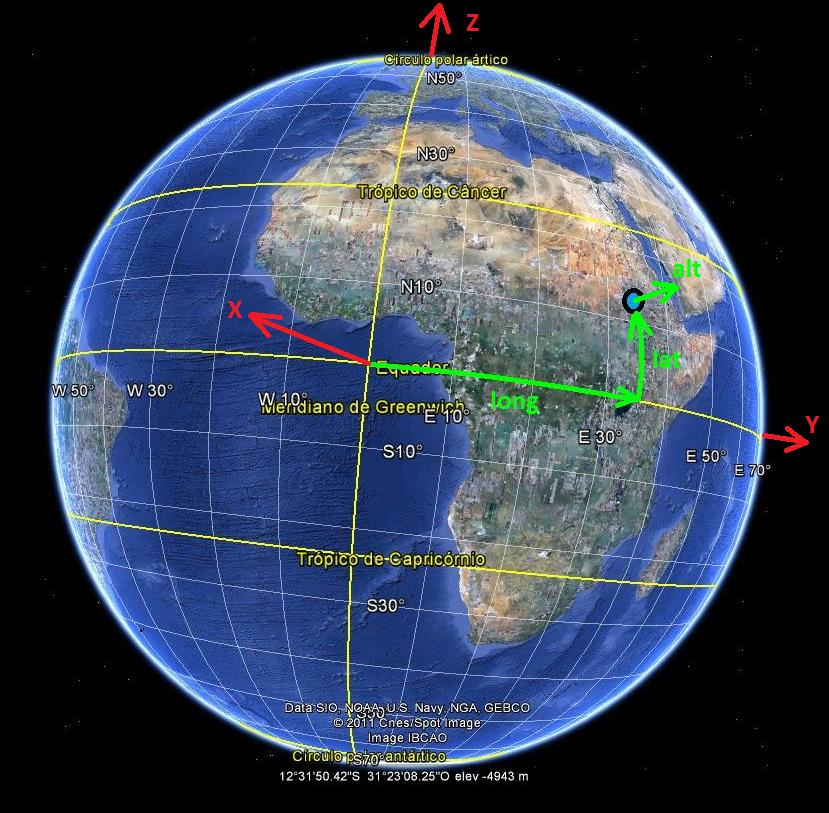
   Если вы хотите большей точности, используйте Землю как эллипсоид вместо сферы

   long = <     0 , +2*PI > [rad]
   lat  = < -PI/2 , +PI/2 > [rad]
   alt  = altitude above sea level [m]
   Re =6378141.4; [m]
   Rp =6356755.0; [m]
   
   R=alt+sqrt( (Re*cos(lat))^2 + (Rp*sin(lat))^2 )
   x=R*cos(lat)*cos(long)
   y=R*cos(lat)*sin(long)
   z=R*sin(lat)
   

2. создать локальную декартову систему координат RADAR

   

   В основном вам нужно получить 3D-векторы для X,Y,Z осях. Они должны быть перпендикулярны друг другу и направлены в правильном направлении от исходной точки RADAR. (P0),

   Вы можете использовать векторное умножение для этого, потому что оно создает перпендикулярный вектор к своим мультипликаторам. Направление зависит от порядка мультипликаторов, поэтому немного поэкспериментируйте.

   //altitude this one is easy
   Z = P0
   //north (chose one that is non zero, resp. bigger to avoid accuracy problems)
   X = (1,0,0) x Z // old X axis * Altitude
   X = (0,1,0) x Z // old Y axis * Altitude
   //east is now also easy
   Y = X x Z 
   // now normalize all of them to unit vectors
   X = X / |X|
   Y = Y / |Y|
   Z = Z / |Z|
   // and check if they are not negative (X,Y)
   // if they are then swap multiplicants or multiply by -1
   // do not forget that X is computed by two methods so swap the correct one
   

   • здесь математика позади построения матрицы преобразования 4x4
   • здесь вы можете увидеть на изображении разницу между однородными матрицами трехмерного преобразования 3x3 и матрицей прямого преобразования 3x3 и математикой

3. преобразовать все точки в систему координат RADAR

   просто умножьте все точки на матрицу преобразования RADAR M

   Q(i) = P(i)*M
   

   так что точки Q(i) теперь локально для RADAR

   • (0,0,0) означает радиолокационное происхождение (в центре)
   • (1,0,0) указывает на север
   • (0,1,0) указывает на восток
   • (0,0,1) указывает вверх

   так что теперь просто умножьте все кординаты на шкалу RADAR

   scale = RADAR_radius/RADAR_range;
   

   • RADAR_radius Размер вашего RADAR на экране в пикселях или единицах координат
   • RADAR_range максимальное расстояние, которое представляет самый большой круг RADAR [м]

   после этого просто нарисуйте точку в RADAR (поменять местами x,y потому что я использую X как север не Y), а также вы можете отбросить все точки, которые находятся дальше, чем на расстоянии. Также вы можете добавить 3D RADAR, как в старом Elite, добавив Z координата к вертикальной оси (или нарисовать линию L)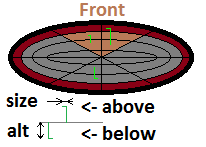

   

Надеюсь, это поможет немного и не слишком запутанно...