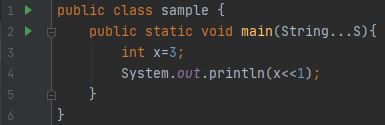
Что такое операторы побитового сдвига (bit-shift) и как они работают?
Я пытался изучать C в свободное время, и другие языки (C#, Java и т. Д.) Имеют ту же концепцию (и часто те же операторы) ...
Что мне интересно, так это то, что на уровне ядра происходит сдвиг битов (<<, >>, >>>), какие проблемы это может помочь решить, и что мешало скрыться за поворотом? Другими словами, абсолютное руководство для новичков по сдвигу во всей своей красе.
8 ответов
Операторы сдвига битов делают именно то, что подразумевает их имя. Они сдвигают биты. Вот краткое (или не очень краткое) введение в различные операторы сдвига.
Операторы
>>является арифметическим (или подписанным) оператором правого сдвига.>>>является логическим (или беззнаковым) правым оператором сдвига.<<является оператором левого сдвига и отвечает потребностям как логических, так и арифметических сдвигов.
Все эти операторы могут быть применены к целочисленным значениям (int, longвозможно short а также byte или же char). В некоторых языках применение операторов сдвига к любому типу данных меньше int автоматически изменяет размер операнда, чтобы быть int,
Обратите внимание, что <<< не является оператором, потому что это было бы излишним. Также обратите внимание, что C и C++ не различают операторы правого сдвига. Они обеспечивают только >> оператор, и поведение смещения вправо является реализацией, определенной для подписанных типов.
Сдвиг влево (<<)
Целые числа хранятся в памяти как последовательность битов. Например, номер 6 хранится как 32-разрядный int было бы:
00000000 00000000 00000000 00000110
Сдвиг этой битовой комбинации влево на одну позицию (6 << 1) приведет к числу 12:
00000000 00000000 00000000 00001100
Как видите, цифры смещены влево на одну позицию, а последняя цифра справа заполнена нулем. Вы также можете заметить, что смещение влево эквивалентно умножению на степени 2. Так 6 << 1 эквивалентно 6 * 2, а также 6 << 3 эквивалентно 6 * 8, Хороший оптимизирующий компилятор заменит умножения на сдвиги, когда это возможно.
Некруглое смещение
Обратите внимание, что это не круговые сдвиги. Сдвиг этого значения влево на одну позицию (3,758,096,384 << 1):
11100000 00000000 00000000 00000000
результаты в 3,221,225,472:
11000000 00000000 00000000 00000000
Цифра, которая сдвигается "с конца", теряется. Это не обернуть вокруг.
Логическое смещение вправо (>>>)
Логическое смещение вправо - это обратное смещение влево. Вместо того, чтобы перемещать биты влево, они просто перемещаются вправо. Например, смещение числа 12:
00000000 00000000 00000000 00001100
направо на одну позицию (12 >>> 1) вернемся к нашей оригинальной 6:
00000000 00000000 00000000 00000110
Итак, мы видим, что смещение вправо эквивалентно делению на степени 2.
Потерянные биты ушли
Однако сдвиг не может восстановить "потерянные" биты. Например, если мы сместим этот шаблон:
00111000 00000000 00000000 00000110
влево 4 позиции (939,524,102 << 4), мы получаем 2 147 483 744:
10000000 00000000 00000000 01100000
а потом возвращаемся ((939,524,102 << 4) >>> 4) мы получаем 134 217 734:
00001000 00000000 00000000 00000110
Мы не можем вернуть наше первоначальное значение, когда потеряли биты.
Арифметическое смещение вправо (>>)
Арифметическое смещение вправо точно такое же, как и логическое смещение вправо, за исключением того, что вместо заполнения нулями оно дополняется старшим значащим битом. Это связано с тем, что наиболее значимым битом является бит знака, или бит, который различает положительные и отрицательные числа. Заполняя старшим значащим битом, арифметическое смещение вправо сохраняет знак.
Например, если мы интерпретируем эту битовую комбинацию как отрицательное число:
10000000 00000000 00000000 01100000
у нас есть номер -2 147 483 552. Смещение этого положения вправо на 4 позиции с арифметическим сдвигом (-2 147 483 552 >> 4) даст нам:
11111000 00000000 00000000 00000110
или число -134,217,722.
Итак, мы видим, что мы сохранили знак наших отрицательных чисел, используя арифметическое смещение вправо, а не логическое смещение вправо. И еще раз, мы видим, что мы выполняем деление по степеням 2.
Допустим, у нас есть один байт:
0110110
Применение одного сдвига влево дает нам:
1101100
Крайний левый ноль был смещен из байта, и новый ноль был добавлен к правому концу байта.
Биты не переворачиваются; они отбрасываются. Это означает, что если вы измените его влево на 1101100, а затем на правое, вы не получите тот же результат.
Сдвиг влево на N эквивалентен умножению на 2 N.
Сдвиг вправо на N (если вы используете их дополнение) эквивалентен делению на 2 N и округлению до нуля.
Bitshifting можно использовать для безумно быстрого умножения и деления, если вы работаете со степенью 2. Почти все низкоуровневые графические подпрограммы используют сдвиг битов.
Например, еще в давние времена мы использовали режим 13h (320x200 256 цветов) для игр. В режиме 13h видеопамять распределялась последовательно на пиксель. Это означает, что для расчета местоположения для пикселя вы должны использовать следующую математику:
memoryOffset = (row * 320) + column
Теперь, в те дни и в возрасте, скорость была критической, поэтому мы использовали битовые сдвиги для выполнения этой операции.
Тем не менее, 320 не является степенью двойки, поэтому, чтобы обойти это, мы должны выяснить, что такое степень двойки, которая складывается вместе, составляет 320:
(row * 320) = (row * 256) + (row * 64)
Теперь мы можем преобразовать это в левые сдвиги:
(row * 320) = (row << 8) + (row << 6)
Для окончательного результата:
memoryOffset = ((row << 8) + (row << 6)) + column
Теперь мы получаем то же смещение, что и раньше, за исключением того, что вместо дорогостоящей операции умножения мы используем два битовых сдвига... в x86 это было бы примерно так (заметьте, это было всегда, так как я делал сборку (примечание редактора: исправлено пару ошибок и добавил 32-битный пример)):
mov ax, 320; 2 cycles
mul word [row]; 22 CPU Cycles
mov di,ax; 2 cycles
add di, [column]; 2 cycles
; di = [row]*320 + [column]
; 16-bit addressing mode limitations:
; [di] is a valid addressing mode, but [ax] isn't, otherwise we could skip the last mov
Итого: 28 циклов на любом древнем процессоре имели эти тайминги.
Vrs
mov ax, [row]; 2 cycles
mov di, ax; 2
shl ax, 6; 2
shl di, 8; 2
add di, ax; 2 (320 = 256+64)
add di, [column]; 2
; di = [row]*(256+64) + [column]
12 циклов на одном и том же древнем процессоре.
Да, мы бы усердно работали, чтобы сбить 16 тактов процессора.
В 32- или 64-битном режиме обе версии становятся намного короче и быстрее. Современные исполнительные процессоры вне порядка, такие как Intel Skylake (см. http://agner.org/optimize/), имеют очень быстрое аппаратное умножение (низкая задержка и высокая пропускная способность), поэтому выигрыш значительно меньше. Семейство AMD Bulldozer немного медленнее, особенно для 64-битного умножения. В процессорах Intel и AMD Ryzen две смены имеют немного меньшую задержку, но больше команд, чем умножение (что может привести к снижению пропускной способности):
imul edi, [row], 320 ; 3 cycle latency from [row] being ready
add edi, [column] ; 1 cycle latency (from [column] and edi being ready).
; edi = [row]*(256+64) + [column], in 4 cycles from [row] being ready.
против
mov edi, [row]
shl edi, 6 ; row*64. 1 cycle latency
lea edi, [edi + edi*4] ; row*(64 + 64*4). 1 cycle latency
add edi, [column] ; 1 cycle latency from edi and [column] both being ready
; edi = [row]*(256+64) + [column], in 3 cycles from [row] being ready.
Компиляторы сделают это за вас: посмотрите, как gcc, clang и MSVC все используют shift+lea при оптимизации return 320*row + col;,
Здесь самое интересное, что в x86 есть инструкция shift-and-add ( LEA ), которые могут делать небольшие сдвиги влево и добавлять в то же время, с производительностью, как и add инструкция. ARM еще более мощен: один операнд любой инструкции может быть смещен влево или вправо бесплатно. Таким образом, масштабирование с помощью постоянной времени компиляции, которая известна как степень 2, может быть даже более эффективным, чем умножение.
Хорошо, в наши дни... что-то более полезное сейчас - использовать битовую сдвиг для хранения двух 8-битных значений в 16-битном целом числе. Например, в C#:
// Byte1: 11110000
// Byte2: 00001111
Int16 value = ((byte)(Byte1 >> 8) | Byte2));
// value = 000011111110000;
В C++ компиляторы должны сделать это за вас, если вы использовали struct с двумя 8-битными членами, но на практике не всегда.
Битовые операции, включая сдвиг битов, являются основополагающими для низкоуровневого оборудования или встроенного программирования. Если вы прочитаете спецификацию для устройства или даже некоторые двоичные форматы файлов, вы увидите байты, слова и двойные слова, разбитые на битовые поля без выравнивания байтов, которые содержат различные интересующие значения. Доступ к этим битовым полям для чтения / записи является наиболее распространенным.
Простой реальный пример в графическом программировании - 16-битный пиксель представлен следующим образом:
bit | 15| 14| 13| 12| 11| 10| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Blue | Green | Red |
Чтобы получить значение зеленого, вы должны сделать это:
#define GREEN_MASK 0x7E0
#define GREEN_OFFSET 5
// Read green
uint16_t green = (pixel & GREEN_MASK) >> GREEN_OFFSET;
объяснение
Чтобы получить значение ТОЛЬКО зеленого цвета, которое начинается со смещения 5 и заканчивается на 10 (то есть длиной 6 бит), вам необходимо использовать (битовую) маску, которая при применении ко всему 16-битному пикселю даст только биты, которые нас интересуют.
#define GREEN_MASK 0x7E0
Соответствующей маской является 0x7E0, а в двоичном виде - 0000011111100000 (в 2016 году - десятичное число).
uint16_t green = (pixel & GREEN_MASK) ...;
Чтобы применить маску, вы используете оператор AND (&).
uint16_t green = (pixel & GREEN_MASK) >> GREEN_OFFSET;
После применения маски вы получите 16-битное число, которое на самом деле является просто 11-битным числом, поскольку его MSB находится в 11-м бите. Зеленый имеет длину всего 6 бит, поэтому нам нужно уменьшить его, используя сдвиг вправо (11 - 6 = 5), следовательно, использование 5 в качестве смещения (#define GREEN_OFFSET 5).
Также распространено использование битовых сдвигов для быстрого умножения и деления на степени 2:
i <<= x; // i *= 2^x;
i >>= y; // i /= 2^y;
Битовая маскировка и сдвиг
Сдвиг битов часто используется в низкоуровневых графических программах. Например, заданное значение цвета пикселя закодировано в 32-битном слове.
Pixel-Color Value in Hex: B9B9B900
Pixel-Color Value in Binary: 10111001 10111001 10111001 00000000
Для лучшего понимания одно и то же двоичное значение, помеченное с какими разделами, представляет часть какого цвета.
Red Green Blue Alpha
Pixel-Color Value in Binary: 10111001 10111001 10111001 00000000
Допустим, например, что мы хотим получить значение зеленого цвета этого пикселя. Мы можем легко получить это значение, маскируя и сдвигая.
Наша маска:
Red Green Blue Alpha
color : 10111001 10111001 10111001 00000000
green_mask : 00000000 11111111 00000000 00000000
masked_color = color & green_mask
masked_color: 00000000 10111001 00000000 00000000
Логичный & Оператор обеспечивает сохранение только тех значений, для которых маска равна 1. Последнее, что нам теперь нужно сделать, - это получить правильное целочисленное значение, сдвинув все эти биты вправо на 16 позиций (логическое смещение вправо).
green_value = masked_color >>> 16
Et voilá, у нас есть целое число, представляющее количество зеленого цвета в пикселях:
Pixels-Green Value in Hex: 000000B9
Pixels-Green Value in Binary: 00000000 00000000 00000000 10111001
Pixels-Green Value in Decimal: 185
Это часто используется для кодирования или декодирования форматов изображений, таких как jpg,png,...,
Одна проблема заключается в том, что следующее зависит от реализации (в соответствии со стандартом ANSI):
char x = -1;
x >> 1;
х теперь может быть 127 (01111111) или еще -1 (11111111).
На практике это обычно последнее.
Я пишу только советы и рекомендации, может оказаться полезным в тестах / экзаменах.
n = n*2:n = n<<1n = n/2:n = n>>1- Проверка, является ли n степенью 2 (1,2,4,8,...): проверьте
!(n & (n-1)) - Получение х-го бита
n:n |= (1 << x) - Проверка, является ли х четным или нечетным:
x&1 == 0(четное) - Переключите n-й бит x:
x ^ (1<<n)
Обратите внимание, что в реализации Java количество бит для сдвига изменяется в зависимости от размера источника.
Например:
(long) 4 >> 65
равно 2. Можно ожидать, что смещение битов вправо 65 раз приведет к обнулению всего, но на самом деле это эквивалентно:
(long) 4 >> (65 % 64)
Это верно для <<, >> и >>>. Я не пробовал это на других языках.
Побитовые операторы используются для выполнения операций на битовом уровне или для различных способов манипулирования битами. Побитовые операции оказываются намного быстрее и иногда используются для повышения эффективности программы. В основном побитовые операторы могут применяться к целочисленным типам: long, int, short, char и byte.
Операторы побитового сдвига
Они делятся на две категории, сдвиг влево и сдвиг вправо.
- Left Shift (<<): оператор сдвига влево сдвигает все биты значения влево указанное количество раз. Синтаксис: значение << число. Здесь num указывает номер позиции, на которую нужно сдвинуть значение влево. То есть << перемещает все биты в указанном значении влево на количество битовых позиций, заданное параметром num. Для каждого сдвига влево старший бит сдвигается (и игнорируется / теряется), а справа вводится ноль. Это означает, что когда к 32-битному компилятору применяется сдвиг влево, биты теряются, как только они смещаются за разрядную позицию 31. Если компилятор 64-битный, то биты теряются после битовой позиции 63.
Вывод: 6. Здесь двоичное представление 3 равно 0...0011(учитывая 32-битную систему), поэтому при однократном сдвиге ведущий ноль игнорируется / теряется, а все остальные 31 бит сдвигаются влево. И в конце добавляется ноль. Таким образом, получилось 0...0110, десятичное представление этого числа - 6.
- В случае отрицательного числа:
Выход: -2, в java отрицательное число представлено двумя дополнениями. SO, -1 представляет собой 2^32-1, что эквивалентно 1....11(учитывая 32-битную систему). При однократном сдвиге ведущий бит игнорируется / теряется, а остальные 31 бит сдвигаются влево, а к последнему добавляется ноль. Таким образом, получается 11...10, а его десятичный эквивалент -2. Итак, я думаю, вы знаете достаточно о левой смене и о том, как она работает.
- Сдвиг вправо (>>): оператор сдвига вправо сдвигает все биты значения вправо заданный раз. Синтаксис: value >> num, num определяет количество позиций для сдвига значения вправо в value. То есть >> перемещает / сдвигает все биты в указанном значении вправо на количество битовых позиций, заданное параметром num. Следующий фрагмент кода сдвигает значение 35 вправо на две позиции:
Вывод: 8, поскольку двоичное представление числа 35 в 32-битной системе равно 00...00100011, поэтому, когда мы сдвигаем его вправо два раза, первые 30 ведущих битов перемещаются / сдвигаются вправо, а два младших разряда биты теряются / игнорируются, и к старшим битам добавляются два нуля. Таким образом, он становится 00....00001000, десятичный эквивалент этого двоичного представления равен 8. Или есть простой математический трюк, чтобы узнать результат следующего кода: Чтобы обобщить это, мы можем сказать, что x >> y = этаж (x/pow(2,y)). Рассмотрим приведенный выше пример, x=35 и y=2, поэтому 35/2^2 = 8,75, и если мы возьмем минимальное значение, то ответ будет 8.
Выход:
Но помните, что этот трюк подходит для малых значений y, если вы берете большие значения y, это дает неправильный результат.
- В случае отрицательного числа: из-за отрицательных чисел оператор сдвига вправо работает в двух режимах со знаком и без знака. В операторе сдвига вправо со знаком (>>), в случае положительного числа, он заполняет начальные биты нулем, а в случае отрицательного числа он заполняет начальные биты цифрой 1. Для сохранения знака. Это называется "расширением знака".
Вывод: -5. Как я объяснил выше, компилятор сохраняет отрицательное значение как дополнение до 2. Таким образом, -10 представляется как 2^32-10 и в двоичном представлении с учетом 32-битной системы 11....0110. Когда мы сдвигаем / перемещаем один раз, первый 31 ведущий бит сдвигается в правую сторону, а младший бит теряется / игнорируется. Таким образом, оно становится 11...0011, а десятичное представление этого числа - -5 (как узнать знак числа? Потому что ведущий бит равен 1). Интересно отметить, что если вы сдвинете -1 вправо, результат всегда останется -1, поскольку расширение знака приводит к увеличению количества единиц в старших битах.
- Беззнаковый сдвиг вправо (>>>): этот оператор также сдвигает биты вправо. Разница между знаком и без знака заключается в том, что последний заполняет ведущие биты 1, если число отрицательное, а первый заполняет ноль в любом случае. Теперь возникает вопрос, зачем нам нужна операция вправо без знака, если мы получаем желаемый результат с помощью оператора сдвига вправо со знаком. Поймите это на примере. Если вы перемещаете что-то, что не представляет собой числовое значение, вы можете не захотеть, чтобы расширение знака имело место. Это обычная ситуация, когда вы работаете с пиксельными значениями и графикой. В этих случаях вы, как правило, захотите сдвинуть ноль в старший бит независимо от того, каким было его начальное значение.
Вывод: 2147483647, потому что -2 в 32-битной системе представлено как 11...10. Когда мы сдвигаем бит на единицу, первый 31 ведущий бит перемещается / сдвигается вправо, а младший бит теряется / игнорируется, а к ведущему биту добавляется ноль. Таким образом, он становится 011...1111 (2^31-1), а его десятичный эквивалент - 2147483647.
Некоторые полезные битовые операции / манипуляции в Python. Реализовал ответы @Ravi Prakash в python.
# basic bit operations
# int to bin
print(bin(10))
# bin to int
print(int('1010',2))
# multiplying x with 2 .... x**2== x << 1
print(200<<1)
# dividing x with 2 .... x /2 == x >> 1
print(200>>1)
# modulo x with 2 .... x%2 == x&1
if 20&1==0:
print("20 is a even number")
# check if n is power of 2 : check !(n & (n-1))
print(not(33 &(33-1)))
# getting xth bit of n : (n>>x)&1
print((10>>2)&1) # bin of 10==1010 and 2nd bit is 0
# toggle nth bit of x : x^(1<<n)
# take bin(10)==1010 and toggling 2nd bit in bin(10) we get 1110 === bin(14)
print(10^(1<<2))
Операторы побитового сдвига перемещают битовые значения двоичного объекта. Левый операнд указывает значение, которое нужно сдвинуть. Правый операнд определяет количество позиций, на которые должны быть сдвинуты биты в значении. Результат не является lvalue. Оба операнда имеют одинаковый приоритет и ассоциативны слева направо.
Operator Usage
<< Indicates the bits are to be shifted to the left.
>> Indicates the bits are to be shifted to the right.
Каждый операнд должен иметь целочисленный или перечисляемый тип. Компилятор выполняет интегральное продвижение операндов, а затем правый операнд преобразуется в тип int. Результат имеет тот же тип, что и левый операнд (после арифметических преобразований).
Правый операнд не должен иметь отрицательного значения или значения, которое больше или равно ширине в битах сдвигаемого выражения. Результат побитового сдвига таких значений непредсказуем.
Если правый операнд имеет значение 0, результатом является значение левого операнда (после обычных арифметических преобразований).
Оператор << заполняет освободившиеся биты нулями. Например, если left_op имеет значение 4019, битовый шаблон (в 16-битном формате) left_op будет следующим:
0000111110110011
Выражение left_op << 3 дает:
0111110110011000
Выражение left_op >> 3 дает:
0000000111110110
Помните, что на платформе Windows доступна только 32-битная версия PHP.
Тогда, если вы, например, сдвинете << или >> более чем на 31 бит, результаты будут неожиданными. Обычно вместо нуля возвращается оригинальное число, и это может быть очень сложной ошибкой.
Конечно, если вы используете 64-битную версию PHP (unix), вам следует избегать сдвига более чем на 63 бита. Однако, например, MySQL использует 64-битный BIGINT, поэтому не должно быть никаких проблем с совместимостью.
ОБНОВЛЕНИЕ: В PHP7 Windows сборки php наконец-то могут использовать полные 64-битные целые числа: размер целого зависит от платформы, хотя обычно используется максимальное значение около двух миллиардов (это 32- битные знаки ). Максимальное значение для 64-разрядных платформ обычно составляет около 9E18, за исключением Windows до PHP 7, где оно всегда было 32-разрядным.