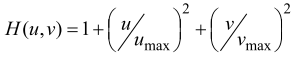Применить параболический фильтр в частотной области

Question

Как это повлияет на исходное изображение применения этого фильтра:

в частотной области?

Как определить эффект без использования компьютера (на бумаге)?

Этот фильтр (H) уже находится в частотной области.

Answer 1

Вы можете попытаться увидеть, что вы получите для разных значений.

Первое, что вы можете заметить, это то, что в функции фильтра есть 1, фильтр только усиливает и не пробуждает частоту.

Во-вторых, если мы посмотрим на два других термина: мы усиливаем каждую пространственную частоту как функцию максимальной частоты в каждом направлении. Поэтому для малых частот усиление будет минимальным, потому что (smallFreq/largeFreq) < 1 и возведение в квадрат этого слагаемого только сделает это значение еще меньшим.

Для больших частот усиление будет больше. Для uMax и vMax усиление может быть в 3 раза больше исходного значения.

Если вы хотите знать, как повлияет исходное изображение, не возвращаясь к пространственной области, вы можете сказать, что области с высокими частотами (края на изображении) будут иметь очень высокое значение, а области с низкими частотами (области с более или менее постоянное значение) останется прежним.

В заключение, похоже, ваш фильтр является фильтром повышения резкости.

Answer 2

Я предполагаю, u_max а также v_max являются постоянными параметрами, и что без использования компьютера вы имеете в виду не просто рассчитать эффект численно, а скорее предпочесть аналитическое решение.

Фильтрация / умножение в пространстве Фурье соответствует свертке в реальном пространстве с функцией фильтра, преобразованной Фурье. Чтобы узнать ядро ​​свертки, то есть определить эффект, необходимо выполнить обратное преобразование Фурье данного фильтра. H должен быть построен, если он существует.

Mathematica решает

InverseFourierTransform[1+(u/umax)^2+(v/vmax)^2,{u,v},{x,y}]

в

2 \[Pi] DiracDelta[x] DiracDelta[y]-(2 \[Pi] DiracDelta[y] (DiracDelta^\[Prime]\[Prime])[x])/umax^2-(2 \[Pi] DiracDelta[x] (DiracDelta^\[Prime]\[Prime])[y])/vmax^2

то есть к запутанному выражению дельта-функций Дирака от x и y, а также от вторых производных дельта-функций Дирака.

Мне слишком сложно представить точную форму этого. Одна из проблем заключается в том, что интеграл вашего фильтра H не ограничен, поэтому мы все равно получаем проблему с нормализацией (или с существованием преобразования Фурье), но (используя компьютер) для визуализации результатов я обнаружил, что ядро ​​свертки равно нулю для либо x, либо y не равно нулю и является максимальным при x=y=0 и резко падает по оси x и y и является симметричным относительно осей x и y.

Итак, в заключение, это очень странный фильтр, который немного сглаживает вдоль осей. Я бы тоже ожидал резкости, как это делает Амитей в своем ответе, так что это немного удивительно.