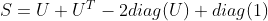R: преобразовать верхнюю треугольную часть матрицы в симметричную матрицу

Question

У меня есть верхняя треугольная часть матрицы в R (без диагонали) и я хочу сгенерировать симметричную матрицу из верхней треугольной части (с 1 по диагонали, но это можно отрегулировать позже). Я обычно делаю это так:

res.upper <- rnorm(4950)
res <- matrix(0, 100, 100)
res[upper.tri(res)] <- res.upper
rm(res.upper)
diag(res) <- 1
res[lower.tri(res)]  <- t(res)[lower.tri(res)]

Это прекрасно работает, но теперь я хочу работать с очень большими матрицами. Таким образом, я бы хотел избежать необходимости сохранять res.upper и res (заполненные 0) одновременно. Есть ли способ, которым я могу напрямую преобразовать res.upper в симметричную матрицу без предварительной инициализации матрицы res?

Answer 1

Я думаю, что здесь есть две проблемы.

теперь я хочу работать с очень большими матрицами

Тогда не используйте код R, чтобы сделать эту работу. R будет использовать гораздо больше памяти, чем вы ожидаете. Попробуйте следующий код:

res.upper <- rnorm(4950)
res <- matrix(0, 100, 100)
tracemem(res)  ## trace memory copies of `res`
res[upper.tri(res)] <- res.upper
rm(res.upper)
diag(res) <- 1
res[lower.tri(res)]  <- t(res)[lower.tri(res)]

Вот что вы получите:

> res.upper <- rnorm(4950)  ## allocation of length 4950 vector
> res <- matrix(0, 100, 100)  ## allocation of 100 * 100 matrix
> tracemem(res)
[1] "<0xc9e6c10>"
> res[upper.tri(res)] <- res.upper
tracemem[0xc9e6c10 -> 0xdb7bcf8]: ## allocation of 100 * 100 matrix
> rm(res.upper)
> diag(res) <- 1
tracemem[0xdb7bcf8 -> 0xdace438]: diag<-  ## allocation of 100 * 100 matrix
> res[lower.tri(res)]  <- t(res)[lower.tri(res)]
tracemem[0xdace438 -> 0xdb261d0]: ## allocation of 100 * 100 matrix
tracemem[0xdb261d0 -> 0xccc34d0]: ## allocation of 100 * 100 matrix

В R вы должны использовать 5 * (100 * 100) + 4950 двойные слова, чтобы закончить эти операции. В то время как в C, вам нужно только самое большее 4950 + 100 * 100 двойные слова (На самом деле, 100 * 100это все что нужно! Об этом позже расскажу). Трудно переписать объект непосредственно в R без дополнительного выделения памяти.

Есть ли способ, которым я могу напрямую конвертировать res.upper в симметричную матрицу без инициализации матрицы res первый?

Вы должны выделить память для res потому что это то, что вы в конечном итоге; но нет необходимости выделять память для res.upper, Вы можете инициализировать верхний треугольник, одновременно заполняя нижний треугольник. Рассмотрим следующий шаблон:

#include <Rmath.h>  // use: double rnorm(double a, double b)
#include <R.h>  // use: getRNGstate() and putRNGstate() for randomness
#include <Rinternals.h>  // SEXP data type

## N is matrix dimension, a length-1 integer vector in R
## this function returns the matrix you want
SEXP foo(SEXP N) {
  int i, j, n = asInteger(N);
  SEXP R_res = PROTECT(allocVector(REALSXP, n * n));  // allocate memory for `R_res`
  double *res = REAL(R_res);
  double tmp;  // a local variable for register reuse
  getRNGstate();
  for (i = 0; i < n; i++) {
    res[i * n + i] = 1.0;  // diagonal is 1, as you want
    for (j = i + 1; j < n; j++) {
      tmp = rnorm(0, 1);  
      res[j * n + i] = tmp; // initialize upper triangular
      res[i * n + j] = tmp;  // fill lower triangular
      }
    }
  putRNGstate();
  UNPROTECT(1);
  return R_res;
  }

Код не был оптимизирован, так как используется целочисленное умножение j * n + i для адресации в самом внутреннем цикле приведет к снижению производительности. Но я верю, что вы можете переместить умножение за пределы внутреннего цикла и оставить только сложение внутри.

Answer 2

Чтобы получить симметричную матрицу из верхней или нижней треугольной матрицы, вы можете добавить матрицу к ее транспонированию и вычесть диагональные элементы. Уравнение связано ниже.

diag(U) — диагональная матрица с диагональными элементами матрицы U.

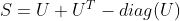
      ultosymmetric=function(m){
  m = m + t(m) - diag(diag(m))
return (m)}

Если вы хотите, чтобы диагональные элементы были равны 1, вы можете сделать это.

      ultosymmetric_diagonalone=function(m){
  m = m + t(m) - 2*diag(diag(m)) + diag(1,nrow=dim(m)[1])
return (m)}