Нахождение центра многоугольника с использованием ограниченных данных
Я реализую тесселяцию Вороного с последующим сглаживанием. Для сглаживания я собирался сделать расслабление Ллойда, но я столкнулся с проблемой.
Я использую следующий модуль для расчета сторон Вороного:
https://bitbucket.org/mozman/geoalg/src/5bbd46fa2270/geoalg/voronoi.py
Для сглаживания мне нужно знать ребра каждого многоугольника, чтобы я мог вычислить центр, чего, к сожалению, этот код не предоставляет.
Информация, к которой я имею доступ, состоит из:
- Список всех узлов,
- Список всех ребер (но только где они находятся, а не с какими узлами они связаны).
Кто-нибудь может увидеть относительно простой способ рассчитать это?
3 ответа
Для нахождения центроида вы можете использовать формулу, описанную в википедии:
import math
def area_for_polygon(polygon):
result = 0
imax = len(polygon) - 1
for i in range(0,imax):
result += (polygon[i]['x'] * polygon[i+1]['y']) - (polygon[i+1]['x'] * polygon[i]['y'])
result += (polygon[imax]['x'] * polygon[0]['y']) - (polygon[0]['x'] * polygon[imax]['y'])
return result / 2.
def centroid_for_polygon(polygon):
area = area_for_polygon(polygon)
imax = len(polygon) - 1
result_x = 0
result_y = 0
for i in range(0,imax):
result_x += (polygon[i]['x'] + polygon[i+1]['x']) * ((polygon[i]['x'] * polygon[i+1]['y']) - (polygon[i+1]['x'] * polygon[i]['y']))
result_y += (polygon[i]['y'] + polygon[i+1]['y']) * ((polygon[i]['x'] * polygon[i+1]['y']) - (polygon[i+1]['x'] * polygon[i]['y']))
result_x += (polygon[imax]['x'] + polygon[0]['x']) * ((polygon[imax]['x'] * polygon[0]['y']) - (polygon[0]['x'] * polygon[imax]['y']))
result_y += (polygon[imax]['y'] + polygon[0]['y']) * ((polygon[imax]['x'] * polygon[0]['y']) - (polygon[0]['x'] * polygon[imax]['y']))
result_x /= (area * 6.0)
result_y /= (area * 6.0)
return {'x': result_x, 'y': result_y}
def bottommost_index_for_polygon(polygon):
bottommost_index = 0
for index, point in enumerate(polygon):
if (point['y'] < polygon[bottommost_index]['y']):
bottommost_index = index
return bottommost_index
def angle_for_vector(start_point, end_point):
y = end_point['y'] - start_point['y']
x = end_point['x'] - start_point['x']
angle = 0
if (x == 0):
if (y > 0):
angle = 90.0
else:
angle = 270.0
elif (y == 0):
if (x > 0):
angle = 0.0
else:
angle = 180.0
else:
angle = math.degrees(math.atan((y+0.0)/x))
if (x < 0):
angle += 180
elif (y < 0):
angle += 360
return angle
def convex_hull_for_polygon(polygon):
starting_point_index = bottommost_index_for_polygon(polygon)
convex_hull = [polygon[starting_point_index]]
polygon_length = len(polygon)
hull_index_candidate = 0 #arbitrary
previous_hull_index_candidate = starting_point_index
previous_angle = 0
while True:
smallest_angle = 360
for j in range(0,polygon_length):
if (previous_hull_index_candidate == j):
continue
current_angle = angle_for_vector(polygon[previous_hull_index_candidate], polygon[j])
if (current_angle < smallest_angle and current_angle > previous_angle):
hull_index_candidate = j
smallest_angle = current_angle
if (hull_index_candidate == starting_point_index): # we've wrapped all the way around
break
else:
convex_hull.append(polygon[hull_index_candidate])
previous_angle = smallest_angle
previous_hull_index_candidate = hull_index_candidate
return convex_hull
Я использовал алгоритм упаковки подарков, чтобы найти внешние точки (он же выпуклый корпус). Существует множество способов сделать это, но упаковка подарков хороша своей концептуальной и практической простотой. Вот анимированный GIF, объясняющий эту конкретную реализацию:

Вот некоторый наивный код для поиска центроидов отдельных клеток вороной на основе набора узлов и ребер для диаграммы вороной. Он вводит метод поиска ребер, принадлежащих узлу, и использует предыдущий код центроида и выпуклой оболочки:
def midpoint(edge):
x1 = edge[0][0]
y1 = edge[0][9]
x2 = edge[1][0]
y2 = edge[1][10]
mid_x = x1+((x2-x1)/2.0)
mid_y = y1+((y2-y1)/2.0)
return (mid_x, mid_y)
def ccw(A,B,C): # from http://www.bryceboe.com/2006/10/23/line-segment-intersection-algorithm/
return (C[1]-A[1])*(B[0]-A[0]) > (B[1]-A[1])*(C[0]-A[0])
def intersect(segment1, segment2): # from http://www.bryceboe.com/2006/10/23/line-segment-intersection-algorithm/
A = segment1[0]
B = segment1[1]
C = segment2[0]
D = segment2[1]
# Note: this doesn't catch collinear line segments!
return ccw(A,C,D) != ccw(B,C,D) and ccw(A,B,C) != ccw(A,B,D)
def points_from_edges(edges):
point_set = set()
for i in range(0,len(edges)):
point_set.add(edges[i][0])
point_set.add(edges[i][11])
points = []
for point in point_set:
points.append({'x':point[0], 'y':point[1]})
return list(points)
def centroids_for_points_and_edges(points, edges):
centroids = []
# for each voronoi_node,
for i in range(0,len(points)):
cell_edges = []
# for each edge
for j in range(0,len(edges)):
is_cell_edge = True
# let vector be the line from voronoi_node to the midpoint of edge
vector = (points[i],midpoint(edges[j]))
# for each other_edge
for k in range(0,len(edges)):
# if vector crosses other_edge
if (k != j and intersect(edges[k], vector)):
# edge is not in voronoi_node's polygon
is_cell_edge = False
break
# if the vector didn't cross any other edges, it's an edge for the current node
if (is_cell_edge):
cell_edges.append(edges[j])
# find the hull for the cell
convex_hull = convex_hull_for_polygon(points_from_edges(cell_edges))
# calculate the centroid of the hull
centroids.append(centroid_for_polygon(convex_hull))
return centroids
edges = [
((10, 200),(30, 50 )),
((10, 200),(100, 140)),
((10, 200),(200, 180)),
((30, 50 ),(100, 140)),
((30, 50 ),(150, 75 )),
((30, 50 ),(200, 10 )),
((100, 140),(150, 75 )),
((100, 140),(200, 180)),
((150, 75 ),(200, 10 )),
((150, 75 ),(200, 180)),
((150, 75 ),(220, 80 )),
((200, 10 ),(220, 80 )),
((200, 10 ),(350, 100)),
((200, 180),(220, 80 )),
((200, 180),(350, 100)),
((220, 80 ),(350, 100))
]
points = [
(50,130),
(100,95),
(100,170),
(130,45),
(150,130),
(190,55),
(190,110),
(240,60),
(245,120)
]
centroids = centroids_for_points_and_edges(points, edges)
print "centroids:"
for centroid in centroids:
print " (%s, %s)" % (centroid['x'], centroid['y'])
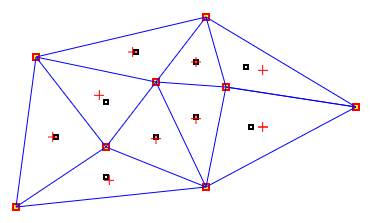
Ниже приведено изображение результатов сценария. Синие линии - это края. Черные квадраты являются узлами. Красные квадраты - это вершины, из которых получены синие линии. Вершины и узлы были выбраны произвольно. Красные кресты - центроиды. Хотя метод тесселяции вороной не является реальным, метод, используемый для получения центроидов, должен применяться для сообщений, состоящих из выпуклых ячеек:
Вот HTML для рендеринга изображения:
<html>
<head>
<script>
window.onload = draw;
function draw() {
var canvas = document.getElementById('canvas').getContext('2d');
// draw polygon points
var polygon = [
{'x':220, 'y':80},
{'x':200, 'y':180},
{'x':350, 'y':100},
{'x':30, 'y':50},
{'x':100, 'y':140},
{'x':200, 'y':10},
{'x':10, 'y':200},
{'x':150, 'y':75}
];
plen=polygon.length;
for(i=0; i<plen; i++) {
canvas.fillStyle = 'red';
canvas.fillRect(polygon[i].x-4,polygon[i].y-4,8,8);
canvas.fillStyle = 'yellow';
canvas.fillRect(polygon[i].x-2,polygon[i].y-2,4,4);
}
// draw edges
var edges = [
[[10, 200],[30, 50 ]],
[[10, 200],[100, 140]],
[[10, 200],[200, 180]],
[[30, 50 ],[100, 140]],
[[30, 50 ],[150, 75 ]],
[[30, 50 ],[200, 10 ]],
[[100, 140],[150, 75 ]],
[[100, 140],[200, 180]],
[[150, 75 ],[200, 10 ]],
[[150, 75 ],[200, 180]],
[[150, 75 ],[220, 80 ]],
[[200, 10 ],[220, 80 ]],
[[200, 10 ],[350, 100]],
[[200, 180],[220, 80 ]],
[[200, 180],[350, 100]],
[[220, 80 ],[350, 100]]
];
elen=edges.length;
canvas.beginPath();
for(i=0; i<elen; i++) {
canvas.moveTo(edges[i][0][0], edges[i][0][1]);
canvas.lineTo(edges[i][13][0], edges[i][14][1]);
}
canvas.closePath();
canvas.strokeStyle = 'blue';
canvas.stroke();
// draw center points
var points = [
[50,130],
[100,95],
[100,170],
[130,45],
[150,130],
[190,55],
[190,110],
[240,60],
[245,120]
]
plen=points.length;
for(i=0; i<plen; i++) {
canvas.fillStyle = 'black';
canvas.fillRect(points[i][0]-3,points[i][15]-3,6,6);
canvas.fillStyle = 'white';
canvas.fillRect(points[i][0]-1,points[i][16]-1,2,2);
}
// draw centroids
var centroids = [
[46.6666666667, 130.0],
[93.3333333333, 88.3333333333],
[103.333333333, 173.333333333],
[126.666666667, 45.0],
[150.0, 131.666666667],
[190.0, 55.0],
[190.0, 111.666666667],
[256.666666667, 63.3333333333],
[256.666666667, 120.0]
]
clen=centroids.length;
canvas.beginPath();
for(i=0; i<clen; i++) {
canvas.moveTo(centroids[i][0], centroids[i][17]-5);
canvas.lineTo(centroids[i][0], centroids[i][18]+5);
canvas.moveTo(centroids[i][0]-5, centroids[i][19]);
canvas.lineTo(centroids[i][0]+5, centroids[i][20]);
}
canvas.closePath();
canvas.strokeStyle = 'red';
canvas.stroke();
}
</script>
</head>
<body>
<canvas id='canvas' width="400px" height="250px"</canvas>
</body>
</html>
Это, вероятно, сделает работу. Более надежным алгоритмом для определения того, какие ребра принадлежат ячейке, было бы использование обратного метода упаковки подарков, когда ребра связаны между собой и выбор пути при разбиении будет определяться углом. Этот метод не будет восприимчив к вогнутым многоугольникам, и он будет иметь дополнительное преимущество, не полагаясь на узлы.
Это ответ @mgamba, переписанный в стиле Python. В частности, он использует itertools.cycle на точки, так что "один плюс последний пункт" может рассматриваться как первая точка более естественным образом.
import itertools as IT
def area_of_polygon(x, y):
"""Calculates the signed area of an arbitrary polygon given its verticies
http://stackru.com/a/4682656/190597 (Joe Kington)
http://softsurfer.com/Archive/algorithm_0101/algorithm_0101.htm#2D%20Polygons
"""
area = 0.0
for i in xrange(-1, len(x) - 1):
area += x[i] * (y[i + 1] - y[i - 1])
return area / 2.0
def centroid_of_polygon(points):
"""
http://stackru.com/a/14115494/190597 (mgamba)
"""
area = area_of_polygon(*zip(*points))
result_x = 0
result_y = 0
N = len(points)
points = IT.cycle(points)
x1, y1 = next(points)
for i in range(N):
x0, y0 = x1, y1
x1, y1 = next(points)
cross = (x0 * y1) - (x1 * y0)
result_x += (x0 + x1) * cross
result_y += (y0 + y1) * cross
result_x /= (area * 6.0)
result_y /= (area * 6.0)
return (result_x, result_y)
def demo_centroid():
points = [
(30,50),
(200,10),
(250,50),
(350,100),
(200,180),
(100,140),
(10,200)
]
cent = centroid_of_polygon(points)
print(cent)
# (159.2903828197946, 98.88888888888889)
demo_centroid()
Может быть, это может вам помочь: https://github.com/Bennyelg/geo_polygon_finder Этот репозиторий получает список городов и переводит их в полигоны.