Работает ли MRO или C3 линеаризация по глубине?

Question

Я читал эту статью, а затем нашел этот вопрос о стековом потоке, но в этом вопросе некоторые программисты, такие как Алекс Мартелли, сказали, что он использует подход глубины, так что теперь у меня есть большие сомнения.

Пример:

class H():
    def m(self):
        print("H")

class G(H):
    def m(self):
        print("G")
        super().m()

class I(G):
    def m(self):
        print("I")
        super().m()


class F(H):
    def m(self):
        print("F")
        super().m()

class E(H):
    def m(self):
        print("E")
        super().m()

class D(F):
    def m(self):
        print("D")
        super().m()

class C(E, F, G):
    def m(self):
        print("C")
        super().m()

class B():
    def m(self):
        print("B")
        super().m()

class A(B, C, D):
    def m(self):
        print("A")
        super().m()

x = A()
x.m()

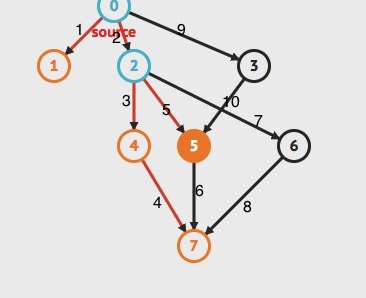
Так что, если я строю график на основе MRO, то в соответствии с глубиной сначала должно следовать следующее:

и путь должен быть:

А -> В -> С -> Е ->F->G->D-> Н

Но если вы запустите код выше, вы получите:

A
B
C
E
D
F
G
H

Потому что по этому пути:

А -> В -> С -> Е ->D->F->G-> Н

Теперь у меня путаница в отношении узла "D" или класса "D" в глубину, когда он появляется раньше, а в MRO - позже, что здесь происходит?

Answer 1

и путь должен быть:

А -> В -> С -> Е ->F->G->D-> Н

F не может прийти раньше D - это было бы противоречие - см. Класс D.

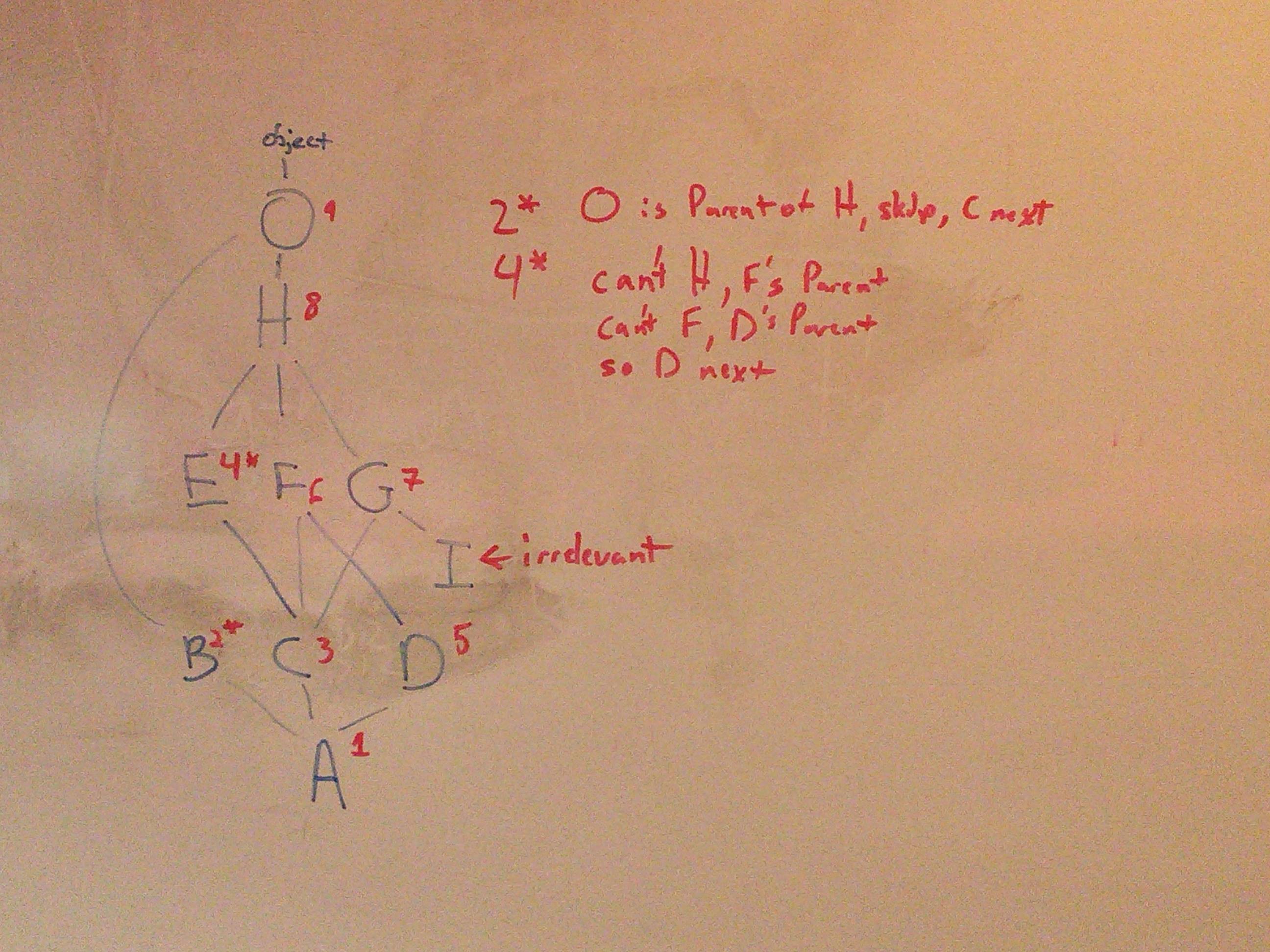
Как работает алгоритм линеаризации C3, вы должны линеаризовать родителей, а затем, если нет противоречий, вы можете линеаризовать детей. Поэтому я линеаризовал их по одному, начиная с родителей. Большинство тривиально, пока мы не дойдем до C, а затем A:

class PrettyType(type):
    def __repr__(self):
        return self.__name__

O = PrettyType('O', (object,), {})

class H(O): 'H, O, object'
# H's parent is object, assuming Python 3

class G(H): 'G, H, O, object'
# G's linearization is itself followed by its parent's linearization.

class I(G): 'I, G, H, O, object'
# I's linearization is I followed by G's

class F(H): 'F, H, O, object'

class E(H): 'E, H, O, object'

class D(F): 'D, F, H, O, object'

class C(E, F, G): 'C, E, F, G, H, O, object' 
# C's linearization is C followed by a consistent linearization of 
# its parents, left to right. 
# First C, then E - then you might be tempted to put H after E,
# but H must come after F and G (see class F and G)
# so we try F's linearization, noting that H comes after G,
# so we try G's linearization, H then consistently comes next, then object

class B(O): 'B, O, object'

А это:

class A(B, C, D): 'A, B, C, E, D, F, G, H, O, object'
# final complex case -      ^--^ can't go from E to F 
#                                D must come before F (see class D)
#                              ^--^ After D, can do F, 
#                                    then finish with C's MRO 
#                                    with no contradictions 

3 критерия, как я бы перефразировал это:

1. MRO родителей остаются последовательными
2. Местные MRO остаются неизменными
3. Нет цикличности

Алгоритм, как я бы сказал, заключается в том, что вы уважаете родителей слева направо, но сначала углубляйтесь, если не попадете к общему родителю, заблокированному ребенком (например, F заблокирован его ребенком, D), и в этом случае вы будете искать для других кандидатов (тогда D, не являясь противоречием, подойдет, тогда вы можете выбрать F и оставшуюся часть C в MRO.)

>>> A.mro()
[A, B, C, E, D, F, G, H, O, <class 'object'>]

Прямая линеаризация без линеаризации родителей в первую очередь

Мы можем работать через линеаризацию, избегая противоречий.

Снова,

• Слева направо
• Глубина первая - если общий родитель не заблокирован (должен иметь возможность вернуться)
• Циклические отношения не допускаются