Используя "Treap", чтобы сравнить два набора

Question

Я хочу использовать структуру Treap, но я плохо знаком с этим типом дерева.

У меня есть два набора, и я хочу написать метод, чтобы сравнить их с Treap. Этот метод должен возвращать значение, которое показывает сходство двух наборов. (Моя работа - извлечь набор, который в основном похож на набор ввода)

Как я могу сделать эту работу?

Спасибо

Answer 1

декартово дерево

Treap является примером сбалансированного бинарного дерева поиска (вы можете использовать любой из них для решения этой проблемы). Ожидаемая высота Treap, содержащего n элементов, равна O(logn), поскольку Treap является рандомизированной структурой данных.

Следующее решение работает для любого дерева двоичного поиска, но оно работает намного лучше, если используется сбалансированное дерево двоичного поиска (например, Treap).

Мера

Одним из показателей сходства между двумя наборами является индекс Жакара. Давайте назовем наши множества A и B. Индекс Жакара определяется как:

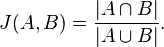
Таким образом, чтобы вычислить индекс Жакара для A и B, мы должны вычислить сумму и пересечение A и B.

операции

Давайте предположим, что A и B реализованы как сбалансированные деревья двоичного поиска.

Бинарное дерево поиска может поддерживать много операций, но для этой проблемы достаточно трех из них:

• find (x) - возвращает true, если только если x находится в дереве
• insert(x) - вставляет x в дерево, если x не было в дереве перед этой операцией
• size() - возвращает количество элементов в дереве

В сбалансированном бинарном дереве поиска найдите (x) и insert (x) время выполнения O(logn), где n - количество элементов в дереве.

Кроме того, во время вставки мы можем отслеживать размер дерева, поэтому size () может быть реализован за постоянное время.

Конечно, мы могли бы перебрать все элементы нашего Дерева.

ПСЕВДОКОД

Шаг 1.

sum(A, B):

    C = A 

    foreach x in B:
        C.insert(x)

    return C

Шаг 2.

intersection(A, B):

    C = new BalancedBinarySearchTree()

    foreach x in B:
        if(A.find(x) == true):
            C.insert(x)

    return C

Шаг 3.

Рассчитайте индекс Жакара для A и B:

JaccardIndex(A, B)
    S = sum(A, B)
    I = intersect(A, B)

    return I.size() / S.size()

сложность

Давайте предположим, что:

n = A.size()
m = B.size()

Тогда сложность вычисления суммы составляет O(n + m * log(n + m)), а сложность вычисления пересечения составляет O(m * log n).