Как получить перекрестное поведение графики Wolfram|Alpha 2D в Mathematica?

Когда курсор мыши находится над 2D-графиком в Wolfram|Alpha, появляется пара серых линий, которые помогают вам прочитать координаты по осям x и y . Например, у меня есть мышь над одной из точек поворота на следующем графике функции Эйри.

Web

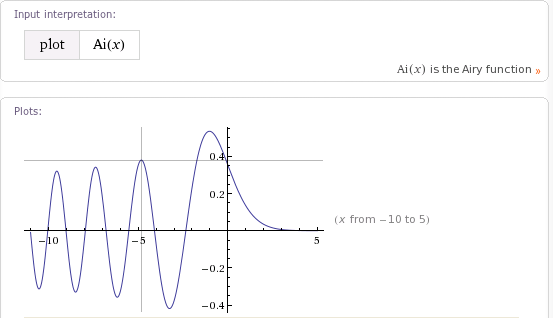
Выше также можно получить внутри Mathematica с помощью

WolframAlpha["Plot Ai(x)", {{"Plot", 1}, "Content"}]

Nb

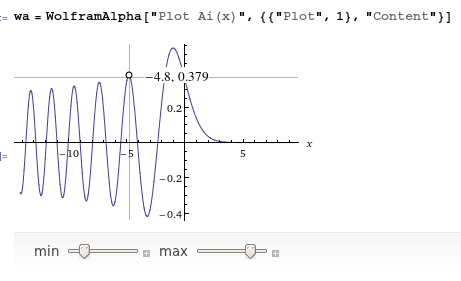
который имеет дополнительное преимущество своего рода локатора, показывающего координаты .

Как я могу подражать такому поведению в обычной графике / графике Mathematica?

Источник

4 ответа

Решение

Вот еще один подход с использованием NearestЭто немного отличается от Саймона:

plot = Plot[{Sin[x], Cos[x]}, {x, -2 Pi, 2 Pi}];
With[{nf = Nearest[Flatten[Cases[Normal[plot], Line[p_, ___] :> p, Infinity], 1]]},
   Show[plot, 
      Epilog -> 
         Dynamic[DynamicModule[{
            pt = First[nf[MousePosition[{"Graphics", Graphics}, {0, 0}]]], 
            scaled = Clip[MousePosition[{"GraphicsScaled", Graphics}, {0, 0}], {0, 1}]
            }, 
           {
            {If[scaled === None, {}, 
               {Lighter@Gray, Line[{
                   {Scaled[{scaled[[1]], 1}], Scaled[{scaled[[1]], 0}]}, 
                   {Scaled[{1, scaled[[2]]}], Scaled[{0, scaled[[2]]}]}
                   }]
               }]}, 
            {AbsolutePointSize[7], Point[pt], White, AbsolutePointSize[5], Point[pt]},
            Text[Style[NumberForm[Row[pt, ", "], {5, 2}], 12, Background -> White], Offset[{7, 0}, pt], {-1, 0}]}
         ]]
    ]
 ]

Это было сделано из примера, который я имел в виду. (Мне не нравятся свободно плавающие линии выпадения в сочетании с отслеживанием точек; либо сам по себе чувствует себя хорошо.)

Источник

Вот один с функциями, которые вы просили в комментариях:

locatorPlot[func_, r : {var_, __}, other___] :=
 LocatorPane[
   Dynamic[pos, (pos = {#, func /. var -> #}) & @@ # &],
   Column[{Plot[func, r, other], Dynamic@pos}],
   AutoAction -> True,
   Appearance ->
     Graphics[{Gray, Line @ {{{-1, 0}, {1, 0}}, {{0, -1}, {0, 1}}}},
       ImageSize -> Full]
 ]

locatorPlot[AiryAi[z], {z, -11, 5}, ImageSize -> 400]

введите описание изображения здесь

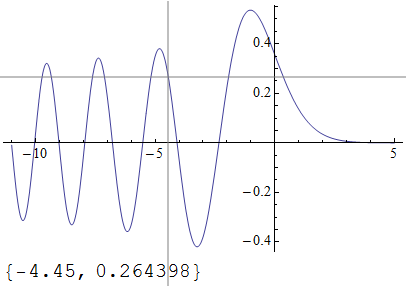
Вот довольно неуклюжее обновление для обработки ваших новых запросов:

locatorPlot[func_List, r : {var_, __}, other___] :=
 DynamicModule[{pos, pos2},
  LocatorPane[
   Dynamic[pos, (pos = #; (pos2 = {#, First@Nearest[func /. var -> #, #2]}) & @@ #) &],
   Plot[func, r, other,
     Epilog ->
      {Text[\[GrayCircle], Dynamic@pos2], Text[Dynamic@pos2, Dynamic@pos2, {-1.2, 0}]}
   ],
   AutoAction -> True,
   Appearance -> 
     Graphics[{Gray, Line@{{{-1, 0}, {1, 0}}, {{0, -1}, {0, 1}}}}, ImageSize -> Full]
   ]
  ]

locatorPlot[{AiryAi[z], Sin[z]}, {z, -11, 5}, ImageSize -> 400]
Источник

Вот моя версия, которая ведет себя аналогично выходу Wolfram|Alpha, за исключением обработки нескольких графиков. В графике W|A круг и текст переходят к ближайшей кривой и полностью исчезают, когда курсор не находится над графикой. Было бы неплохо добавить недостающую функциональность и, возможно, сделать код более гибким.

WAPlot[fns_, range : {var_Symbol, __}] := 
 DynamicModule[{pos, fn = fns},
  If[Head[fn] === List, fn = First[Flatten[fn]]];
  LocatorPane[Dynamic[pos, (pos = {var, fn} /. var -> #[[1]]) &], 
   Plot[fns, range, Method -> {"GridLinesInFront" -> True},
    GridLines->Dynamic[{{#,Gray}}&/@MousePosition[{"Graphics",Graphics},None]]],
   AutoAction -> True, 
   Appearance -> Dynamic[Graphics[{Circle[pos, Scaled[.01]], 
       Text[Framed[Row[pos, ", "], RoundingRadius -> 5, 
         Background -> White], pos, {-1.3, 0}]}]]]]

Тогда, например

WAPlot[{{AiryAi[x], -AiryAi[x]}, AiryBi[x]}, {x, -10, 2}]

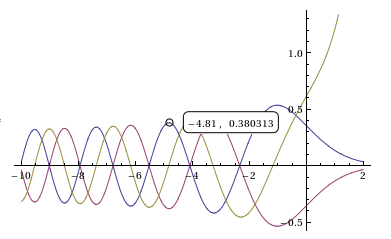
Вот новая версия, которая использует MousePosition вместо LocatorPane и крадет код мистера В., чтобы заставить круг двигаться к ближайшей кривой. Поведение теперь почти идентично WolframAlpha выход.

WAPlot[fns_, range : {var_Symbol, __}] := 
 DynamicModule[{fnList = Flatten[{fns}]}, Plot[fnList, range,
   GridLines -> 
    Dynamic[{{#, Gray}} & /@ MousePosition[{"Graphics", Graphics}]],
   Method -> {"GridLinesInFront" -> True},
   Epilog -> Dynamic[With[{mp = MousePosition[{"Graphics", Graphics}, None]},
      If[mp === None, {}, 
       With[{pos = {#1, First@Nearest[fnList /. var -> #1, #2]}& @@ mp},
        {Text[Style["\[EmptyCircle]", Medium, Bold], pos], 
         Text[Style[NumberForm[Row[pos, ", "], 2], Medium], pos, 
          {If[First[MousePosition["GraphicsScaled"]] < .5, -1.3, 1.3], 0}, 
          Background -> White]}]]]]
   ]]

Вывод выглядит очень похоже на предыдущую версию, поэтому я не буду публиковать скриншот.

Источник

От Йенс-Пира Куска:

Manipulate[myPosition = p;
 Plot[Sin[x], {x, 0, Pi}, 
  Epilog -> {Point[p], Text[p, p + {0.4, 0}]}], {{p, {0, 0}}, 
  Locator}]

От Марка МакКлюра:

labeledPointPlot[g_Graphics] := 
  Manipulate[
   Column[{Show[{g, Graphics@Point[pt]}], pt}], {pt, 
    Sequence @@ Transpose[PlotRange /. FullOptions[g]], Locator}];

labeledPointPlot[Plot[x^2, {x, -2, 2}]]

Я нашел источник кода выше, который я ранее записал:

http://www.mathkb.com/Uwe/Forum.aspx/mathematica/10416/Mathematica-6-Graphics-Options

Источник
Другие вопросы по тегам