Почему эти программы не масштабируют свою производительность от более параллельных казней?
Фон
В настоящее время я работаю над своей диссертацией бакалавра, и в основном моя задача состоит в том, чтобы оптимизировать данный код в Go, то есть сделать его максимально быстрым. Сначала я оптимизировал последовательную функцию, а затем попытался ввести параллелизм с помощью процедур. После исследования в Интернете я теперь понимаю разницу между параллелизмом и параллелизмом благодаря следующим слайдам с talk.golang. Я посетил несколько курсов параллельного программирования, где мы распараллеливали код a c/ C++ с помощью pthread/openmp, поэтому я попытался применить эти парадигмы в Go. Тем не менее, в этом конкретном случае я оптимизирую функцию, которая вычисляет скользящее среднее среза с длиной len:=n+(window_size-1) (равно 9393 или 10175), следовательно, мы имеем n окна, из которых мы вычисляем соответствующее среднее арифметическое и сохраняем его должным образом в выходном срезе.
Обратите внимание, что эта задача по своей сути смущает параллель.
Мои попытки оптимизации и результаты
В moving_avg_concurrent2 Я разделил ломтик на num_goroutines меньшие кусочки и побежал каждый с одним горутин. По какой-то причине эта функция выполнялась с одной процедурой (пока не удалось выяснить, почему, но мы тут касаемся), лучше, чем moving_avg_serial4 но с более чем одним goroutine он начал работать хуже, чем moving_avg_serial4,
В moving_avg_concurrent3 Я принял парадигму мастер / работник. Производительность была хуже чем moving_avg_serial4 при использовании одного горутина. Здесь мы по крайней мере, я получил лучшую производительность при увеличении num_goroutines но все же не лучше чем moving_avg_serial4, Чтобы сравнить выступления moving_avg_serial4, moving_avg_concurrent2 а также moving_avg_concurrent3 Я написал эталонный тест и составил таблицу результатов:
fct & num_goroutines | timing in ns/op | percentage
---------------------------------------------------------------------
serial4 | 4357893 | 100.00%
concur2_1 | 5174818 | 118.75%
concur2_4 | 9986386 | 229.16%
concur2_8 | 18973443 | 435.38%
concur2_32 | 75602438 | 1734.84%
concur3_1 | 32423150 | 744.01%
concur3_4 | 21083897 | 483.81%
concur3_8 | 16427430 | 376.96%
concur3_32 | 15157314 | 347.81%
Вопрос
Поскольку, как упоминалось выше, эта проблема смущающе параллельна, я ожидал увидеть значительное увеличение производительности, но это не так.
Почему moving_avg_concurrent2 не масштабируется вообще?
И почему moving_avg_concurrent3 намного медленнее, чем moving_avg_serial4?
Я знаю, что подпрограммы дешевы, но все еще не бесплатны, но возможно ли, что это порождает столько накладных расходов, что мы даже медленнее, чем moving_avg_serial4?
Код
Функции:
// returns a slice containing the moving average of the input (given, i.e. not optimised)
func moving_avg_serial(input []float64, window_size int) []float64 {
first_time := true
var output = make([]float64, len(input))
if len(input) > 0 {
var buffer = make([]float64, window_size)
// initialise buffer with NaN
for i := range buffer {
buffer[i] = math.NaN()
}
for i, val := range input {
old_val := buffer[int((math.Mod(float64(i), float64(window_size))))]
buffer[int((math.Mod(float64(i), float64(window_size))))] = val
if !NaN_in_slice(buffer) && first_time {
sum := 0.0
for _, entry := range buffer {
sum += entry
}
output[i] = sum / float64(window_size)
first_time = false
} else if i > 0 && !math.IsNaN(output[i-1]) && !NaN_in_slice(buffer) {
output[i] = output[i-1] + (val-old_val)/float64(window_size) // solution without loop
} else {
output[i] = math.NaN()
}
}
} else { // empty input
fmt.Println("moving_avg is panicking!")
panic(fmt.Sprintf("%v", input))
}
return output
}
// returns a slice containing the moving average of the input
// reordering the control structures to exploid the short-circuit evaluation
func moving_avg_serial4(input []float64, window_size int) []float64 {
first_time := true
var output = make([]float64, len(input))
if len(input) > 0 {
var buffer = make([]float64, window_size)
// initialise buffer with NaN
for i := range buffer {
buffer[i] = math.NaN()
}
for i := range input {
// fmt.Printf("in mvg_avg4: i=%v\n", i)
old_val := buffer[int((math.Mod(float64(i), float64(window_size))))]
buffer[int((math.Mod(float64(i), float64(window_size))))] = input[i]
if first_time && !NaN_in_slice(buffer) {
sum := 0.0
for j := range buffer {
sum += buffer[j]
}
output[i] = sum / float64(window_size)
first_time = false
} else if i > 0 && !math.IsNaN(output[i-1]) /* && !NaN_in_slice(buffer)*/ {
output[i] = output[i-1] + (input[i]-old_val)/float64(window_size) // solution without loop
} else {
output[i] = math.NaN()
}
}
} else { // empty input
fmt.Println("moving_avg is panicking!")
panic(fmt.Sprintf("%v", input))
}
return output
}
// returns a slice containing the moving average of the input
// splitting up slice into smaller pieces for the goroutines but without using the serial version, i.e. we only have NaN's in the beginning, thus hope to reduce some overhead
// still does not scale (decreasing performance with increasing size and num_goroutines)
func moving_avg_concurrent2(input []float64, window_size, num_goroutines int) []float64 {
var output = make([]float64, window_size-1, len(input))
for i := 0; i < window_size-1; i++ {
output[i] = math.NaN()
}
if len(input) > 0 {
num_items := len(input) - (window_size - 1)
var barrier_wg sync.WaitGroup
n := num_items / num_goroutines
go_avg := make([][]float64, num_goroutines)
for i := 0; i < num_goroutines; i++ {
go_avg[i] = make([]float64, 0, num_goroutines)
}
for i := 0; i < num_goroutines; i++ {
barrier_wg.Add(1)
go func(go_id int) {
defer barrier_wg.Done()
// computing boundaries
var start, stop int
start = go_id*int(n) + (window_size - 1) // starting index
// ending index
if go_id != (num_goroutines - 1) {
stop = start + n // Ending index
} else {
stop = num_items + (window_size - 1) // Ending index
}
loc_avg := moving_avg_serial4(input[start-(window_size-1):stop], window_size)
loc_avg = make([]float64, stop-start)
current_sum := 0.0
for i := start - (window_size - 1); i < start+1; i++ {
current_sum += input[i]
}
loc_avg[0] = current_sum / float64(window_size)
idx := 1
for i := start + 1; i < stop; i++ {
loc_avg[idx] = loc_avg[idx-1] + (input[i]-input[i-(window_size)])/float64(window_size)
idx++
}
go_avg[go_id] = append(go_avg[go_id], loc_avg...)
}(i)
}
barrier_wg.Wait()
for i := 0; i < num_goroutines; i++ {
output = append(output, go_avg[i]...)
}
} else { // empty input
fmt.Println("moving_avg is panicking!")
panic(fmt.Sprintf("%v", input))
}
return output
}
// returns a slice containing the moving average of the input
// change of paradigm, we opt for a master worker pattern and spawn all windows which each will be computed by a goroutine
func compute_window_avg(input, output []float64, start, end int) {
sum := 0.0
size := end - start
for _, val := range input[start:end] {
sum += val
}
output[end-1] = sum / float64(size)
}
func moving_avg_concurrent3(input []float64, window_size, num_goroutines int) []float64 {
var output = make([]float64, window_size-1, len(input))
for i := 0; i < window_size-1; i++ {
output[i] = math.NaN()
}
if len(input) > 0 {
num_windows := len(input) - (window_size - 1)
var output = make([]float64, len(input))
for i := 0; i < window_size-1; i++ {
output[i] = math.NaN()
}
pending := make(chan *Work)
done := make(chan *Work)
// creating work
go func() {
for i := 0; i < num_windows; i++ {
pending <- NewWork(compute_window_avg, input, output, i, i+window_size)
}
}()
// start goroutines which work through pending till there is nothing left
for i := 0; i < num_goroutines; i++ {
go func() {
Worker(pending, done)
}()
}
// wait till every work is done
for i := 0; i < num_windows; i++ {
<-done
}
return output
} else { // empty input
fmt.Println("moving_avg is panicking!")
panic(fmt.Sprintf("%v", input))
}
return output
}
тесты:
//############### BENCHMARKS ###############
var import_data_res11 []float64
func benchmarkMoving_avg_serial(b *testing.B, window int) {
var r []float64
for n := 0; n < b.N; n++ {
r = moving_avg_serial(BackTest_res.F["Trading DrawDowns"], window)
}
import_data_res11 = r
}
var import_data_res14 []float64
func benchmarkMoving_avg_serial4(b *testing.B, window int) {
var r []float64
for n := 0; n < b.N; n++ {
r = moving_avg_serial4(BackTest_res.F["Trading DrawDowns"], window)
}
import_data_res14 = r
}
var import_data_res16 []float64
func benchmarkMoving_avg_concurrent2(b *testing.B, window, num_goroutines int) {
var r []float64
for n := 0; n < b.N; n++ {
r = moving_avg_concurrent2(BackTest_res.F["Trading DrawDowns"], window, num_goroutines)
}
import_data_res16 = r
}
var import_data_res17 []float64
func benchmarkMoving_avg_concurrent3(b *testing.B, window, num_goroutines int) {
var r []float64
for n := 0; n < b.N; n++ {
r = moving_avg_concurrent3(BackTest_res.F["Trading DrawDowns"], window, num_goroutines)
}
import_data_res17 = r
}
func BenchmarkMoving_avg_serial_261x10(b *testing.B) {
benchmarkMoving_avg_serial(b, 261*10)
}
func BenchmarkMoving_avg_serial4_261x10(b *testing.B) {
benchmarkMoving_avg_serial4(b, 261*10)
}
func BenchmarkMoving_avg_concurrent2_261x10_1(b *testing.B) {
benchmarkMoving_avg_concurrent2(b, 261*10, 1)
}
func BenchmarkMoving_avg_concurrent2_261x10_8(b *testing.B) {
benchmarkMoving_avg_concurrent2(b, 261*10, 8)
}
func BenchmarkMoving_avg_concurrent3_261x10_1(b *testing.B) {
benchmarkMoving_avg_concurrent3(b, 261*10, 1)
}
func BenchmarkMoving_avg_concurrent3_261x10_8(b *testing.B) {
benchmarkMoving_avg_concurrent3(b, 261*10, 8)
}
//############### BENCHMARKS end ###############
Примечания:
Это мой самый первый пост, который я все еще изучаю, поэтому любая конструктивная критика также приветствуется.
1 ответ
Факт № 0: Предварительно зрелые усилия по оптимизации часто имеют отрицательный результат
показать, что это просто пустая трата времени и усилий
Зачем?
Один "неправильный" SLOC может привести к снижению производительности более чем на +37%
или может улучшить производительность, чтобы тратить менее -57% базового времени обработки
51.151µs on MA(200) [10000]float64 ~ 22.017µs on MA(200) [10000]int
70.325µs on MA(200) [10000]float64
Зачем []int -s?
Вы видите это сами по себе выше - это хлеб с маслом для HPC/fintech эффективных стратегий обработки [нами] (и мы все еще говорим с точки зрения просто [SERIAL] планирование процесса).
Этот может тестировать в любом масштабе, но лучше сначала протестировать (здесь) ваши собственные реализации, в том же масштабе - MA(200) [10000]float64 Настройка - и опубликуйте ваши базовые длительности в [us] просмотреть начальную производительность процесса и сравнить яблоки с яблоками, разместив 51.2 [us] порог для сравнения.
Далее идет более сложная часть:
Факт № 1: эта задача НЕ смущающе параллельна
Да, можно пойти и реализовать вычисление скользящего среднего, чтобы оно действительно проходило через кучи данных, используя некоторое намеренно внушаемое "просто"- [CONCURRENT] подход к обработке (независимо от того, происходит ли это из-за какой-то ошибки, "совета" какого-то авторитета, профессиональной слепоты или просто из-за справедливого невежества двойного Сократа), что, очевидно, не означает, что характер сверточной потоковой обработки, присутствующий внутри Скользящая средняя математическая формулировка, забыл быть чистым [SERIAL] процесс, просто из-за попытки обеспечить его выполнение рассчитывается в некоторой степени "просто"- [CONCURRENT] обработка.
(Кстати. Жесткие компьютерные ученые и ботаники с двумя доменами также будут возражать здесь, что языком Go является дизайн, использующий лучшие навыки Роба Пайка для создания структуры параллельных сопрограмм, а не какой-либо истинной [PARALLEL] планирование процессов, даже несмотря на то, что CSP-инструменты Hoare, доступные в концепции языка, могут добавить немного соли и перца и внедрить средства межпроцессного взаимодействия типа "стоп-блок", которые будут блокировать "просто"- [CONCURRENT] фрагменты кода в некоторой аппаратной CSP-p2p-синхронизации.)
Факт № 2: Распространяйся (для любого ускорения) только НА КОНЦЕ
Низкий уровень производительности в [SERIAL] не устанавливает никакого критерия. Имея разумное количество настроек производительности в однопоточном режиме, только тогда можно получить выгоду от распределения (по-прежнему приходится оплачивать дополнительные серийные расходы, что заставляет вступить в игру закон Амдаля (скорее, строгий закон Амдала)).
Если можно ввести такой низкий уровень дополнительных затрат на установку и при этом достичь какого-либо замечательного параллелизма, масштабируемого на [SEQ] Часть обработки, там и только там появляется шанс повысить эффективность процесса.
Нетрудно потерять гораздо больше, чем выиграть, поэтому всегда проверяйте чистоту [SEQ] против потенциальных компромиссов между non-[SEQ] / N[PAR]_processes теоретическое ускорение, за которое нужно заплатить сумму суммы всех дополнительных [SEQ] накладные расходы, если и только если:
( pure-[SEQ]_processing [ns]
+ add-on-[SEQ]-setup-overheads [ns]
+ ( non-[SEQ]_processing [ns] / N[PAR]_processes )
) << ( pure-[SEQ]_processing [ns]
+ ( non-[SEQ]_processing [ns] / 1 )
)
Не имея такого преимущества для реактивных истребителей, как избыточная высота и Солнце позади вас, никогда не пытайтесь делать какие-либо попытки HPC / распараллеливания - они никогда не окупятся, не будучи замечательно << лучше, чем умный [SEQ] -процесс.
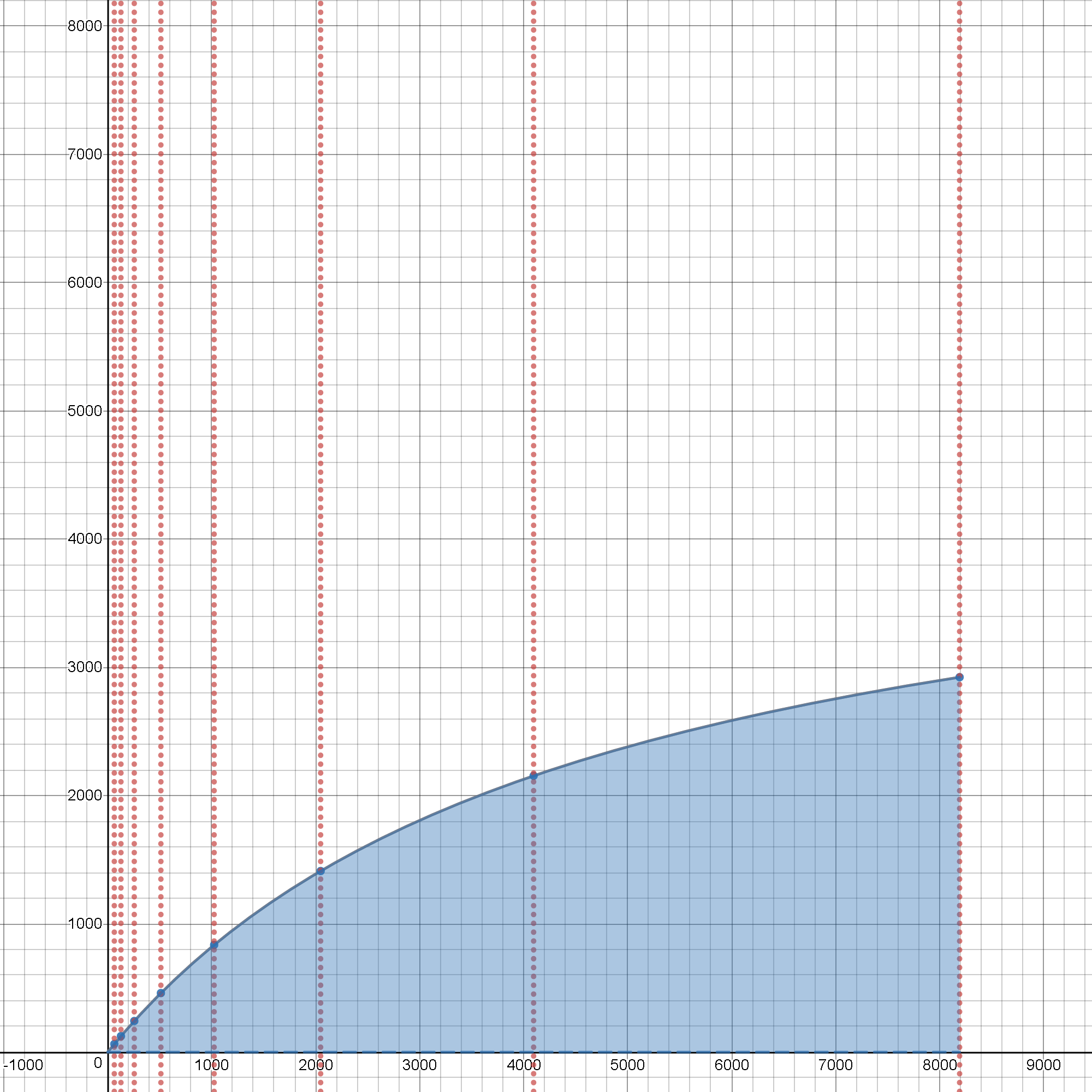
Эпилог: на интерактивном эксперименте UI-строгого закона Амдала
Одна анимация стоит миллион слов.
Интерактивная анимация еще лучше:
Так,
принять тестируемый процесс, который имеет как [SERIAL] и [PARALLEL] часть графика процесса.
Позволять p быть [PARALLEL] доля длительности процесса ~ ( 0.0 .. 1.0 ) Таким образом [SERIAL] часть не длится дольше чем ( 1 - p ), право?
Итак, давайте начнем интерактивные эксперименты с такого теста, где p == 1.0Это означает, что вся такая продолжительность процесса тратится всего на [PARALLEL] часть, и как начальный последовательный, так и завершающие части потока процесса (которые, как правило, всегда [SERIAL]) имеют нулевую продолжительность ( ( 1 - p ) == 0. )
Предположим, что система не обладает какой-то особой магией и поэтому должна потратить некоторые реальные шаги на инициализацию каждого из [PARALLEL] часть, чтобы запустить его на другом процессоре ( (1), 2, .., N ) Итак, давайте добавим некоторые накладные расходы, если будет предложено реорганизовать поток процесса и выполнить маршалирование + распространение + отмену маршалинга всех необходимых инструкций и данных, чтобы намеченный процесс теперь мог запускаться и выполняться N Процессоры параллельно.
Эти расходы называются o (здесь изначально предполагается, что для простоты, чтобы быть просто постоянным и инвариантным N, что не всегда имеет место в реальном времени, на кремнии / на NUMA / на распределенных инфраструктурах).
Если щелкнуть заголовок "Эпилог" выше, откроется интерактивная среда, в которой можно бесплатно экспериментировать.
С p == 1. && o == 0. && N > 1 производительность круто растет до текущей достижимой [PARALLEL] - аппаратные ограничения O/S для все еще монолитного выполнения кода O/S (где по-прежнему нет дополнительных затрат на распространение для MPI- и аналогичных распределений рабочих модулей в режиме depeche-режима (где нужно было бы сразу добавить действительно большое количество [ms] в то время как наш пока лучший просто [SERIAL] реализация, очевидно, сделала всю работу менее чем за ~ 22,1 [нас])).
Но кроме такого искусственно оптимистичного случая, работа не выглядит настолько дешевой, чтобы ее можно было эффективно распараллелить.
Попробуйте иметь не ноль, а только ~ 0,01% накладных расходов на установку
oи линия начинает показывать совершенно иную природу масштабируемого с учетом накладных расходов масштабирования даже для крайней степени[PARALLEL]дело (имея ещеp == 1.0) и иметь потенциальное ускорение где-то около половины изначально супер-идеалистического случая линейного ускорения.Теперь включите
pк чему-то ближе к реальности, где-то менее искусственно установленный, чем первоначальный супер-идеалистический случай== 1.00--> { 0.99, 0.98, 0.95 }и ... бинго, это реальность, где планирование процесса должно быть проверено и предварительно проверено.
Что это значит?
В качестве примера, если бы издержки (на запуск + окончательное присоединение к пулу сопрограмм) заняли бы больше ~ 0.1% фактического [PARALLEL] при длительности секции обработки не будет большего ускорения в 4 раза (примерно 1/4 от первоначальной продолжительности во времени) для 5 сопрограмм (с p ~ 0,95), не более чем в 10 раз (в 10 раз быстрее) для 20 сопрограмм (все при условии, что система имеет 5-ядерные ядра, соответственно 20-ядерные процессоры свободны и доступны и готовы (лучше всего с процессами / потоками, сопоставленными с привязкой к CPU-core-уровням уровня O/S) для бесперебойного обслуживания всех этих сопрограмм во время весь их жизненный цикл, чтобы достичь любого ожидаемого ускорения.
Отсутствие такого количества аппаратных ресурсов, свободных и готовых для всех тех целевых блоков, предназначенных для реализации [PARALLEL] -часть графика процесса, состояния блокировки / ожидания будут вводить дополнительные абсолютные состояния ожидания, а результирующая производительность добавляет эти новые [SERIAL] -блокирование / ожидание разделов общей продолжительности процесса и первоначально желаемого ускорения внезапно прекращают существовать, и коэффициент производительности значительно падает << 1.00 (Это означает, что эффективное время выполнения было связано с тем, что состояния блокировки были медленнее, чем непараллельные [SERIAL] рабочий процесс).
Это может показаться сложным для новых увлеченных экспериментаторов, однако мы можем поставить это в обратную сторону. Учитывая весь процесс распространения предполагаемого [PARALLEL] известно, что пул задач не короче, чем, скажем, 10 [us] На графиках строгих издержек должно быть не менее 1000 x 10 [us] неблокирующих вычислений интенсивной обработки внутри [PARALLEL] раздел, чтобы не опустошать эффективность параллельной обработки.
Если нет достаточно "жирной" части обработки, накладные расходы (значительно превышающие приведенный выше порог ~ 0.1%) затем жестоко опустошить чистую эффективность успешно распараллеленной обработки (но выполнив при таких неоправданно высоких относительных затратах на установку против ограниченных чистых эффектов любого N -процессоры, как было продемонстрировано в доступных live-графиках).
Для любителей распределенных вычислений нет ничего удивительного в том, что o поставляется также с дополнительными зависимостями - на N (чем больше процессов, тем больше усилий нужно потратить на распространение рабочих пакетов), на размеры распределенных BLOB-объектов данных (чем больше BLOB, тем дольше блоки MEM-/IO-устройств остаются заблокированными, прежде чем обслуживать следующий процесс для получить распределенный BLOB по такому устройству / ресурсу для каждого целевого объекта 2..N -го процесса приема), по предотвращенным / сигнализированным CSP, опосредованным каналом межпроцессным координированию (назовите это дополнительной блокировкой для каждого инцидента, уменьшая p все дальше и дальше ниже, в конечном счете, хорошего идеала 1.).
Таким образом, реальность реального мира весьма далека от изначально идеализированной, красивой и многообещающей. p== 1.0, ( 1 -p) == 0.0 а также o== 0.0
Как очевидно с самого начала, попробуйте побить 22.1 [us][SERIAL] порог, чем пытаться обойти это, пока все хуже и хуже, если собираешься [PARALLEL] где реалистичные издержки и масштабирование, используя уже недостаточно эффективные подходы, не помогают ни на секунду.