Когда использовать трепан

Question

Когда использовать трепан

Может ли кто-нибудь привести реальные примеры того, когда лучшим способом хранения ваших данных является treap?

Я хочу понять, в каких ситуациях трэп будет лучше, чем кучи и древовидные структуры.

Если это возможно, приведите несколько примеров из реальных ситуаций.

Я пытался найти случаи использования треппов здесь и путем поиска в Google, но ничего не нашел.

Спасибо.

28

data-structures treap cartesian-tree

Источник

user2281439 15 апр '13 в 06:57

6 ответов

Другие вопросы по тегам data-structures treap cartesian-tree

user2013916 27 авг '13 в 08:00 2013-08-27 08:00 · Answer 1 · 2013-08-27 08:00

Если значения хеш-функции используются в качестве приоритетов, трепа предоставляют уникальное представление контента.

Рассмотрим набор порядка элементов, реализованный в виде AVL-дерева или rb-дерева. Вставка предметов в разных порядках, как правило, заканчивается деревьями различной формы (хотя все они сбалансированы). Для данного контента треп всегда будет иметь одинаковую форму независимо от истории.

Я видел две причины, почему уникальное представление может быть полезным:

Причины безопасности. Трепа не может содержать информацию об истории.
Эффективное совместное использование поддерева. Самые быстрые алгоритмы для операций над множествами, которые я видел, используют трепы.

user533480 15 апр '13 в 07:14 2013-04-15 07:14 · Answer 2 · 2013-04-15 07:14

Я не могу предоставить вам никаких реальных примеров. Но я использую трепы для решения некоторых проблем в соревнованиях по программированию:

На самом деле это не настоящие проблемы, но они имеют смысл.

8

Источник

user533480 15 апр '13 в 07:14

user328616 15 апр '13 в 10:06 2013-04-15 10:06 · Answer 3 · 2013-04-15 10:06

Вы можете использовать его как реализацию карты на основе дерева. В зависимости от приложения, это может быть быстрее. Пару лет назад я сам реализовал Treap и Skip list (на Java) для развлечения и провел базовый сравнительный анализ, сравнивая их с TreeMap, и Treap оказался самым быстрым. Вы можете увидеть результаты здесь.

Одним из его главных преимуществ является то, что его очень легко реализовать, по сравнению, например, с красно-черными деревьями. Однако, насколько я помню, он не имеет гарантированных затрат на свои операции (поиск - O(log n) с high вероятность), по сравнению с красно-черными деревьями, что означает, что вы не сможете использовать его в критически важных для безопасности приложениях, где требуется конкретный срок.

user2548019 18 авг '13 в 20:05 2013-08-18 20:05 · Answer 4 · 2013-08-18 20:05

Treaps - это отличный вариант сбалансированного бинарного дерева поиска. Существует множество алгоритмов для балансировки бинарных деревьев, но большинство из них - ужасные вещи с тоннами особых случаев, которые нужно обрабатывать. С другой стороны, очень легко кодировать Treaps. При некотором использовании случайности у нас есть BBT, который, как ожидается, будет иметь логарифмическую высоту. Вот некоторые хорошие проблемы, которые нужно решить с помощью треппов: http://www.spoj.com/problems/QMAX3VN/ (простой уровень) http://www.spoj.com/problems/GSS6/ (средний уровень)

user10262805 22 окт '21 в 05:06 2021-10-22 05:06 · Answer 5 · 2021-10-22 05:06

Допустим, у вас есть компания, и вы хотите создать инструмент инвентаризации:

Уметь (эффективно) искать товары по названию, чтобы вы могли обновлять ассортимент.
Получите в любое время продукт с наименьшим количеством товаров на складе, чтобы вы могли спланировать свой следующий заказ.

Один из способов удовлетворить эти требования может заключаться в использовании двух разных структур данных: одной для эффективного поиска по имени, например, хэш-таблицы, и очереди с приоритетами для получения элемента, который необходимо срочно пополнить. Вам необходимо согласовать эти две структуры данных, и вам потребуется более чем в два раза больше памяти. если мы отсортируем список записей по имени, нам нужно просканировать весь список, чтобы найти заданное значение для другого критерия, в данном случае количества на складе. Кроме того, если мы используем минимальную кучу с более редкими продуктами наверху, нам потребуется линейное время для сканирования всей кучи в поисках продукта для обновления.

Treap

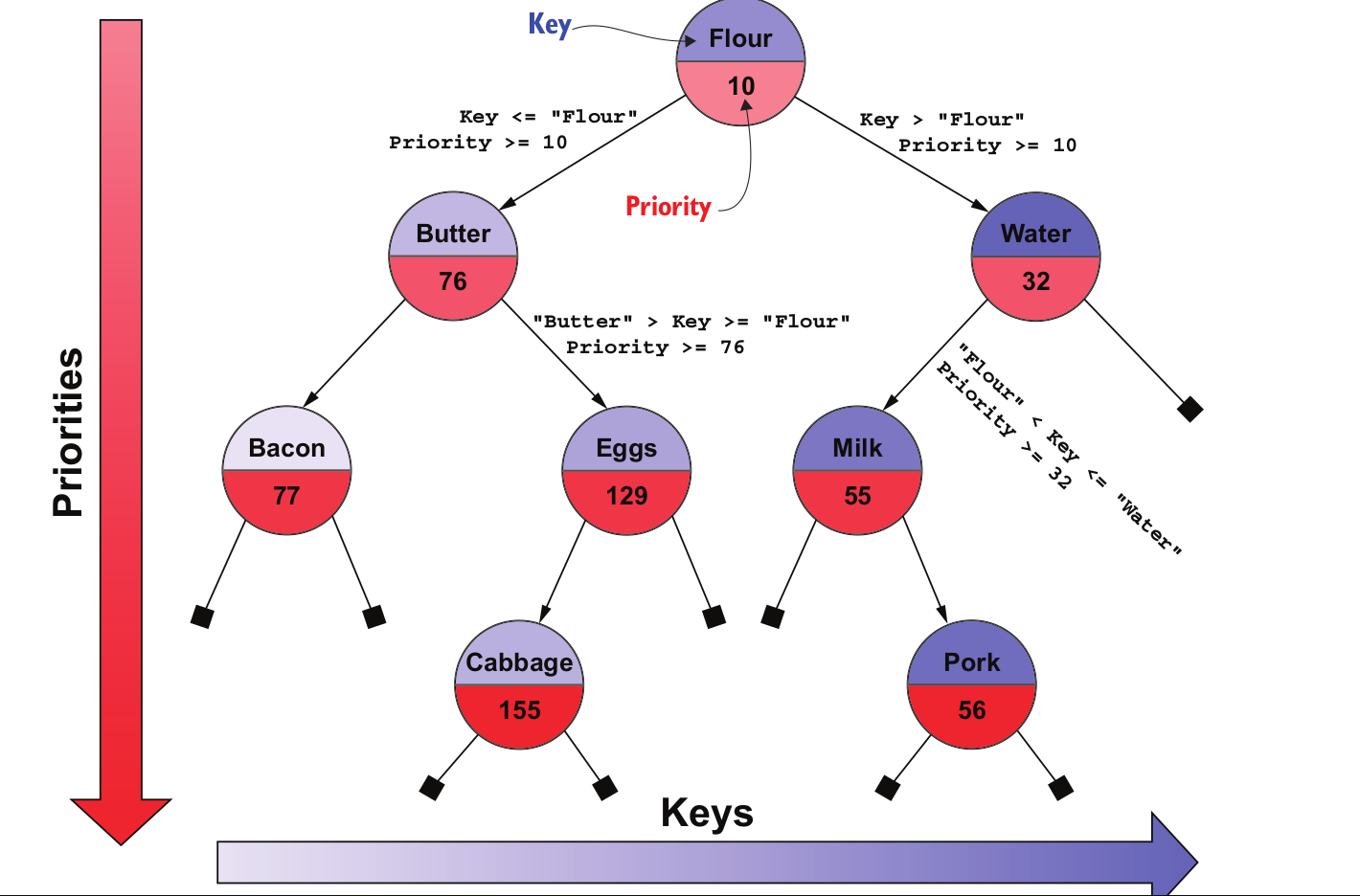
Treap - это смесь дерева и кучи. Идея состоит в том, чтобы наложить ограничения BST на имена и ограничения кучи на количество.

Названия продуктов рассматриваются как ключи двоичного дерева поиска.

Объемы запасов, напротив, рассматриваются как приоритеты кучи, поэтому они определяют частичное упорядочение сверху вниз. Для приоритетов, как и для всех куч, у нас есть частичный порядок, что означает, что только узлы на одном пути от корня до листьев упорядочиваются в соответствии с их приоритетом. На изображении выше вы можете видеть, что дочерние узлы всегда имеют большее количество запасов, чем их родительские, но нет никакого упорядочивания между братьями и сестрами.

user3642994 19 дек '21 в 02:02 2021-12-19 02:02 · Answer 6 · 2021-12-19 02:02

Любое поддерево в Treap также является Treap (т.е. удовлетворяет правилу BST, а также правилу минимальной или максимальной кучи). Благодаря этому свойству упорядоченный список можно легко разделить, или несколько упорядоченных списков можно легко объединить с помощью Treaps, чем с помощью дерева RB. Реализация проще. Дизайн тоже проще.