Сравнение графиков с ограничениями

Question

У меня есть эта проблема ниже, и я не вижу эффективного решения, но использую метод грубой силы. Кто-нибудь мог бы протянуть мне руку?

Задача состоит из графа G= (V,E), направленного, взвешенного и ациклического. Края имеют веса w(u,v). Значение w (u, v) зависит только от вершины происхождения (w (u, x) = w (u, y), если (u,x) и (u,y) существуют). Первоначально каждая вершина может иметь несколько входящих и / или исходящих ребер. Цель состоит в том, чтобы максимально поддерживать один исходящий край на вершину таким образом, чтобы общий оставшийся вес был максимальным. Вершины с исходящими ребрами не могут иметь входящие. Например, рассмотрим рисунок 1. Левый график является исходным. Сохраняя не более одного исходящего ребра, правый график представляет решение для максимального общего веса, 17.

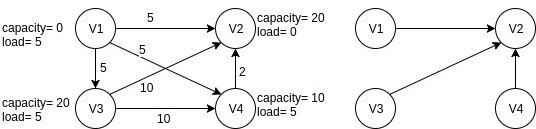
Однако есть еще одно ограничение для этой проблемы. Каждой вершине присваивается 2 значения, емкость и нагрузка. Емкость говорит о том, какую нагрузку он может прикрепить. Грузоподъемность также должна учитываться при поиске максимальной общей массы конфигурации. На рисунке 2 показан тот же график, что и на рисунке 1, но теперь ограничение емкости играет решающую роль. Обратите внимание, что конфигурация максимального общего веса в этой ситуации отличается (график справа, рисунок 2).

Таким образом, есть 3 ограничения для получения максимального общего веса:

1. Соблюдайте ограничения по пропускной способности;
2. Вершины с исходящим ребром не имеют входящих;
3. У вершин максимум одно исходящее ребро.

Единственное решение, которое я придумала, - это тестирование всех возможных конфигураций, проверка их корректности и отслеживание максимума. У кого-нибудь есть лучший подход к решению этой проблемы?

Answer 1

Ваша проблема для меня выглядит как проблема ранца: подберите набор ребер, чтобы максимизировать прибыль.

Что вы можете сделать наверняка, так это использовать подход удовлетворения ограничений. Например, проверьте этот код, который решает проблему ранца. Адаптировать его к вашим потребностям должно быть довольно простой задачей.

Вам не нужен какой-либо алгоритм сопоставления с этим подходом - процедура решения создаст наилучшее возможное решение напрямую. Тем не менее, это может занять много времени / памяти для больших графиков (тысячи ребер / узлов).