Спиральная петля на матрице из точки
У меня есть двумерная сетка, как показано ниже, и я хочу начать с X, Y и сохранить угол окна (W) и перекрытие (OP). Я пробовал эти коды, но ни один из них не подходит для моей цели.
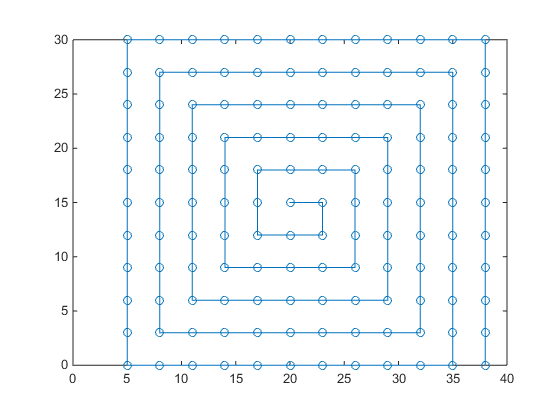
Как показано, я хочу начать со случайной точки (черная ячейка) и сохранить угловые положения (показанные черными кружками) каждого нового окна в спиральной петле. Алгоритм должен использоваться для любых размеров сетки (не обязательно квадратной) и для любых начальных точек.
Matlab также имеет функцию (спираль), которая похожа на то, что я хочу, но она не принимает сетку, размер окна и перекрытия (OP).
Я ожидаю получить следующий результат для этой цифры: (8,12) (11,12) (11,9) (8,9) (4,9) (4,12) (4,15) ...
Я использую следующие коды, которые начинаются с угла и постепенно заполняют матрицу, используя определенные размеры W, OP и Matrix:
W = [10 12];
OP = [4 3];
M = zeros(100,110);
for i=[1:W(1)-OP(1):size(M,1)-W(1), size(M,1)-W(1)+1]
for j=[1:W(2)-OP(2):size(M,2)-W(2), size(M,2)-W(2)+1]
block = rand(W(1),W(2));
M(i:i+W(1)-1, j:j+W(2)-1) = block;
imagesc(M); axis equal tight xy
pause(.1)
end;
end;
Итак, более понятным образом, как я должен изменить код "выше", чтобы начать с местоположения (x,y) и по спирали заполнить всю матрицу в соответствии с W, OP и размером (M).
Спасибо!
2 ответа
Вот фрагмент кода, который производит ожидаемый результат. Там, где только незначительные изменения в spiral_generic необходимы, чтобы соответствовать вашим требованиям:
function demo()
spiral_generic([10,11],[3,4])
W = [10 12];
OP = [4 3];
%make sure your start point is really on the grid of r and c, this is not checked!
start = [19,28];
M = zeros(100,110);
r=[1:W(1)-OP(1):size(M,1)-W(1), size(M,1)-W(1)+1];
c=[1:W(2)-OP(2):size(M,2)-W(2), size(M,2)-W(2)+1];
startindex=[find(r==start(1),1,'first'),find(c==start(2),1,'first')];
A=spiral_generic([numel(r),numel(c)],startindex);
[~,idx]=sort(A(:));
[ridx,cidx]=ind2sub(size(A),idx);
%blocks contains the lower left corners in order of processing.
blocks=[r(ridx);c(cidx)];
for blockindex=blocks
block = rand(W(1),W(2));
M(blockindex(1):blockindex(1)+W(1)-1, blockindex(2):blockindex(2)+W(2)-1) = block;
imagesc(M);
pause(.1)
end
end
function A = spiral_generic(n, P)
% Makes NxN matrix filled up spirally starting with point P
r = max([P - 1, n - P]); % Radius of the bigger matrix
M = spiral(2 * r + 1); % Bigger matrix itself
M = permute(M,[2,1]); % changing start direction of the spiral
M = M(:,end:-1:1); % chaning spin orientation
C = r + 1 - (P - 1); % Top-left corner of A in M
A = M(C(1):C(1)+n(1)-1, C(2):C(2)+n(2)-1); % Get the submatrix
[~, order] = sort(A(:)); % Get elements' order
A(order) = 1:(n(1)*n(2)); % Fill with continous values
end
Основная проблема
Пусть данные будут определены как:
step = 3; %// step size
x0 = 8; %// x coordinate of origin
y0 = 12; %// y coordinate of origin
N = 32; %// number of steps
Тогда координаты спирали можно получить в виде значений в комплексной плоскости следующим образом †:
z = x0+1j*y0 + step*cumsum([0 -1j.^(-floor(sqrt(4*(0:N)+1))-1)]);
Конечно, координаты х и у тогда
x = real(z);
y = imag(z);
С примерами значений, приведенных выше, plot(z,'o-') (или же plot(x,y,'o-')) производит график
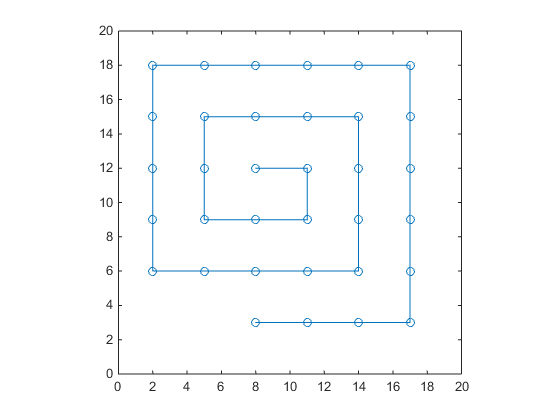
† Ключ должен был создать последовательность 1,2,3,3,4,4,5,5,5,6,6,6,7,7,7,7,8,8,8,8... Я в долгу перед OEIS за решение этой части. Последовательность оказывается целой частью квадратного корня из 4n+1, для n=1,2,3,...
Как включить перекрытие и размер окна
Чтобы принять во внимание совпадение, следуя предложению Дэниела, вычтите его значение из step,
Чтобы рассмотреть размер окна, N должен быть достаточно большим, чтобы спираль доходила до некоторой точки за пределами границы окна; и тогда будут сохранены только предыдущие пункты.
Поскольку заранее сложно вычислить, насколько велика N должно быть, один из возможных подходов заключается в экспоненциальном увеличении N в цикле, пока он не станет достаточно большим. Экспоненциальное увеличение гарантирует, что число итераций цикла будет небольшим. Код ниже использует степени 2 для N,
%// Data
step = 3; %// step size
overlap = 1; %// overlap
x0 = 20; %// x coordinate of origin
y0 = 15; %// y coordinate of origin
xmin = 0; %// window boundary: min x
xmax = 40; %// window boundary: max x
ymax = 30; %// window boundary: min y
ymin = 0; %// window boundary: max y
%// Computations
stepov = step-overlap;
N = 8; %// Initial value. Will be increased as needed
done = false;
while ~done
z = x0+1j*y0 + stepov*cumsum([0 -1j.^(-floor(sqrt(4*(0:N)+1))-1)]);
%// compute coordinates of N points
ind = find(real(z)<xmin | real(z)>xmax | imag(z)<ymin | imag(z)>ymax, 1);
%// find index of first z out of boundary, if any
done = ~isempty(ind); %// exit if we have reached outside window boundary
N = N*2; %// increase number of steps for next try
end
z = z(1:ind-1); %// only keep values that are within the boundary
x = real(z);
y = imag(z);
С данными, указанными в коде, полученный график выглядит следующим образом. Обратите внимание, что последняя точка (38,0). Следующая точка будет (38,-2), которая находится за границей окна.