Записанный звук одной ноты производит несколько раз начала

Question

Я использую библиотеку Librosa для определения высоты тона и появления. В частности, я использую onset_detect а также piptrack,

Это мой код:

def detect_pitch(y, sr, onset_offset=5, fmin=75, fmax=1400):
  y = highpass_filter(y, sr)

  onset_frames = librosa.onset.onset_detect(y=y, sr=sr)
  pitches, magnitudes = librosa.piptrack(y=y, sr=sr, fmin=fmin, fmax=fmax)

  notes = []

  for i in range(0, len(onset_frames)):
    onset = onset_frames[i] + onset_offset
    index = magnitudes[:, onset].argmax()
    pitch = pitches[index, onset]
    if (pitch != 0):
      notes.append(librosa.hz_to_note(pitch))

  return notes

def highpass_filter(y, sr):
  filter_stop_freq = 70  # Hz
  filter_pass_freq = 100  # Hz
  filter_order = 1001

  # High-pass filter
  nyquist_rate = sr / 2.
  desired = (0, 0, 1, 1)
  bands = (0, filter_stop_freq, filter_pass_freq, nyquist_rate)
  filter_coefs = signal.firls(filter_order, bands, desired, nyq=nyquist_rate)

  # Apply high-pass filter
  filtered_audio = signal.filtfilt(filter_coefs, [1], y)
  return filtered_audio

При запуске этого сэмпла на гитаре, записанного в студии, поэтому сэмплы без шума (как этот), я получаю очень хорошие результаты в обеих функциях. Время начала правильное, а частоты почти всегда правильные (иногда с некоторыми октавными ошибками).

Однако, большая проблема возникает, когда я пытаюсь записать свои собственные звуки гитары с помощью моего дешевого микрофона. Я получаю аудио файлы с шумом, такие как этот. onset_detect алгоритм запутывается и думает, что шум содержит время начала. Поэтому я получаю очень плохие результаты. Я получаю много раз, даже если мой аудиофайл состоит из одной заметки.

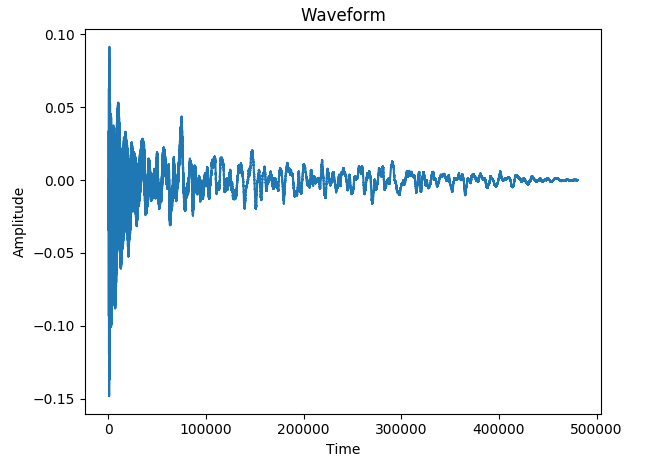
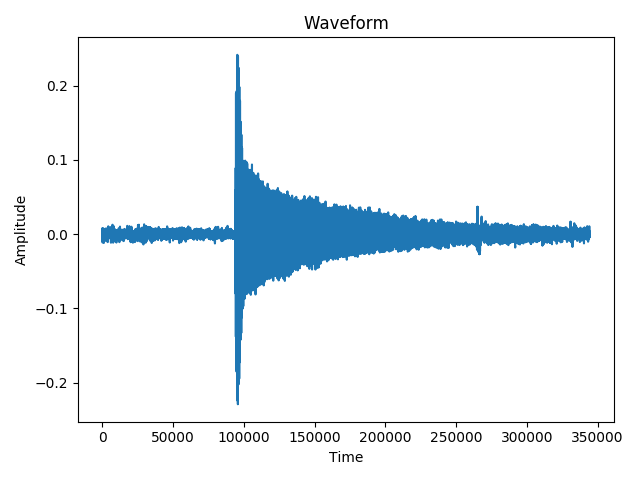
Вот две формы волны. Первый - это гитарный образец ноты B3, записанный в студии, а второй - моя запись ноты E2.

Результатом первого является правильно B3 (было обнаружено время начала). Результатом второго является массив из 7 элементов, что означает, что было обнаружено 7 времен начала вместо 1! Одним из этих элементов является правильное время начала, другие элементы - просто случайные пики в шумовой части.

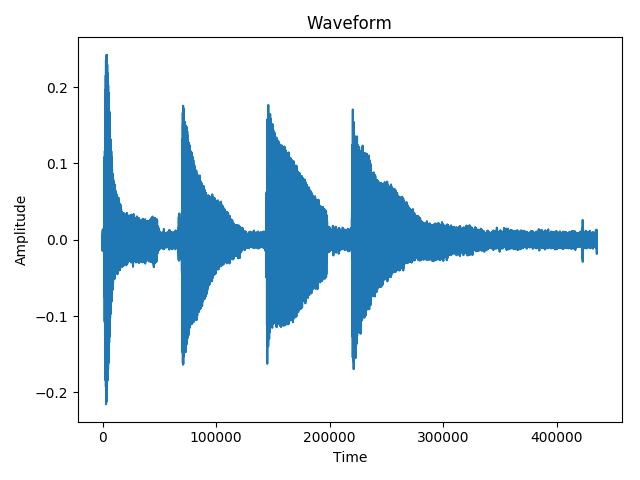
Другим примером является этот аудиофайл, содержащий примечания B3, C4, D4, E4:

Как вы можете видеть, шум ясен, и мой фильтр верхних частот не помог (это форма волны после применения фильтра).

Я предполагаю, что это вопрос шума, поскольку разница между этими файлами лежит там. Если да, что я могу сделать, чтобы уменьшить его? Я пытался использовать фильтр верхних частот, но без изменений.

Answer 1

У меня есть три замечания, которыми можно поделиться.

Во-первых, после небольшой игры, я пришел к выводу, что алгоритм обнаружения начала выглядит так, как будто он, вероятно, предназначен для автоматического изменения масштаба своей собственной операции, чтобы учесть локальный фоновый шум в любой момент времени. Это, вероятно, для того, чтобы он мог определять время начала в секциях пианиссимо с равной вероятностью, как это было бы в секциях фортиссимо. Это приводит к неудачному результату, когда алгоритм имеет тенденцию вызывать фоновые шумы, исходящие от вашего дешевого микрофона - алгоритм обнаружения начала искренне считает, что он просто слушает музыку пианиссимо.

Второе наблюдение заключается в том, что примерно первые ~2200 выборок в вашем записанном примере (примерно первые 0,1 секунды) немного шатки, в том смысле, что шум действительно равен нулю в течение этого короткого начального интервала. Попробуйте увеличить масштаб сигнала в начальной точке, и вы поймете, что я имею в виду. К сожалению, начало игры на гитаре следует так быстро после появления шума (примерно около образца 3000), что алгоритм не может разрешить два независимо друг от друга - вместо этого он просто объединяет два в одно событие начала, которое также начинается примерно через 0,1 секунды. рано. Поэтому я вырезал примерно первые 2240 сэмплов, чтобы "нормализовать" файл (хотя я не думаю, что это мошенничество; это краевой эффект, который, вероятно, исчезнет, ​​если вы просто записали секунду или около того первоначального молчания до выщипывание первой строки, как обычно)

Мое третье наблюдение состоит в том, что частотная фильтрация работает, только если шум и музыка на самом деле находятся в несколько разных частотных диапазонах. Это может быть правдой в этом случае, однако я не думаю, что вы это продемонстрировали. Поэтому вместо частотной фильтрации я решил попробовать другой подход: пороговое значение. Я использовал последние 3 секунды вашей записи, когда гитара не играла, чтобы оценить типичный уровень фонового шума на протяжении всей записи, в единицах среднеквадратичной энергии, а затем я использовал это медианное значение, чтобы установить минимальный порог энергии, который был рассчитан, чтобы лежать безопасно выше среднего. Только начальные события, возвращаемые детектором в моменты, когда среднеквадратичная энергия превышает пороговое значение, принимаются как "действительные".

Пример скрипта показан ниже:

import librosa
import numpy as np
import matplotlib.pyplot as plt

# I played around with this but ultimately kept the default value
hoplen=512

y, sr = librosa.core.load("./Vocaroo_s07Dx8dWGAR0.mp3")
# Note that the first ~2240 samples (0.1 seconds) are anomalously low noise,
# so cut out this section from processing
start = 2240
y = y[start:]
idx = np.arange(len(y))

# Calcualte the onset frames in the usual way
onset_frames = librosa.onset.onset_detect(y=y, sr=sr, hop_length=hoplen)
onstm = librosa.frames_to_time(onset_frames, sr=sr, hop_length=hoplen)

# Calculate RMS energy per frame.  I shortened the frame length from the
# default value in order to avoid ending up with too much smoothing
rmse = librosa.feature.rmse(y=y, frame_length=512, hop_length=hoplen)[0,]
envtm = librosa.frames_to_time(np.arange(len(rmse)), sr=sr, hop_length=hoplen)
# Use final 3 seconds of recording in order to estimate median noise level
# and typical variation
noiseidx = [envtm > envtm[-1] - 3.0]
noisemedian = np.percentile(rmse[noiseidx], 50)
sigma = np.percentile(rmse[noiseidx], 84.1) - noisemedian
# Set the minimum RMS energy threshold that is needed in order to declare
# an "onset" event to be equal to 5 sigma above the median
threshold = noisemedian + 5*sigma
threshidx = [rmse > threshold]
# Choose the corrected onset times as only those which meet the RMS energy
# minimum threshold requirement
correctedonstm = onstm[[tm in envtm[threshidx] for tm in onstm]]

# Print both in units of actual time (seconds) and sample ID number
print(correctedonstm+start/sr)
print(correctedonstm*sr+start)

fg = plt.figure(figsize=[12, 8])

# Print the waveform together with onset times superimposed in red
ax1 = fg.add_subplot(2,1,1)
ax1.plot(idx+start, y)
for ii in correctedonstm*sr+start:
    ax1.axvline(ii, color='r')
ax1.set_ylabel('Amplitude', fontsize=16)

# Print the RMSE together with onset times superimposed in red
ax2 = fg.add_subplot(2,1,2, sharex=ax1)
ax2.plot(envtm*sr+start, rmse)
for ii in correctedonstm*sr+start:
    ax2.axvline(ii, color='r')
# Plot threshold value superimposed as a black dotted line
ax2.axhline(threshold, linestyle=':', color='k')
ax2.set_ylabel("RMSE", fontsize=16)
ax2.set_xlabel("Sample Number", fontsize=16)

fg.show()

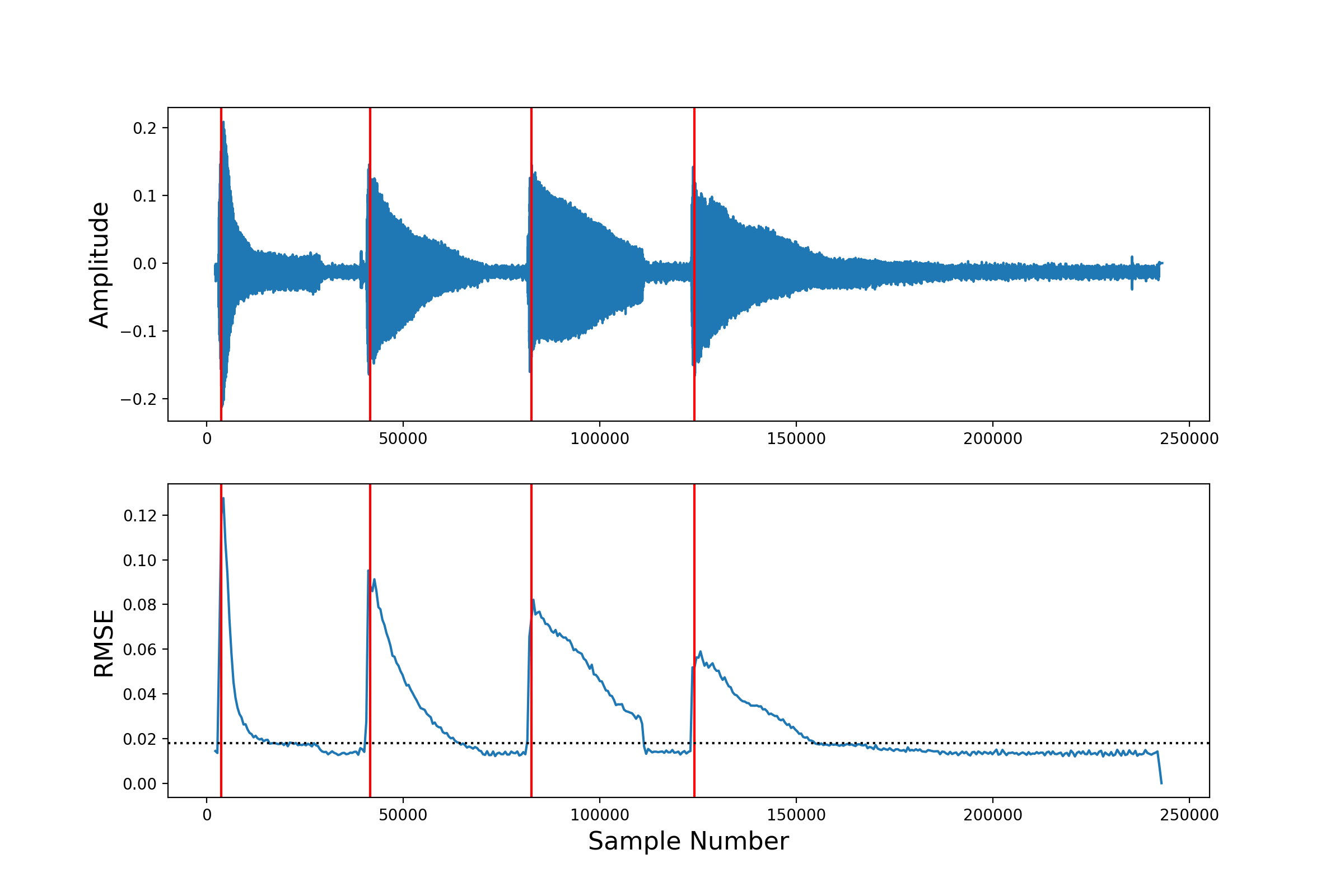
Печатная продукция выглядит так:

In [1]: %run rosatest
[ 0.17124717  1.88952381  3.74712018  5.62793651]
[   3776.   41664.   82624.  124096.]

и сюжет, который он производит, показан ниже:

Answer 2

Вы тестировали, чтобы нормализовать образец звука до лечения?

Читая документацию onset_detect, мы видим, что существует множество дополнительных аргументов, вы уже пытались их использовать?

Возможно, один из этих дополнительных аргументов может помочь вам сохранить только хороший (или, по крайней мере, ограничить размер возвращаемого массива времени начала):

• librosa.util.peak_pick (возможно, лучший)
• отступаться
• энергия

Пожалуйста, смотрите также обновление вашего кода, чтобы использовать предварительно вычисленный конверт:

def detect_pitch(y, sr, onset_offset=5, fmin=75, fmax=1400):
  y = highpass_filter(y, sr)

  o_env = librosa.onset.onset_strength(y, sr=sr)
  times = librosa.frames_to_time(np.arange(len(o_env)), sr=sr)

  onset_frames = librosa.onset.onset_detect(y=o_env, sr=sr)
  pitches, magnitudes = librosa.piptrack(y=y, sr=sr, fmin=fmin, fmax=fmax)

  notes = []

  for i in range(0, len(onset_frames)):
    onset = onset_frames[i] + onset_offset
    index = magnitudes[:, onset].argmax()
    pitch = pitches[index, onset]
    if (pitch != 0):
      notes.append(librosa.hz_to_note(pitch))

  return notes

def highpass_filter(y, sr):
  filter_stop_freq = 70  # Hz
  filter_pass_freq = 100  # Hz
  filter_order = 1001

  # High-pass filter
  nyquist_rate = sr / 2.
  desired = (0, 0, 1, 1)
  bands = (0, filter_stop_freq, filter_pass_freq, nyquist_rate)
  filter_coefs = signal.firls(filter_order, bands, desired, nyq=nyquist_rate)

  # Apply high-pass filter
  filtered_audio = signal.filtfilt(filter_coefs, [1], y)
  return filtered_audio

это работает лучше?