Условия выигрыша в Tic Tac Toe меняются, когда масштабируемая доска больше 4x4

Question

Итак, я делаю эту программу Tic Tac Toe некоторое время. Это базовая игра Tic Tac Toe, но игровое поле является масштабируемым. Программа почти закончена, но одна маленькая функция отсутствует.

Я должен закончить игру, если игрок получает пять или более меток подряд, когда игровое поле больше 4х4.

FE Если игровое поле 9x9, игра должна закончиться, когда игрок или компьютер получат пять отметок подряд.

(Марк = "О" или "Х").

Теперь игра заканчивается, когда кто-то получает метки подряд, равные размеру доски (если 9x9, то для победы нужно 9 меток подряд).

Я должен реализовать функцию в playerHasWon и мне было очень трудно выяснить как. Я думаю, что это просто реализовать, но я не нашел, как это сделать.

Надеюсь, мое объяснение достаточно легко для понимания. Вот код:

package tictac; 

import java.util.Scanner;
import java.util.Random;

public class Tictac {

public static final int DRAW = 0; // game ends as a draw
public static final int COMPUTER = 1; // computer wins
public static final int PLAYER = 2; // player wins
public static final char PLAYER_MARK = 'X'; // The "X"
public static final char COMPUTER_MARK = 'O'; // The "O"

public static int size; // size of the board
public static String[][] board; // the board itself
public static int score = 0; // game win score
public static Scanner scan = new Scanner(System.in); // scanner

/**
 * Builds the board with the integer size and user input.
 * 
 * Displays game win message and switches play turns.
 * 
 * @param args the command line parameters. Not used.
 */
public static void main(String[] args) {

    while (true) {
        System.out.println("Select board size");
        System.out.print("[int]: ");
        try {
            size = Integer.parseInt(scan.nextLine());
        } catch (Exception e) {
            System.out.println("You can't do that.");
            continue; // after message, give player new try
        }

        break;
    }

    int[] move = {};
    board = new String[size][size];
    setupBoard();

    int i = 1;

    loop: // creates the loop

    while (true) {
        if (i % 2 == 1) {
            displayBoard();
            move = getMove();
        } else {
            computerTurn();
        }

        switch (isGameFinished(move)) {
            case PLAYER:
                System.err.println("YOU WIN!");
                displayBoard();
                break loop;
            case COMPUTER:
                System.err.println("COMPUTER WINS!");
                displayBoard();
                break loop;
            case DRAW:
                System.err.println("IT'S A DRAW");
                displayBoard();
                break loop;
        }

        i++;
    }
}

/**
 * Checks for game finish.
 *
 * @param args command line parameters. Not used.
 * 
 * @return DRAW the game ends as draw.
 * @return COMPUTER the game ends as computer win.
 * @return PLAYERE the game ends as player win.
 */
private static int isGameFinished(int[] move) {
    if (isDraw()) {
        return DRAW;
    } else if (playerHasWon(board, move,
            Character.toString(COMPUTER_MARK))) {
        return COMPUTER;
    } else if (playerHasWon(board, move,
            Character.toString(PLAYER_MARK))) {
        return PLAYER;
    }

    return -1; // can't be 0 || 1 || 2
}

/**
 * Checks for win for every direction on the board.
 *
 * @param board the game board.
 * @param move move on the board.
 * @param playerMark mark on the board "X" or "O".
 * @return the game is won.
 */
public static boolean playerHasWon(String[][] board, int[] move,
        String playerMark) { //playermark x || o

    // horizontal check
    for (int i = 0; i < size; i++) {
        if (board[i][0].equals(playerMark)) {
            int j;

            for (j = 1; j < size; j++) {
                if (!board[i][j].equals(playerMark)) {
                    break;
                }
            }

            if (j == size) {
                return true;
            }
        }
    }

    // vertical check
    for (int i = 0; i < size; i++) {
        if (board[0][i].equals(playerMark)) {
            int j;

            for (j = 1; j < size; j++) {
                if (!board[j][i].equals(playerMark)) {
                    break;
                }
            }

            if (j == size) {
                return true;
            }
        }
    }

    // diagonals check
    int i;

    for (i = 0; i < size; i++) {
        if (!board[i][i].equals(playerMark)) {
            break;
        }
    }

    if (i == size) {
        return true;
    }

    for (i = 0; i < size; i++) {
        if (!board[i][(size - 1) - i].equals(playerMark)) {
            break;
        }
    }

    return i == size;
}

/**
 * Checks for draws.
 *
 * @return if this game is a draw.
 */
public static boolean isDraw() {
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            if (board[i][j] == " ") {
                return false;
            }
        }
    }

    return true;
}

/**
 * Displays the board.
 *
 *
 */
public static void displayBoard() {
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            System.out.printf("[%s]", board[i][j]);
        }

        System.out.println();
    }
}

/**
 * Displays the board.
 *
 *
 */
public static void setupBoard() {
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            board[i][j] = " ";
        }
    }
}

/**
 * Takes in user input and sends it to isValidPlay. 
 *
 * @return null.
 */
public static int[] getMove() {

    Scanner sc = new Scanner(System.in);
    System.out.println("Your turn:");

    while (true) {
        try {
            System.out.printf("ROW: [0-%d]: ", size - 1);
            int x = Integer.parseInt(sc.nextLine());
            System.out.printf("COL: [0-%d]: ", size - 1);
            int y = Integer.parseInt(sc.nextLine());

            if (isValidPlay(x, y)) {
                board[x][y] = "" + PLAYER_MARK;
                return new int[]{x, y};
            } else { // if input is unallowed
                System.out.println("You can't do that");
                continue; // after message, give player new try
            }
        } catch (Exception e) {
            System.out.println("You can't do that.");
        }

        return null;
    }
}

/*
 * Randomizes computer's turn, where it inputs the mark 'O'.
 *
 *
 */
public static void computerTurn() {
    Random rgen = new Random();  // Random number generator   

    while (true) {
        int x = (int) (Math.random() * size);
        int y = (int) (Math.random() * size);

        if (isValidPlay(x, y)) {
            board[x][y] = "" + COMPUTER_MARK;
            break;
        }
    }
}

/**
 * Checks if a move is possible.
 *
 * @param inX x-move is out of bounds.
 * @param inY y-move is out of bounds.
 * @return false
 */
public static boolean isValidPlay(int inX, int inY) {

    // Play is out of bounds and thus not valid.
    if ((inX >= size) || (inY >= size)) {
        return false;
    }

    // Checks if a play have already been made at the location,
    // and the location is thus invalid. 
    return (board[inX][inY] == " ");
    }
}

// End of file

Answer 1

Во-первых, я думаю playerMark должен быть char и не String, Тем не менее, давайте идти за ответом. "Горизонтальный" случай будет:

// This is the number of marks in a row required to win
// Adjust formula if necessary
final int required = size > 4 ? 5 : 3;

for (int i = 0; i < size; i++) {
        int currentScore = 0;

        for (j = 0; j < size; j++) {
            if (board[i][j].equals(playerMark)) {
                currentScore++;

                if (currentScore >= required)
                    return true;
            }
            else {
                currentScore = 0;
            }
        }
    }
}

Вертикальный случай будет аналогичным. Диагональ немного сложнее, так как теперь это потребует board[i][i+k] для главной диагонали и board[i][k-i] для среднего; и не может быть очевидно, какие значения k а также i должен пройти. Вот моя попытка (переменная required как в горизонтальном случае):

Примечание: все отсюда было полностью переписано 2015-12-16. Предыдущие версии не работали, и алгоритм не был объяснен.

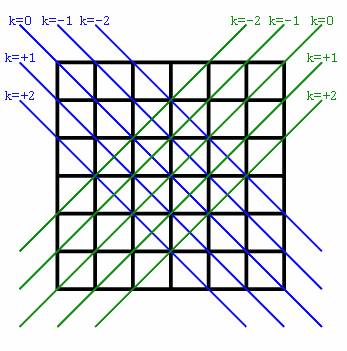
После двух неудачных попыток я решил сделать свою домашнюю работу и на самом деле разобраться, вместо того чтобы делать все, что у меня в голове, думая, что могу отслеживать все переменные. В результате получается эта картина:

Основные диагонали окрашены в синий, вторичные диагонали в зеленый. Каждая диагональ определяется значением k, с k=0 быть всегда самой длинной диагональю каждого набора. Значения k растут по мере того, как диагонали опускаются, поэтому диагонали над самой длинной имеют отрицательный k в то время как диагонали ниже самого длинного имеют положительный k,

Вещи, которые имеют место для обеих диагоналей:

• Диагональ содержит size-abs(k) элементы. Диагонали в которых size-abs(k) меньше чем required не нужно искать. Это означает, что для размера платы size и требуемая длина requiredмы будем искать значения k от required-size в size-required, Обратите внимание, что они имеют одинаковое абсолютное значение с первым <=0 а второй >=0, Эти значения равны нулю только тогда, когда required==sizeт.е. когда нам нужна полная диагональ, чтобы претендовать на победу, т.е. когда нам нужно только искать k=0,
• За k<=0, возможные значения i (строка) идти от 0 в size+k, Значения больше или равны size+k пересечь правый край доски и, таким образом, за пределами доски.
• За k>=0, возможные значения i (строка) идти от k в size, Значения ниже k пересечь левый край доски и, таким образом, за пределами доски.

Только для основных (синих) диагоналей:

• Ценность j (столбец) k+i,

Только для вторичных (зеленых) диагоналей:

• Ценность j (столбец) size-1+k-i, В случае, если это не очевидно, просто выберите верхний правый угол (k=0,i=0) и обратите внимание j=size-1, Затем обратите внимание, что добавление 1 в k (хранение i постоянный) всегда движется j от 1 правильно (это будет выходить из доски, если сделано из k=0,i=0Подумайте только о пересечении горизонтальной линии i=0 с диагональю k=1) и добавление 1 в i (хранение k постоянный) всегда движется j от 1 налево.

Результирующий код будет:// Главная диагональ

for (int k = required - size; k < size - required; k++)
{
    int currentScore = 0;

    startI = Math.max (0, k);
    endI = Math.min (size, size+k);

    for (int i = startI, i < endI; i++)
    {
        if (board[i][k+i].equals (playerMark))
        {
            currentScore++;

            if (currentScore >= required)
                return true;
        }
        else
            currentScore = 0;
    }
}

// Secondary diagonal
for (int k = required - size; k < size - required; k++)
{
    int currentScore = 0;

    startI = Math.max (0, k);
    endI = Math.min (size, size+k);

    for (int i = startI, i < endI; i++)
    {
        if (board[i][size-1+k-i].equals (playerMark))
        {
            currentScore++;

            if (currentScore >= required)
                return true;
        }
        else
            currentScore = 0;
    }
}

На данный момент код почти идентичен в обоих случаях, изменяя только j индекс в board[i][j], Фактически обе петли можно объединить, заботясь только о сохранении двух currentScore переменные, одна для главной (синей) диагонали и другая для вторичной (зеленой) диагонали.

Answer 2

Быстро посмотрел, обнаружил проблему и нашел быстрое решение:

public static boolean checkDiagonal(String markToLook) {
// how many marks are we looking for in row?
int sizeToWin = Math.min(size, 5);

// running down and right
// don't need to iterate rows that can't be the starting point
// of a winning diagonal formation, thus can exlude some with
// row < (size - (sizeToWin - 1))
for (int row = 0; row < (size - (sizeToWin - 1)); row++) {
    for (int col = 0; col < size; col++) {
        int countOfMarks = 0;

        // down and right
        for (int i = row; i < size; i++) {
            if (board[i][i] == null ? markToLook == null :
                    board[i][i].equals(markToLook)) {
                countOfMarks++;

                if (countOfMarks >= sizeToWin) {
                    return true;
                }
            }
        }

        countOfMarks = 0;

        // down and left
        for (int i = row; i < size; i++) {
            if (board[i][size - 1 - i] == null ? markToLook == null :
                    board[i][size - 1 - i].equals(markToLook)) {
                countOfMarks++;

                if (countOfMarks >= sizeToWin) {
                    return true;
                }
            }
        }
    }
}

return false;
}

И вызовите его из вашего метода PlayerHasWon вместо выполнения там проверок. В основном мы перебираем каждый возможный начальный квадрат на доске для диагонального выигрышного формирования, и запускаем проверку вниз + влево и вниз + вправо для каждого из квадратов.

Я ужасно тороплюсь и не слишком много тестирую, но через пару часов вернусь, чтобы улучшить это решение. Кажется, работает.

Изменить: мое предыдущее решение, которое я обнаружил, не хватает в дальнейших тестах, я обновил приведенный выше код, чтобы функционировать по желанию.