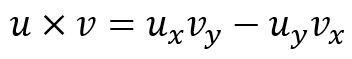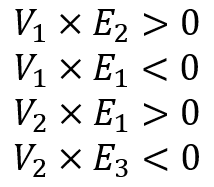Проверка положения мыши в треугольнике - Python

Question

** Это часть курса программирования, и модули, которые нас просят использовать, обычно не используются. Я сделаю все возможное, чтобы объяснить мой код (хотя это довольно очевидно)

РЕДАКТИРОВАТЬ: Если вам интересно, я должен использовать Myro, и код, который я использую, чтобы получить координаты щелчка мыши: mouseX, mouseY = win.getMouse() # "win" refers to a Window object

Я создаю "кнопки", которые при нажатии выполняют какую-то форму действия. У меня есть три разные формы, которые я использую: прямоугольники, круги и треугольники.

Для прямоугольника:

# The numbers used in this example are the coordinates on an XY plane
# mouseX refers to the X coord of a recent mouse click; mouseY on the Y axis
if mouseX >= 70 and mouseX <= 120:
        if mouseY >= 10 and mouseY <= 35:
            print("rectangle button clicked")

Для круга я получил помощь по этому вопросу и получил следующий код:

# mouseX and mouseY, same as rectangle example
if sqrt((mouseX-660)**2 + (mouseY-270)**2) <= 30:
        print("circle button clicked")

Последняя фигура, с которой я пытаюсь работать, это треугольник. Я не уверен, как бы я хотел обеспечить mouseX а также mouseY находятся в пределах координат для формы. Я довольно ужасен в математике, но я предполагаю, что есть некоторая формула, которую можно использовать (например, пример круга). Большое спасибо.

Answer 1

Я нашел ответ как часть этого вопроса, написанного на C (я верю). Я переписал код на Python и оставлю его здесь для других.

Код:

def sign(p1, p2, p3): #all Points
    return (p1.getX() - p3.getX()) * (p2.getY() - p3.getY()) - (p2.getX() - p3.getX()) * (p1.getY() - p3.getY())

def inTriangle(pt, v1, v2, v3): #all Points, pt = mouse, v = triangle vertex
    b1 = sign(pt, v1, v2) < 0.0
    b2 = sign(pt, v2, v3) < 0.0
    b3 = sign(pt, v3, v1) < 0.0
    return ((b1 == b2) and (b2 == b3))

Тестирование:

mouseX, mouseY = win.getMouse() #Myro module, win = Window object
a = Point(662,200)
b = Point(1,1)
print(inTriangle(a, Point(661,156), Point(633,217), Point(688,218))) #TRUE!
print(inTriangle(b, Point(661,156), Point(633,217), Point(688,218))) #FALSE!
triangle = [Point(661, 156), Point(633, 217), Point(688, 218)]
if inTriangle(Point(mouseX, mouseY), triangle[0], triangle[1], triangle[2]):
    print("clicked up")

Answer 2

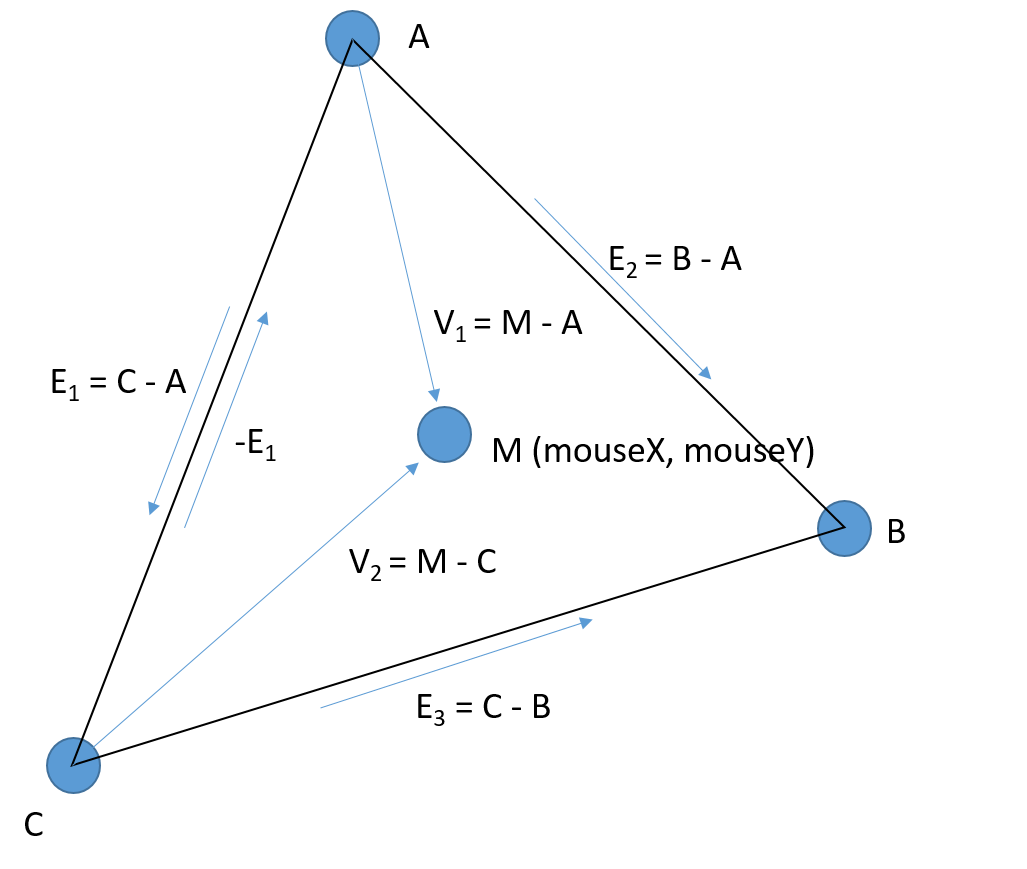
Определите координаты вашего треугольника и мыши следующим образом:

И определить 2D-перекрестное произведение двух векторов u а также v:

Это положительно, если вектор u лежит справа vи отрицательный, если слева.

Итак, четыре условия, которые вы ищете:

... для удара мыши.

(Доступен альтернативный метод с использованием точечного произведения, но он использует квадратные корни, которые довольно неэффективны)

Извиняюсь за отсутствие кода - я ненавижу Python (да, я это сказал). Но это должно обеспечить математику, необходимую для ее реализации.

Answer 3

Использование перекрестных продуктов - все должно быть положительным или отрицательным.

def line_point_pos(start, end, point):
    """right: negative, left: positive, onedge: zero"""
    A = end[0]-start[0], end[1]-start[1]
    B = point[0]-start[0], point[1]-start[1]
    # return z-component of cross product
    return A[0]*B[1] - A[1]*B[0]

def in_polygon(vertices, point, onedges=True):
    """find out if the point is inside the polygon"""
    edges = zip(vertices, vertices[1:] + [vertices[0]])

    zs = [line_point_pos(s, e, point) for s,e in edges]
    if 0 in zs:
        return onedges
    return all(z>0 for z in zs) or all(z<0 for z in zs)

triangle = [(1, 1), (10, 1), (5, 10)]
a = 5, 10
print(in_polygon(triangle, a))      # True