Быстрый расчет Exp: возможно ли повысить точность без потери производительности?
Я пробую быструю функцию Exp(x), которая ранее была описана в этом ответе на вопрос SO об улучшении скорости вычислений в C#:
public static double Exp(double x)
{
var tmp = (long)(1512775 * x + 1072632447);
return BitConverter.Int64BitsToDouble(tmp << 32);
}
Выражение использует некоторые "хитрости" IEEE с плавающей запятой и в первую очередь предназначено для использования в нейронных множествах. Функция примерно в 5 раз быстрее обычной Math.Exp(x) функция.
К сожалению, числовая точность составляет всего -4% - +2% относительно обычной Math.Exp(x) функции, в идеале, я хотел бы иметь точность в пределах как минимум подпроцентного диапазона.
Я составил график между приближенной и регулярной функциями Exp, и, как видно на графике, относительная разница, по-видимому, повторяется практически с постоянной частотой.
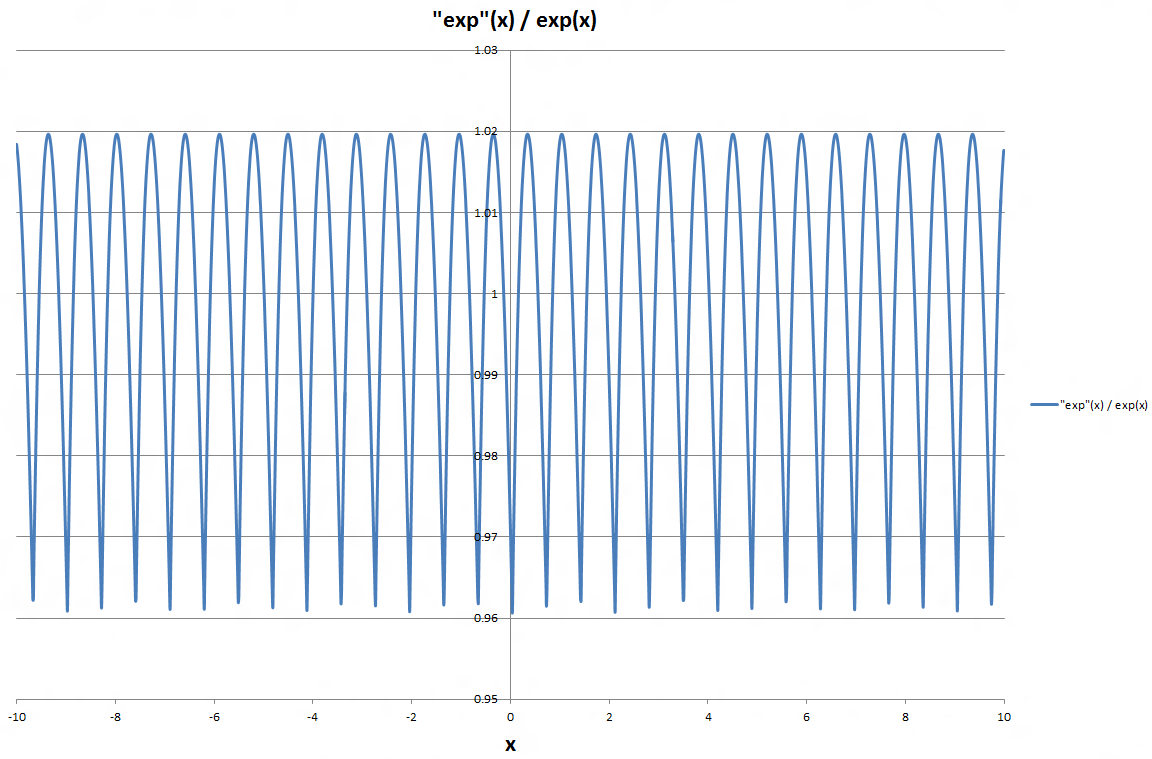
Можно ли воспользоваться этой регулярностью для дальнейшего повышения точности функции "быстрого опыта" без существенного снижения скорости вычислений, или перерасход вычислительных затрат на повышение точности перевесит вычислительный выигрыш исходного выражения?
(В качестве примечания я также попробовал один из альтернативных подходов, предложенных в том же вопросе SO, но этот подход не представляется вычислительно эффективным в C#, по крайней мере, не для общего случая.)
ОБНОВЛЕНИЕ 14 МАЯ
По запросу @Adriano я выполнил очень простой тест. Я выполнил 10 миллионов вычислений, используя каждую из альтернативных функций exp для значений с плавающей запятой в диапазоне [-100, 100]. Поскольку диапазон значений, которые меня интересуют, составляет от -20 до 0, я также явно указал значение функции при x = -5. Вот результаты:
Math.Exp: 62.525 ms, exp(-5) = 0.00673794699908547
Empty function: 13.769 ms
ExpNeural: 14.867 ms, exp(-5) = 0.00675211846828461
ExpSeries8: 15.121 ms, exp(-5) = 0.00641270968867667
ExpSeries16: 32.046 ms, exp(-5) = 0.00673666189488182
exp1: 15.062 ms, exp(-5) = -12.3333325982094
exp2: 15.090 ms, exp(-5) = 13.708332516253
exp3: 16.251 ms, exp(-5) = -12.3333325982094
exp4: 17.924 ms, exp(-5) = 728.368055056781
exp5: 20.972 ms, exp(-5) = -6.13293614238501
exp6: 24.212 ms, exp(-5) = 3.55518353166184
exp7: 29.092 ms, exp(-5) = -1.8271053775984
exp7 +/-: 38.482 ms, exp(-5) = 0.00695945286970704
ExpNeural эквивалентен функции Exp, указанной в начале этого текста. ExpSeries8 - формулировка, которую я изначально утверждал, что она не очень эффективна в.NET; когда он реализован так же, как Нил, все было очень быстро. ExpSeries16 - аналогичная формула, но с 16 умножениями вместо 8. exp1 - exp7 - это разные функции из ответа Адриано ниже. Последний вариант exp7 - это вариант, где проверяется знак x; если отрицательный, функция возвращает 1/exp(-x) вместо.
К сожалению, ни одна из функций expN, перечисленных Адриано, не является достаточной в более широком диапазоне отрицательных значений, который я рассматриваю. Подход последовательного расширения Нейлом Коффи кажется более подходящим в диапазоне значений "my", хотя он слишком быстро расходится с большим отрицательным x, особенно при использовании "только" 8 умножений.
7 ответов
В случае, если кто-то хочет повторить функцию относительной ошибки, показанную в вопросе, вот способ использования Matlab ("быстрый" показатель не очень быстрый в Matlab, но он точный):
t = 1072632447+[0:ceil(1512775*pi)];
x = (t - 1072632447)/1512775;
ex = exp(x);
t = uint64(t);
import java.lang.Double;
et = arrayfun( @(n) java.lang.Double.longBitsToDouble(bitshift(n,32)), t );
plot(x, et./ex);
Теперь период ошибки точно совпадает с тем, когда двоичное значение tmp перетекает из мантиссы в экспоненту. Давайте разберем наши данные на бункеры, отбросив биты, которые становятся экспонентой (делая их периодическими), и оставив только оставшиеся восемь старших битов (чтобы сделать нашу справочную таблицу разумным размером):
index = bitshift(bitand(t,uint64(2^20-2^12)),-12) + 1;
Теперь рассчитаем среднее значение требуемой корректировки:
relerrfix = ex./et;
adjust = NaN(1,256);
for i=1:256; adjust(i) = mean(relerrfix(index == i)); end;
et2 = et .* adjust(index);
Относительная ошибка уменьшена до +/- .0006. Конечно, возможны и другие размеры таблиц (например, 6-битная таблица с 64 записями дает +/- .0025), и ошибка является почти линейной по размеру таблицы. Линейная интерполяция между записями таблицы еще больше улучшит ошибку, но за счет производительности. Так как мы уже достигли цели точности, давайте избегать дальнейших падений производительности.
На данный момент это несколько тривиальных навыков редактора, чтобы взять значения, вычисленные MatLab, и создать таблицу поиска в C#. Для каждого вычисления мы добавляем битовую маску, поиск в таблице и умножение с двойной точностью.
static double FastExp(double x)
{
var tmp = (long)(1512775 * x + 1072632447);
int index = (int)(tmp >> 12) & 0xFF;
return BitConverter.Int64BitsToDouble(tmp << 32) * ExpAdjustment[index];
}
Ускорение очень похоже на исходный код - для моего компьютера это примерно на 30% быстрее скомпилировано как x86 и примерно в 3 раза быстрее для x64. С моно на ideone это существенный чистый убыток (но так же, как и оригинал).
Полный исходный код и контрольный пример: http://ideone.com/UwNgx
using System;
using System.Diagnostics;
namespace fastexponent
{
class Program
{
static double[] ExpAdjustment = new double[256] {
1.040389835,
1.039159306,
1.037945888,
1.036749401,
1.035569671,
1.034406528,
1.033259801,
1.032129324,
1.031014933,
1.029916467,
1.028833767,
1.027766676,
1.02671504,
1.025678708,
1.02465753,
1.023651359,
1.022660049,
1.021683458,
1.020721446,
1.019773873,
1.018840604,
1.017921503,
1.017016438,
1.016125279,
1.015247897,
1.014384165,
1.013533958,
1.012697153,
1.011873629,
1.011063266,
1.010265947,
1.009481555,
1.008709975,
1.007951096,
1.007204805,
1.006470993,
1.005749552,
1.005040376,
1.004343358,
1.003658397,
1.002985389,
1.002324233,
1.001674831,
1.001037085,
1.000410897,
0.999796173,
0.999192819,
0.998600742,
0.998019851,
0.997450055,
0.996891266,
0.996343396,
0.995806358,
0.995280068,
0.99476444,
0.994259393,
0.993764844,
0.993280711,
0.992806917,
0.992343381,
0.991890026,
0.991446776,
0.991013555,
0.990590289,
0.990176903,
0.989773325,
0.989379484,
0.988995309,
0.988620729,
0.988255677,
0.987900083,
0.987553882,
0.987217006,
0.98688939,
0.98657097,
0.986261682,
0.985961463,
0.985670251,
0.985387985,
0.985114604,
0.984850048,
0.984594259,
0.984347178,
0.984108748,
0.983878911,
0.983657613,
0.983444797,
0.983240409,
0.983044394,
0.982856701,
0.982677276,
0.982506066,
0.982343022,
0.982188091,
0.982041225,
0.981902373,
0.981771487,
0.981648519,
0.981533421,
0.981426146,
0.981326648,
0.98123488,
0.981150798,
0.981074356,
0.981005511,
0.980944219,
0.980890437,
0.980844122,
0.980805232,
0.980773726,
0.980749562,
0.9807327,
0.9807231,
0.980720722,
0.980725528,
0.980737478,
0.980756534,
0.98078266,
0.980815817,
0.980855968,
0.980903079,
0.980955475,
0.981017942,
0.981085714,
0.981160303,
0.981241675,
0.981329796,
0.981424634,
0.981526154,
0.981634325,
0.981749114,
0.981870489,
0.981998419,
0.982132873,
0.98227382,
0.982421229,
0.982575072,
0.982735318,
0.982901937,
0.983074902,
0.983254183,
0.983439752,
0.983631582,
0.983829644,
0.984033912,
0.984244358,
0.984460956,
0.984683681,
0.984912505,
0.985147403,
0.985388349,
0.98563532,
0.98588829,
0.986147234,
0.986412128,
0.986682949,
0.986959673,
0.987242277,
0.987530737,
0.987825031,
0.988125136,
0.98843103,
0.988742691,
0.989060098,
0.989383229,
0.989712063,
0.990046579,
0.990386756,
0.990732574,
0.991084012,
0.991441052,
0.991803672,
0.992171854,
0.992545578,
0.992924825,
0.993309578,
0.993699816,
0.994095522,
0.994496677,
0.994903265,
0.995315266,
0.995732665,
0.996155442,
0.996583582,
0.997017068,
0.997455883,
0.99790001,
0.998349434,
0.998804138,
0.999264107,
0.999729325,
1.000199776,
1.000675446,
1.001156319,
1.001642381,
1.002133617,
1.002630011,
1.003131551,
1.003638222,
1.00415001,
1.004666901,
1.005188881,
1.005715938,
1.006248058,
1.006785227,
1.007327434,
1.007874665,
1.008426907,
1.008984149,
1.009546377,
1.010113581,
1.010685747,
1.011262865,
1.011844922,
1.012431907,
1.013023808,
1.013620615,
1.014222317,
1.014828902,
1.01544036,
1.016056681,
1.016677853,
1.017303866,
1.017934711,
1.018570378,
1.019210855,
1.019856135,
1.020506206,
1.02116106,
1.021820687,
1.022485078,
1.023154224,
1.023828116,
1.024506745,
1.025190103,
1.02587818,
1.026570969,
1.027268461,
1.027970647,
1.02867752,
1.029389072,
1.030114973,
1.030826088,
1.03155163,
1.032281819,
1.03301665,
1.033756114,
1.034500204,
1.035248913,
1.036002235,
1.036760162,
1.037522688,
1.038289806,
1.039061509,
1.039837792,
1.040618648
};
static double FastExp(double x)
{
var tmp = (long)(1512775 * x + 1072632447);
int index = (int)(tmp >> 12) & 0xFF;
return BitConverter.Int64BitsToDouble(tmp << 32) * ExpAdjustment[index];
}
static void Main(string[] args)
{
double[] x = new double[1000000];
double[] ex = new double[x.Length];
double[] fx = new double[x.Length];
Random r = new Random();
for (int i = 0; i < x.Length; ++i)
x[i] = r.NextDouble() * 40;
Stopwatch sw = new Stopwatch();
sw.Start();
for (int j = 0; j < x.Length; ++j)
ex[j] = Math.Exp(x[j]);
sw.Stop();
double builtin = sw.Elapsed.TotalMilliseconds;
sw.Reset();
sw.Start();
for (int k = 0; k < x.Length; ++k)
fx[k] = FastExp(x[k]);
sw.Stop();
double custom = sw.Elapsed.TotalMilliseconds;
double min = 1, max = 1;
for (int m = 0; m < x.Length; ++m) {
double ratio = fx[m] / ex[m];
if (min > ratio) min = ratio;
if (max < ratio) max = ratio;
}
Console.WriteLine("minimum ratio = " + min.ToString() + ", maximum ratio = " + max.ToString() + ", speedup = " + (builtin / custom).ToString());
}
}
}
Приближения ряда Тейлора (такие как expX() функции в ответе Адриано) наиболее точны вблизи нуля и могут иметь огромные ошибки при -20 или даже -5. Если вход имеет известный диапазон, например, от -20 до 0, как в исходном вопросе, вы можете использовать небольшую справочную таблицу и одно дополнительное умножение, чтобы значительно повысить точность.
Хитрость заключается в том, чтобы распознать, что exp() можно разделить на целые и дробные части. Например:
exp(-2.345) = exp(-2.0) * exp(-0.345)
Дробная часть всегда будет между -1 и 1, поэтому приближение ряда Тейлора будет довольно точным. Целочисленная часть имеет только 21 возможное значение от exp(-20) до exp(0), поэтому они могут быть сохранены в небольшой справочной таблице.
Попробуйте следующие варианты (exp1 быстрее, exp7 точнее).
Код
public static double exp1(double x) {
return (6+x*(6+x*(3+x)))*0.16666666f;
}
public static double exp2(double x) {
return (24+x*(24+x*(12+x*(4+x))))*0.041666666f;
}
public static double exp3(double x) {
return (120+x*(120+x*(60+x*(20+x*(5+x)))))*0.0083333333f;
}
public static double exp4(double x) {
return 720+x*(720+x*(360+x*(120+x*(30+x*(6+x))))))*0.0013888888f;
}
public static double exp5(double x) {
return (5040+x*(5040+x*(2520+x*(840+x*(210+x*(42+x*(7+x)))))))*0.00019841269f;
}
public static double exp6(double x) {
return (40320+x*(40320+x*(20160+x*(6720+x*(1680+x*(336+x*(56+x*(8+x))))))))*2.4801587301e-5;
}
public static double exp7(double x) {
return (362880+x*(362880+x*(181440+x*(60480+x*(15120+x*(3024+x*(504+x*(72+x*(9+x)))))))))*2.75573192e-6;
}
точность
Ошибка функции в [-1...1] Ошибка в [3.14...3.14] exp1 0,05 1,8% 8,8742 38,40% exp2 0,01 0,36% 4,8237 20,80% exp3 0,0016152 0,59% 2,28 9,80% exp4 0,0002263 0,0083% 0,9488 4,10% exp5 0,0000279 0,001% 0,3516 1,50% exp6 0,0000031 0,00011% 0,1172 0,50% exp7 0,0000003 0,000011% 0,0355 0,15%
кредиты
Эти реализации exp() были рассчитаны "scoofy" с использованием ряда Тейлора из tanh() реализация "fuzzpilz" (кем бы они ни были, у меня просто были эти ссылки в моем коде).
Следующий код должен соответствовать требованиям к точности, так как для входных данных в [-87,88] результаты имеют относительную погрешность <= 1,73e-3. Я не знаю C#, так что это код на C, но преобразование должно быть неудачным.
Я предполагаю, что, поскольку требование к точности низкое, использование вычислений с одинарной точностью вполне допустимо. Используется классический алгоритм, в котором вычисление exp() отображается на вычисление exp2(). После преобразования аргумента с помощью умножения на log2(e) возведение в степень дробной части обрабатывается с использованием минимаксного полинома степени 2, тогда как возведение в степень интегральной частью аргумента выполняется путем прямого манипулирования экспоненциальной частью одного IEEE-754 -точный номер.
Изменчивое объединение облегчает повторную интерпретацию битового шаблона как целое число или число с плавающей запятой одинарной точности, необходимое для манипулирования экспонентой. Похоже, что C# предлагает для этого определенные функции повторной интерпретации, что намного чище.
Двумя потенциальными проблемами производительности являются функция floor() и преобразование float->int. Традиционно оба были медленными на x86 из-за необходимости обрабатывать динамическое состояние процессора. Но SSE (в частности, SSE 4.1) предоставляет инструкции, которые позволяют выполнять эти операции быстро. Я не знаю, может ли C# использовать эти инструкции.
/* max. rel. error <= 1.73e-3 on [-87,88] */
float fast_exp (float x)
{
volatile union {
float f;
unsigned int i;
} cvt;
/* exp(x) = 2^i * 2^f; i = floor (log2(e) * x), 0 <= f <= 1 */
float t = x * 1.442695041f;
float fi = floorf (t);
float f = t - fi;
int i = (int)fi;
cvt.f = (0.3371894346f * f + 0.657636276f) * f + 1.00172476f; /* compute 2^f */
cvt.i += (i << 23); /* scale by 2^i */
return cvt.f;
}
Я изучил статью Никола Шраудольфа, в которой оригинальная реализация C вышеуказанной функции была определена более подробно. Похоже, что, по-видимому, невозможно существенно подтвердить точность вычислений exp без существенного влияния на производительность. С другой стороны, аппроксимация действительна также для больших величин х, вплоть до +/- 700, что, конечно, выгодно.
Реализация функции выше настроена для получения минимальной среднеквадратической ошибки. Шраудольф описывает, как аддитивный член в выражении tmp может быть изменен для достижения альтернативных свойств аппроксимации.
"exp" >= exp for all x 1072693248 - (-1) = 1072693249
"exp" <= exp for all x - 90253 = 1072602995
"exp" symmetric around exp - 45799 = 1072647449
Mimimum possible mean deviation - 68243 = 1072625005
Minimum possible root-mean-square deviation - 60801 = 1072632447
Он также указывает, что на "микроскопическом" уровне приближенная функция "exp" демонстрирует поведение на лестничной основе, поскольку при преобразовании из long в удваивается32 бита. Это означает, что функция является кусочно-постоянной в очень небольшом масштабе, но функция, по крайней мере, никогда не уменьшается с увеличением x.
Для своего рода мета-обзора различных ответов, предложенных выше, я закодировал подпрограммы на C# и проверил ошибку в диапазоне от -87 до +88, увеличивая на 0,1 (за исключением интервала между -10 и +10, где я увеличивал на 0,01). для более высокого разрешения):
- Функция, использующая @Adriano
exp3()для дробной части в сочетании с таблицей поиска целой части числа с плавающей запятой в диапазоне [-88, 88]:- макс |ошибка|: 0,308%
- среднее |ошибка|: 0,009%
- среднее ускорение относительно: 30,86%
- Это было самое низкое среднее значение |error| (не max |error|), но ускорение было не таким уж впечатляющим.
- Ответ @njuffa для float :
- макс |ошибка|: 0,173%
- среднее |ошибка|: 0,108%
- среднее ускорение относительно: 43,52%
- Я реализовал это, используя структуру C# с StructLayout(LayoutKind.Explicit). Этот ответ мог быть на 60% быстрее, чем . К сожалению, подражать
Math.Floor()(что слишком медленно), вам нужно использовать(int)fltусечение; но для отрицательных значений это усечение -1 (поскольку приведение к int приближается к нулю). Я не смог найти быстрый способ имитировать такое поведение. Даже одинifсравнение (flt < 0f), привело к падению производительности примерно с 60% до 43,5% (и я пробовал много разных вариантов — очень жаль).
- @BenVoigt ответ на двойной :
- макс |ошибка|: 0,060%
- среднее |ошибка|: 0,012%
- среднее ускорение относительно (после коррекции границ): 45,97%
- Таблица корректировок Бена значительно уменьшила средние и максимальные ошибки ценой примерно -10% ускорения исходной функции плаката.
- Это решение также страдает от катастрофического переполнения экспоненты на крайних концах диапазона . Поэтому вам нужно сначала проверить границы (см. исправленную функцию внизу этого поста).
- @AndersGustafsson исходная опубликованная функция для double:
- макс |ошибка|: 3,940%
- среднее |ошибка|: 1,520%
- среднее ускорение относительно
Math.Exp()(после коррекции границ): 55,55% - Исходная двухстрочная функция, размещенная вверху, была самой быстрой, которую я нашел, хотя и с самой большой ошибкой.
- Это решение также страдает от катастрофического переполнения экспоненты на крайних концах диапазона.
x. Поэтому вам нужно сначала проверить границы (аналогично исправленной функции внизу этого поста).
Я пришел к выводу, что ответ @BenVoigt (после исправления проверок границ) является победителем, если только вы не можете допустить ошибку в исходной опубликованной функции. Если вы пишете код на C/C++, у вас есть много дополнительных более быстрых вариантов использования встроенных функций SSE, сборки и т. д. ( более подробную информацию см. здесь в ответах SO).
static double FastExp(double x)
{
// must check bounds first!
if (x < -709)
return 0.0;
else if (x > 709)
return double.PositiveInfinity;
var tmp = (long)(1512775 * x + 1072632447);
int index = (int)(tmp >> 12) & 0xFF;
return BitConverter.Int64BitsToDouble(tmp << 32) * ExpAdjustment[index];
}
Я разработал для своих целей следующую функцию, которая быстро и точно вычисляет натуральный показатель с одинарной точностью. Функция работает во всем диапазоне значений float. Код написан под Visual Studio (x86).
_declspec(naked) float _vectorcall fexp(float x)
{
static const float ct[8] = // Constants table
{
1.44269502f, // lb(e)
1.92596299E-8f, // Correction to the value lb(e)
-9.21120925E-4f, // 16*b2
0.115524396f, // 4*b1
2.88539004f, // b0
4.29496730E9f, // 2^32
0.5f, // 0.5
2.32830644E-10f // 2^-32
};
_asm
{
mov ecx,offset ct // ecx contains the address of constants tables
vmulss xmm1,xmm0,[ecx] // xmm1 = x*lb(e)
vcvtss2si eax,xmm1 // eax = round(x*lb(e)) = k
vcvtsi2ss xmm1,xmm1,eax // xmm1 = k
dec eax // of=1, if eax=80000000h, i.e. overflow
jno exp_cont // Jump to form 2^k, if k is normal
vucomiss xmm0,xmm0 // Compare xmm0 with itself to identify NaN
jp exp_end // Complete with NaN result, if x=NaN
vmovd eax,xmm0 // eax contains the bits of x
test eax,eax // sf=1, if x<0; of=0 always
exp_break: // Get 0 for x<0 or Inf for x>0
vxorps xmm0,xmm0,xmm0 // xmm0 = 0
jle exp_end // Ready, if x<<0
vrcpss xmm0,xmm0,xmm0 // xmm0 = Inf at case x>>0
exp_end: // The result at xmm0 is ready
ret // Return
exp_cont: // Continue if |x| is not too big
vfmsub231ss xmm1,xmm0,[ecx] // xmm1 = x*lb(e)-k = t/2 in the range from -0,5 to 0,5
cdq // edx=-1, if x<0, othervice edx=0
vfmadd132ss xmm0,xmm1,[ecx+4] // xmm0 = t/2 (corrected value)
and edx,8 // edx=8, if x<0, othervice edx=0
vmulss xmm2,xmm0,xmm0 // xmm2 = t^2/4 - the argument of polynomial
vmovss xmm1,[ecx+8] // Initialize the sum with highest coefficient 16*b2
lea eax,[eax+8*edx+97] // The exponent of 2^(k-31), if x>0, othervice 2^(k+33)
vfmadd213ss xmm1,xmm2,[ecx+12] // xmm1 = 4*b1+4*b2*t^2
test eax,eax // Test the sign of x
jle exp_break // Result is 0 if the exponent is too small
vfmsub213ss xmm1,xmm2,xmm0 // xmm1 = -t/2+b1*t^2+b2*t^4
cmp eax,254 // Check that the exponent is not too large
ja exp_break // Jump to set Inf if overflow
vaddss xmm1,xmm1,[ecx+16] // xmm1 = b0-t/2+b1*t^2+b2*t^4 = f(t)-t/2
shl eax,23 // eax contains the bits of 2^(k-31) or 2^(k+33)
vdivss xmm0,xmm0,xmm1 // xmm0 = t/(2*f(t)-t)
vmovd xmm2,eax // xmm2 = 2^(k-31), if x>0; otherwice 2^(k+33)
vaddss xmm0,xmm0,[ecx+24] // xmm0 = t/(2*f(t)-t)+0,5
vmulss xmm0,xmm0,xmm2 // xmm0 = e^x with shifted exponent of +-32
vmulss xmm0,xmm0,[ecx+edx+20] // xmm0 = e^x with corrected exponent
ret // Return
}
}