Как конечные автоматы реализованы в коде?
Как реализовать dfa или nfa по этому вопросу в коде Python?
Какие есть хорошие способы сделать это в Python? И используются ли они когда-либо в реальных проектах?
7 ответов
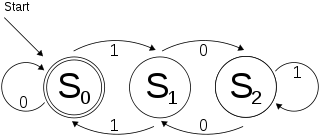
Простой способ представить DFA - это словарь словарей. Для каждого состояния создайте словарь, в котором используются буквы алфавита, а затем глобальный словарь, в котором указаны состояния. Например, следующий DFA из статьи Википедии о DFA
может быть представлен словарь, как это:
dfa = {0:{'0':0, '1':1},
1:{'0':2, '1':0},
2:{'0':1, '1':2}}
"Запустить" dfa для входной строки, взятой из рассматриваемого алфавита (после указания начального состояния и набора принимаемых значений), просто:
def accepts(transitions,initial,accepting,s):
state = initial
for c in s:
state = transitions[state][c]
return state in accepting
Вы начинаете в начальном состоянии, шаг за шагом проходите строку за символом и на каждом шаге просто просматриваете следующее состояние. Когда вы закончите, шагая по строке, вы просто проверяете, находится ли конечное состояние в наборе принимающих состояний.
Например
>>> accepts(dfa,0,{0},'1011101')
True
>>> accepts(dfa,0,{0},'10111011')
False
Для NFA вы можете хранить наборы возможных состояний, а не отдельные состояния в словарях перехода и использовать random модуль для выбора следующего состояния из множества возможных состояний.
Хорошо, здесь я представляю рекурсивное решение для NFA.
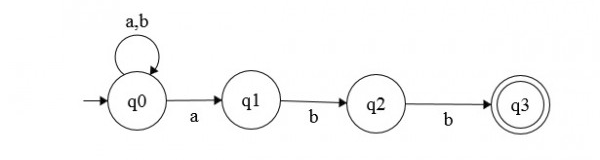
рассмотрим следующее нфа:
переходы могут быть представлены с использованием списка списков следующим образом:
переход = [[[0,1],[0]], [[4],[2]], [[4],[3]], [[4],[4]],[[4],[4]]]
Примечание. Состояние 4 является гипотетическим. Как только вы перейдете в это состояние, вы не сможете двигаться дальше. Это полезно, когда вы не можете прочитать ввод из текущего состояния. Вы непосредственно переходите в состояние 4 и говорите, что ввод данных не принимается для текущего прогресса (проверьте другие возможности, вернувшись назад). например, если вы находитесь в q1и текущий входной символ 'a', вы переходите в состояние 4 и дальше останавливаете вычисления.
вот код Python:
#nfa simulation for (a|b)*abb
#state 4 is a trap state
import sys
def main():
transition = [[[0,1],[0]], [[4],[2]], [[4],[3]], [[4],[4]]]
input = raw_input("enter the string: ")
input = list(input) #copy the input in list because python strings are immutable and thus can't be changed directly
for index in range(len(input)): #parse the string of a,b in 0,1 for simplicity
if input[index]=='a':
input[index]='0'
else:
input[index]='1'
final = "3" #set of final states = {3}
start = 0
i=0 #counter to remember the number of symbols read
trans(transition, input, final, start, i)
print "rejected"
def trans(transition, input, final, state, i):
for j in range (len(input)):
for each in transition[state][int(input[j])]: #check for each possibility
if each < 4: #move further only if you are at non-hypothetical state
state = each
if j == len(input)-1 and (str(state) in final): #last symbol is read and current state lies in the set of final states
print "accepted"
sys.exit()
trans(transition, input[i+1:], final, state, i) #input string for next transition is input[i+1:]
i = i+1 #increment the counter
main()
пример вывода:(строки, заканчивающиеся на abb, принимаются)
enter the string: abb
accepted
enter the string: aaaabbbb
rejected
......
Вот моя версия реализации dfa, если вы ищете более объектно-ориентированную. Однако я был слегка вдохновлен ответом Джона Коулмана.
class Node:
def __init__(self, val):
self.val = val
self.links = []
def add_link(self, link):
self.links.append(link)
def __str__(self):
node = "(%s):\n" % self.val
for link in self.links:
node += "\t" + link + "\n"
return node
def __add__(self, other):
return str(self) + other
def __radd__(self, other):
return other + str(self)
def equals(self, node):
ok = (self.val == node.val)
if len(self.links) == len(node.links):
for i in range(len(self.links)):
ok = ok and (self.links[i] == node.links[i])
return ok
else:
return False
class Link:
def __init__(self, from_node, etiquette, to_node):
self.from_node = from_node
self.etiquette = etiquette
self.to_node = to_node
def __str__(self):
return "(%s --%s--> %s)" % (self.from_node.val, self.etiquette, self.to_node.val)
def __add__(self, other):
return str(self) + other
def __radd__(self, other):
return other + str(self)
def equals(self, link):
return (self.from_node == link.from_node) and (self.etiquette == link.etiquette) and (self.to_node == link.to_node)
class Automata:
def __init__(self, initial_node, nodes, terminal_node):
self.initial_node = initial_node
self.nodes = nodes
self.terminal_node = terminal_node
def get_next_node(self, current_node, etiquette):
for link in current_node.links:
if link.etiquette == etiquette:
return link.to_node
return None
def accepts(self, string):
node = self.initial_node
for character in string:
node = self.get_next_node(node, character)
return self.terminal_node.equals(node)
def __str__(self):
automata = "Initial node: %s\nTerminal node: %s\n" % (self.initial_node.val, self.terminal_node.val)
for node in self.nodes:
automata += node
return automata
def __add__(self, other):
return str(self) + other
def __radd__(self, other):
return other + str(self)
if __name__ == '__main__':
pass
s0 = Node("s0")
s1 = Node("s1")
s2 = Node("s2")
s0_0_s0 = Link(s0, '0', s0)
s0_1_s1 = Link(s0, '1', s1)
s1_0_s2 = Link(s1, '0', s2)
s1_1_s0 = Link(s1, '1', s0)
s2_0_s1 = Link(s2, '0', s1)
s2_1_s2 = Link(s2, '1', s2)
s0.add_link(s0_0_s0)
s0.add_link(s0_1_s1)
s1.add_link(s1_0_s2)
s1.add_link(s1_1_s0)
s2.add_link(s2_0_s1)
s2.add_link(s2_1_s2)
a = Automata(s0, [s0, s1, s2], s0)
print(a)
print(a.accepts('1011101')) #True
print(a.accepts('10111011')) #False
Вам не нужен цикл for over range(len(input)), если вы используете рекурсию. Вы слишком усложняете код. Вот упрощенная версия
import sys
def main():
transition = [[[0,1],[0]], [[4],[2]], [[4],[3]], [[4],[4]]]
input = raw_input("enter the string: ")
input = list(input) #copy the input in list because python strings are immutable and thus can't be changed directly
for index in range(len(input)): #parse the string of a,b in 0,1 for simplicity
if input[index]=='a':
input[index]='0'
else:
input[index]='1'
final = "3" #set of final states = {3}
start = 0
trans(transition, input, final, start)
print "rejected"
def trans(transition, input, final, state):
for each in transition[state][int(input[0])]: #check for each possibility
if each < 4: #move further only if you are at non-hypothetical state
state = each
if len(input)==1:
if (str(state) in final): #last symbol is read and current state lies in the set of final states
print "accepted"
sys.exit()
else:
continue
trans(transition, input[1:], final, state) #input string for next transition is input[i+1:]
main()
Я реализовал DFA, который работает с любым из DFA. Но это не объектно-ориентированный шаблон.
states=list(map(int,input("Enter States : ").split(" ")))
symbols=list(input("Enter Symbols : ").split(" "))
initial_state=int(input("Enter initial state : "))
final_states=list(map(int,input("Enter final states : ").split(" ")))
transitions=[]
inlists=[]
for i in range(len(symbols)):
print("Enter transitions for symbol "+symbols[i]+" from all states :")
for j in range(len(states)):
inlists.append(int(input()))
transitions.append(inlists)
inlists=[]
cur_state=initial_state
while(1):
cur_state=initial_state
string=input("Enter string : ")
if string=='#':
break
for symbol in string:
print("["+str(cur_state)+"]"+"-"+symbol+"->",end="")
cur_state=transitions[symbols.index(symbol)][cur_state]
if cur_state in final_states:
print("["+str(cur_state)+"]")
print("String is accepted.")
else:
print("["+str(cur_state)+"]")
print("String is not accepted.")
Чтобы продемонстрировать мое решение, возьмем в качестве примера следующий DFA:
Язык над 𝛴 = (0, 1), содержащий строки, состоящие только из единиц, или строки, в которых за каждым 0 следует 1.
Таблица переходов для этого DFA:
Моя программа, написанная на Python3, предназначена для приема таблицы переходов любого DFA по алфавиту (0, 1), чтобы проверить, будет ли строка принята DFA или нет.
Чтобы использовать мою программу, мы должны ввести приведенную выше таблицу переходов в следующем формате в текстовый файл с именем fa.txt, находящийся в том же каталоге, что и программа.
fa.txt:
->*s(a,s)
a(d,s)
d(d,d)
Для начального состояния имени состояния должен предшествовать ->, а конечному состоянию должен предшествовать *. В случае, если начальное состояние является конечным, знак -> должен стоять перед *. Название штата должно состоять из одного символа. Начальное состояние должно называться s. Порядок состояний в файле TXT значения не имеет.
Код:
file = open("fa.txt", "r")
l = file.readlines()
x = 0
def findState(state):
lines = l
for i in range(0, len(lines)):
if lines[i][0] == '-':
lines[i] = lines[i][2::]
if lines[i][0] == '*':
if state == lines[i][1]:
return [lines[i][3], lines[i][5], 1]
if lines[i][0] == state:
return [lines[i][2], lines[i][4], 0] # state to go to on 0, state to go to on 1, is it final?
s = input("Enter a binary string to test it against the DFA in file fa.txt: ")
on0_on1 = findState('s') # start state
print("s", end = "")
for c in range(0, len(s)):
if s[c] != '0' and s[c] != '1':
print("Fail")
exit(0)
if s[c] == '0':
print(' ---0--->', on0_on1[0], end = '')
on0_on1 = findState(on0_on1[0])
else:
print(' ---1--->', on0_on1[1], end = '')
on0_on1 = findState(on0_on1[1])
if on0_on1[2] == 1 and c == len(s) - 1:
print("\nPass")
elif c == len(s) - 1 and on0_on1[2] == 0:
print("\nFail")
Принятие строки 101 * и 001 * модификации @John Coleman
#Dfa только для приема 101+00101001
dfa101 = {0:{'1':1},
1:{'0':2},
2:{'1':3},
3:{'0':3, '1':3}}
#Dfa for accepting only 001+00101001
dfa001={0:{'0':1},
1:{'0':2},
2:{'1':3},
3:{'0':3, '1':3}}
def accepts(transitions,initial,accepting,s):
state = initial
try:
for c in s:
state = transitions[state][c]
if(state in accepting):
return 'Accepted'
else:
return 'Rejected'
except:
return 'Rejected'
print('Dfa of 101+ ',accepts(dfa101,0,{3},'10101111000')) #Accepted
print('Dfa of 001+ ',accepts(dfa001,0,{3},'00101010101')) #Accepted