Функция для создания цветовых колес
Это то, что я много раз решал псевдо, и никогда не находил решения.
Проблема состоит в том, чтобы придумать способ генерировать N цвета, которые настолько различимы, насколько это возможно, где N это параметр.
8 ответов
Моя первая мысль об этом: "Как создать N векторов в пространстве, которые максимизируют расстояние друг от друга".
Вы можете видеть, что RGB (или любой другой используемый вами масштаб, который составляет основу в цветовом пространстве) - это просто векторы. Взгляните на случайный выбор точки. Как только у вас есть набор векторов, которые максимизируются друг от друга, вы можете сохранить их в хеш-таблице или что-то на потом, и просто выполнить случайные повороты над ними, чтобы получить все цвета, которые вы хотите, которые максимально удалены друг от друга!
Если больше думать об этой проблеме, то было бы лучше отобразить цвета линейно, возможно, (0,0,0) → (255,255,255) лексикографически, а затем распределить их равномерно.
Я действительно не знаю, насколько хорошо это будет работать, но с тех пор, скажем так:
n = 10
мы знаем, что у нас 16777216 цветов (256^3).
Мы можем использовать Buckles Algorithm 515, чтобы найти лексикографически индексированный цвет.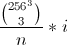
, Вам, вероятно, придется отредактировать алгоритм, чтобы избежать переполнения и, возможно, добавить некоторые незначительные улучшения скорости.
Было бы лучше найти цвета, максимально удаленные в "перцепционно однородном" цветовом пространстве, например, CIELAB (используя евклидово расстояние между координатами L*, a*, b* в качестве метрики расстояния), а затем преобразовать в цветовое пространство по вашему выбору. Однородность восприятия достигается путем настройки цветового пространства для аппроксимации нелинейностей в зрительной системе человека.
Некоторые связанные ресурсы:
ColorBrewer - наборы цветов, разработанные так, чтобы они были максимально различимы для использования на картах.
Выход из RGBland: выбор цветов для статистической графики - технический отчет, описывающий набор алгоритмов для генерации хороших (то есть максимально различимых) наборов цветов в цветовом пространстве hcl.
Вот некоторый код для равномерного распределения цветов RGB вокруг цветового круга HSL заданной яркости.
class cColorPicker
{
public:
void Pick( vector<DWORD>&v_picked_cols, int count, int bright = 50 );
private:
DWORD HSL2RGB( int h, int s, int v );
unsigned char ToRGB1(float rm1, float rm2, float rh);
};
/**
Evenly allocate RGB colors around HSL color wheel
@param[out] v_picked_cols a vector of colors in RGB format
@param[in] count number of colors required
@param[in] bright 0 is all black, 100 is all white, defaults to 50
based on Fig 3 of http://epub.wu-wien.ac.at/dyn/virlib/wp/eng/mediate/epub-wu-01_c87.pdf?ID=epub-wu-01_c87
*/
void cColorPicker::Pick( vector<DWORD>&v_picked_cols, int count, int bright )
{
v_picked_cols.clear();
for( int k_hue = 0; k_hue < 360; k_hue += 360/count )
v_picked_cols.push_back( HSL2RGB( k_hue, 100, bright ) );
}
/**
Convert HSL to RGB
based on http://www.codeguru.com/code/legacy/gdi/colorapp_src.zip
*/
DWORD cColorPicker::HSL2RGB( int h, int s, int l )
{
DWORD ret = 0;
unsigned char r,g,b;
float saturation = s / 100.0f;
float luminance = l / 100.f;
float hue = (float)h;
if (saturation == 0.0)
{
r = g = b = unsigned char(luminance * 255.0);
}
else
{
float rm1, rm2;
if (luminance <= 0.5f) rm2 = luminance + luminance * saturation;
else rm2 = luminance + saturation - luminance * saturation;
rm1 = 2.0f * luminance - rm2;
r = ToRGB1(rm1, rm2, hue + 120.0f);
g = ToRGB1(rm1, rm2, hue);
b = ToRGB1(rm1, rm2, hue - 120.0f);
}
ret = ((DWORD)(((BYTE)(r)|((WORD)((BYTE)(g))<<8))|(((DWORD)(BYTE)(b))<<16)));
return ret;
}
unsigned char cColorPicker::ToRGB1(float rm1, float rm2, float rh)
{
if (rh > 360.0f) rh -= 360.0f;
else if (rh < 0.0f) rh += 360.0f;
if (rh < 60.0f) rm1 = rm1 + (rm2 - rm1) * rh / 60.0f;
else if (rh < 180.0f) rm1 = rm2;
else if (rh < 240.0f) rm1 = rm1 + (rm2 - rm1) * (240.0f - rh) / 60.0f;
return static_cast<unsigned char>(rm1 * 255);
}
int _tmain(int argc, _TCHAR* argv[])
{
vector<DWORD> myCols;
cColorPicker colpick;
colpick.Pick( myCols, 20 );
for( int k = 0; k < (int)myCols.size(); k++ )
printf("%d: %d %d %d\n", k+1,
( myCols[k] & 0xFF0000 ) >>16,
( myCols[k] & 0xFF00 ) >>8,
( myCols[k] & 0xFF ) );
return 0;
}
Разве это не тот фактор, в каком порядке вы устанавливаете цвета?
Например, если вы используете идею Дилли-Ос, вам нужно как можно больше смешивать цвета. 0 64 128 256 - от одного к другому. но 0 256 64 128 в колесе было бы более "врозь"
Имеет ли это смысл?
Я читал где-то, что человеческий глаз не может различить менее 4 значений друг от друга. так что это что-то иметь в виду. Следующий алгоритм не компенсирует это.
Я не уверен, что это именно то, что вы хотите, но это один из способов случайного генерирования неповторяющихся значений цвета:
(будьте осторожны, псевдокод вперед непоследователен)
//colors entered as 0-255 [R, G, B]
colors = []; //holds final colors to be used
rand = new Random();
//assumes n is less than 16,777,216
randomGen(int n){
while (len(colors) < n){
//generate a random number between 0,255 for each color
newRed = rand.next(256);
newGreen = rand.next(256);
newBlue = rand.next(256);
temp = [newRed, newGreen, newBlue];
//only adds new colors to the array
if temp not in colors {
colors.append(temp);
}
}
}
Один из способов оптимизировать это для лучшей видимости - сравнить расстояние между каждым новым цветом и всеми цветами в массиве:
for item in color{
itemSq = (item[0]^2 + item[1]^2 + item[2]^2])^(.5);
tempSq = (temp[0]^2 + temp[1]^2 + temp[2]^2])^(.5);
dist = itemSq - tempSq;
dist = abs(dist);
}
//NUMBER can be your chosen distance apart.
if dist < NUMBER and temp not in colors {
colors.append(temp);
}
Но такой подход значительно замедлит ваш алгоритм.
Другим способом было бы исключить случайность и систематически проходить через каждые 4 значения и добавлять цвет к массиву в приведенном выше примере.
Я знаю, что это старый пост, но я нашел его, когда искал решение PHP для этой темы, и, наконец, пришел с простым решением:
function random_color($i = null, $n = 10, $sat = .5, $br = .7) {
$i = is_null($i) ? mt_rand(0,$n) : $i;
$rgb = hsv2rgb(array($i*(360/$n), $sat, $br));
for ($i=0 ; $i<=2 ; $i++)
$rgb[$i] = dechex(ceil($rgb[$i]));
return implode('', $rgb);
}
function hsv2rgb($c) {
list($h,$s,$v)=$c;
if ($s==0)
return array($v,$v,$v);
else {
$h=($h%=360)/60;
$i=floor($h);
$f=$h-$i;
$q[0]=$q[1]=$v*(1-$s);
$q[2]=$v*(1-$s*(1-$f));
$q[3]=$q[4]=$v;
$q[5]=$v*(1-$s*$f);
return(array($q[($i+4)%6]*255,$q[($i+2)%6]*255,$q[$i%6]*255)); //[1]
}
}
Так что просто вызовите функцию random_color(), где $ i определяет цвет, $ n количество возможных цветов, $ sat насыщенность и $ br яркость.
Для достижения "наиболее различимых" нам нужно использовать воспринимаемое цветовое пространство, такое как Lab (или любое другое воспринимаемое линейное цветовое пространство), а не RGB. Кроме того, мы можем квантовать это пространство, чтобы уменьшить размер пространства.
Создайте полное трехмерное пространство со всеми возможными квантованными записями и запустите алгоритм K-средних с k=N, Полученные центры / "средства" должны быть примерно максимально различимы друг от друга.