Левая куча двух версий создания реализации

Question

Недавно я читал книгу "Чисто-функциональные структуры данных", когда пришел к "Упражнению 3.2 Определить вставку напрямую, а не посредством вызова слияния" для Leftist_tree. Я реализую вставку моей версии.

 let rec insert x t =
try
  match t with
| E -> T (1, x, E, E)
| T (_, y, left, right ) ->
  match (Elem.compare x y) with
  | n when n < 0 -> makeT x left (insert y right)
  | 0 -> raise Same_elem
  | _ -> makeT y left (insert x right)
with
     Same_elem -> t

И для проверки, работает ли это, я проверяю это и функцию слияния, предлагаемую книгой.

 let rec merge m n = match (m, n) with
| (h, E) -> h
| (E, h) -> h 
| (T (_, x, a1, b1) as h1, (T (_, y, a2, b2) as h2)) ->
  if (Elem.compare x y) < 0
  then makeT x a1 (merge b1 h2)
  else makeT y a2 (merge b2 h1)

Тогда я нашел интересную вещь. Я использовал список ["a";"b";"d";"g";"z";"e";"c"] в качестве входных данных для создания этого дерева. И два результата разные. Для метода слияния я получил дерево вот так:

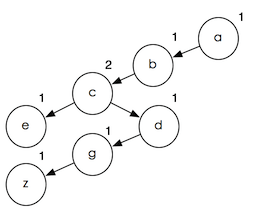
и метод вставки, который я реализовал, дает мне дерево вроде этого:

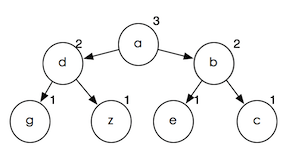
Я думаю, что есть некоторые детали между этими двумя методами, хотя я следую за реализацией 'слияния', чтобы спроектировать версию 'вставки'. Но затем я попробовал список, обратный ["c"; "e"; "z"; "g"; "d"; "b"; "a"], который дал мне два дерева слева-дерево-вставка. Это действительно смутило меня настолько, что я не знаю, является ли мой метод вставки неправильным или правильным. Итак, теперь у меня есть два вопроса:

1. если мой метод вставки неверен?
2. левое дерево за слиянием и левое дерево за вставкой - это одна и та же структура? Я имею в виду, что этот результат дает мне иллюзию, будто они равны в одном смысле.

весь код

module type Comparable = sig
    type t
    val compare : t -> t -> int
end

module LeftistHeap(Elem:Comparable) = struct
    exception Empty
    exception Same_elem

    type heap = E | T of int * Elem.t * heap * heap  

    let rank = function 
       | E -> 0
       | T (r ,_ ,_ ,_ ) -> r

    let makeT x a b =
       if rank a >= rank b
       then T(rank b + 1, x, a, b)
       else T(rank a + 1, x, b, a)

    let rec merge m n = match (m, n) with
       | (h, E) -> h
       | (E, h) -> h 
       | (T (_, x, a1, b1) as h1, (T (_, y, a2, b2) as h2)) ->
       if (Elem.compare x y) < 0
       then makeT x a1 (merge b1 h2)
       else makeT y a2 (merge b2 h1)

    let insert_merge x h = merge (T (1, x, E, E)) h

    let rec insert x t =
    try
        match t with
        | E -> T (1, x, E, E)
        | T (_, y, left, right ) ->
        match (Elem.compare x y) with
        | n when n < 0 -> makeT x left (insert y right)
        | 0 -> raise Same_elem
        | _ -> makeT y left (insert x right)
    with
        Same_elem -> t

    let rec creat_l_heap f = function 
        | [] -> E
        | h::t -> (f h (creat_l_heap f t))

    let create_merge l = creat_l_heap insert_merge l 
    let create_insert l = creat_l_heap insert l
end;;

module IntLeftTree = LeftistHeap(String);;

open IntLeftTree;;

let l = ["a";"b";"d";"g";"z";"e";"c"];;
let lh = create_merge `enter code here`l;;
let li = create_insert l;;

let h = ["c";"e";"z";"g";"d";"b";"a"];;
let hh = create_merge h;;
let hi = create_insert h;;

---

16. Октябрь 2015 обновление

более точно наблюдая две реализации, легко обнаружить, что различие заключалось в объединении базового дерева. T (1, x, E, E) или вставьте элемент x Я использовал график, который можно выразить более четко.

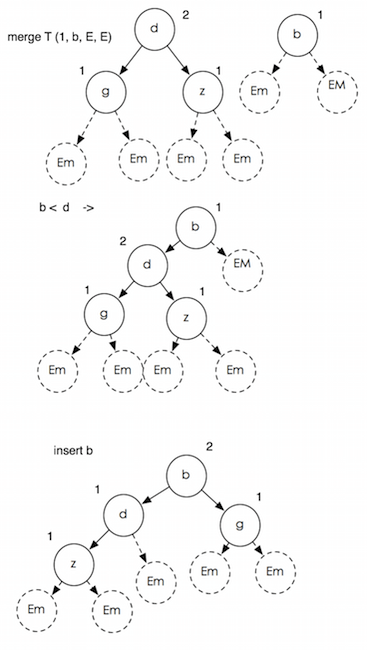
Итак, я обнаружил, что моя версия вставки всегда будет использовать больше сложности для завершения своей работы и не использует преимущества левого дерева, или она всегда работает в худшей ситуации, даже если эта древовидная структура в точности "левая".

и если я изменил небольшую часть, два кода получат одинаковый результат.

let rec insert x t =
  try
  match t with
  | E -> T (1, x, E, E)
  | T (_, y, left, right ) ->
    match (Elem.compare x y) with
    | n when n < 0 -> makeT x E t
    | 0 -> raise Same_elem
    | _ -> makeT y left (insert x right)
with
  Same_elem -> t

Итак, на мой первый вопрос: я думаю, что ответ не точный. он может действительно построить левое дерево, но всегда работать в плохой ситуации.

а второй вопрос немного бессмысленный (я не уверен). Но это все еще интересно для этого условия. например, хотя версия слияния работает более эффективно, но для построения дерева из списка без необходимости в порядке вставки, как я упоминал (["a";"b";"d";"g";"z";"e";"c"], ["c";"e";"z";"g";"d";"b";"a"], если порядок не важен, для меня я думаю, что они являются одним и тем же набором.) Функция слияния не может выбрать лучшее решение. (Я думаю, что древовидная структура ["a"; "b"; "d"; "g"; "z"; "e"; "c"] лучше, чем ["c"; "e"; " z ";" g ";" d ";" b ";" a "] s)

так что теперь мой вопрос:

1. Является ли древовидная структура, в которой каждый правый корешок пуст, - это хорошая структура?
2. если да, мы всегда можем построить его в любом порядке ввода?

Answer 1

Дерево с каждым пустым правым корешком - это просто список. Как таковой простой список является лучшей структурой для списка. Свойства среды выполнения будут такими же, как список, то есть для вставки, например, потребуется O(n) время вместо желаемого O(log n) время.

Для дерева обычно требуется сбалансированное дерево, в котором все дочерние узлы в идеале имеют одинаковый размер. В вашем коде каждый узел имеет rank и цель состоит в том, чтобы иметь одинаковый ранг для левой и правой стороны каждого узла. Если у вас нет точно 2^n - 1 записи в дереве это невозможно, и вы должны допустить некоторый дисбаланс в дереве. Обычно разница в ранге 1 или 2 допускается. Вставка должна вставить элемент на стороне с меньшим рангом, а удаление должно перебалансировать любой узел, который превышает допустимую разность рангов. Это сохраняет дерево достаточно сбалансированным, обеспечивая сохранение требуемых свойств времени выполнения.

Проверьте ваш учебник, какая разница в ранге допускается в вашем случае.