Напишите программу, чтобы найти 100 самых больших чисел из массива в 1 миллиард чисел
Недавно я посетил интервью, где меня попросили "написать программу, чтобы найти 100 самых больших чисел из массива в 1 миллиард чисел".
Я смог дать только решение методом грубой силы, которое должно было отсортировать массив за O(nlogn) сложность времени и взять последние 100 чисел.
Arrays.sort(array);
Интервьюер искал лучшую временную сложность, я попробовал пару других решений, но не смог ему ответить. Есть ли лучшее решение сложности времени?
32 ответа
Вы можете сохранить приоритетную очередь из 100 самых больших чисел, перебирать миллиардные числа, всякий раз, когда вы встречаете число, превышающее наименьшее число в очереди (заголовок очереди), удаляете заголовок очереди и добавляете новый номер. в очередь.
РЕДАКТИРОВАТЬ: как отметил Dev, с приоритетной очереди, реализованной с кучей, сложность вставки в очередь O(logN)
В худшем случае вы получите billionlog2(100) что лучше чем billionlog2(billion)
В общем, если вам нужны самые большие K чисел из набора из N чисел, сложность O(NlogK) скорее, чем O(NlogN), это может быть очень значительным, когда K очень мало по сравнению с N.
EDIT2:
Ожидаемое время этого алгоритма довольно интересно, поскольку на каждой итерации вставка может происходить или не происходить. Вероятность того, что i-е число будет вставлено в очередь, - это вероятность того, что случайная величина будет больше, чем, по крайней мере, i-K случайные величины из одного и того же распределения (первые k чисел автоматически добавляются в очередь). Мы можем использовать статистику заказов (см. Ссылку), чтобы рассчитать эту вероятность. Например, давайте предположим, что числа были случайно выбраны равномерно из {0, 1}ожидаемое значение (iK) -ого числа (из числа i) (i-k)/iи вероятность того, что случайная величина будет больше этого значения, равна 1-[(i-k)/i] = k/i,
Таким образом, ожидаемое количество вставок составляет:
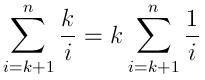
И ожидаемое время работы может быть выражено как:
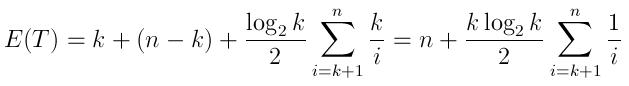
(k время генерировать очередь с первым k элементы, то n-k сравнения и ожидаемое количество вставок, как описано выше, каждая занимает в среднем log(k)/2 время)
Обратите внимание, что когда N очень большой по сравнению с Kэто выражение намного ближе к n скорее, чем NlogK, Это несколько интуитивно понятно, так как в случае вопроса даже после 10000 итераций (что очень мало по сравнению с миллиардом) вероятность того, что число будет вставлено в очередь, очень мала.
Если об этом спрашивают в интервью, я думаю, что интервьюер, вероятно, хочет видеть ваш процесс решения проблем, а не только ваши знания алгоритмов.
Описание довольно общее, так что, возможно, вы можете задать ему диапазон или значение этих чисел, чтобы прояснить проблему. Это может произвести впечатление на интервьюера. Если, например, эти цифры соответствуют возрасту людей внутри страны (например, Китая), то это гораздо более простая проблема. С разумным допущением, что никто не живет старше 200 лет, вы можете использовать массив int размером 200(может быть, 201), чтобы подсчитать количество людей одного возраста за одну итерацию. Здесь индекс означает возраст. После этого это кусок пирога, чтобы найти 100 наибольшее число. Кстати, этот алгоритм называется счетной сортировкой.
В любом случае, сделать интервью более конкретным и ясным - это хорошо для вас.
Вы можете перебирать числа, которые занимают O(n)
Всякий раз, когда вы найдете значение, превышающее текущий минимум, добавьте новое значение в круговую очередь размером 100.
Минут этой круговой очереди - ваше новое значение сравнения. Продолжайте добавлять в эту очередь. Если заполнено, извлеките минимум из очереди.
Я понял, что это помечено как "алгоритм", но выбрасывает некоторые другие варианты, поскольку, вероятно, также следует пометить "интервью".
Каков источник 1 миллиарда чисел? Если это база данных, то "выбор значения из порядка таблиц по значению desc limit 100" прекрасно справился бы с этой задачей - могут существовать различия в диалектах.
Это одноразовое или что-то, что будет повторяться? Если повторяется, как часто? Если это одноразовый файл и данные находятся в файле, то 'cat srcfile | сортировать (варианты по необходимости) | head -100'позволит вам быстро выполнять продуктивную работу, за которую вам платят, в то время как компьютер справляется с этой тривиальной работой.
Если это будет повторяться, вы посоветуете выбрать любой подходящий подход, чтобы получить первоначальный ответ и сохранить / кэшировать результаты, чтобы вы могли непрерывно иметь возможность сообщать о лучших 100.
Наконец, есть это соображение. Вы ищете работу начального уровня и проводите собеседования с вычурным менеджером или будущим коллегой? Если это так, то вы можете отказаться от всех подходов, описывающих относительные технические плюсы и минусы. Если вы ищете более управленческую работу, то подходите к ней так, как это сделал бы менеджер, связанный с затратами на разработку и обслуживание решения, и говорите "большое спасибо", и уходите, если это интервьюер хочет сосредоточиться на мелочах CS, У него и у вас вряд ли будет большой потенциал продвижения вперед.
Удачи на следующем интервью.
Моей непосредственной реакцией на это было бы использование кучи, но есть способ использовать QuickSelect, не сохраняя все входные значения под рукой одновременно.
Создайте массив размером 200 и заполните его первыми 200 входными значениями. Запустите QuickSelect и откажитесь от низких 100, оставив вам 100 свободных мест. Прочитайте следующие 100 входных значений и снова запустите QuickSelect. Продолжайте до тех пор, пока вы не выполните все входные данные партиями по 100 штук.
В конце у вас есть 100 лучших значений. Для значений N вы запустили QuickSelect примерно N/100 раз. Стоимость каждого быстрого выбора примерно в 200 раз превышает некоторую постоянную, поэтому общая стоимость в 2N раза превышает некоторую постоянную. Это выглядит линейно по размеру входных данных для меня, независимо от размера параметра, который я собираюсь установить равным 100 в этом объяснении.
Вы можете использовать алгоритм быстрого выбора, чтобы найти число по индексу (по порядку) [billion-101], а затем выполнить итерацию по числам и найти числа, которые больше этого числа.
array={...the billion numbers...}
result[100];
pivot=QuickSelect(array,billion-101);//O(N)
for(i=0;i<billion;i++)//O(N)
if(array[i]>=pivot)
result.add(array[i]);
Время этого алгоритма: 2 X O(N) = O(N) (средняя производительность по случаю)
Второй вариант, предложенный Томасом Юнгблутом:
При построении кучи максимальная куча будет занимать O (N), затем верхние 100 максимальных чисел будут в верхней части кучи, все, что вам нужно, это вытащить их из кучи (100 X O(Log(N))).
Время этого алгоритма:O(N) + 100 X O(Log(N)) = O(N)
Хотя другое решение для быстрого выбора было отклонено, факт остается фактом, что быстрый выбор найдет решение быстрее, чем использование очереди размером 100. У быстрого выбора есть ожидаемое время выполнения 2n + o(n), с точки зрения сравнений. Очень просто реализация будет
array = input array of length n
r = Quickselect(array,n-100)
result = array of length 100
for(i = 1 to n)
if(array[i]>r)
add array[i] to result
Это займет 3n + o(n) сравнений в среднем. Более того, это можно сделать более эффективным, используя тот факт, что быстрый выбор оставит 100 самых больших элементов в массиве в 100 самых правых местах. Таким образом, время выполнения может быть улучшено до 2n+o(n).
Существует проблема, что, как ожидается, время работы, и не худший случай, но с использованием стратегии приличной выбора поворота (например, выбрать 21 элементов в случайном порядке, и выбрать медиану этих 21 в качестве оси), то число сравнений может быть гарантируется с высокой вероятностью не более (2+c)n для сколь угодно малой постоянной c.
Фактически, используя оптимизированную стратегию выборки (например, выборку элементов sqrt(n) случайным образом и выбор 99-го процентиля), время выполнения может быть уменьшено до (1+c)n + o(n) для сколь угодно малого c (при условии, что K, количество элементов, которые будут выбраны, o(n)).
С другой стороны, использование очереди размером 100 потребует O(log(100)n) сравнений, а база журналов 2 из 100 приблизительно равна 6,6.
Если мы подумаем об этой проблеме в более абстрактном смысле, выбирая самые большие элементы K из массива размера N, где K=o(N), но оба K и N уходят в бесконечность, тогда время работы версии быстрого выбора будет O(N) и версия очереди будет O(N log K), поэтому в этом смысле быстрый выбор также асимптотически превосходит.
В комментариях было упомянуто, что решение очереди будет запущено в ожидаемое время N + K log N на случайном входе. Конечно, предположение о случайном вводе никогда не будет действительным, если вопрос не сформулирован явно. Решение очереди может быть сделано для обхода массива в случайном порядке, но это потребует дополнительных затрат на N вызовов генератора случайных чисел, а также либо перестановки всего входного массива, либо выделения нового массива длиной N, содержащего случайные индексы.
Если проблема не позволяет вам перемещаться по элементам в исходном массиве, а стоимость выделения памяти высока, поэтому дублирование массива не вариант, это другой вопрос. Но строго с точки зрения времени работы, это лучшее решение.
Возьмите первые 100 номеров миллиарда и рассортируйте их. Теперь просто переберите миллиард, если номер источника больше, чем наименьшее из 100, вставьте в порядке сортировки. То, что вы в итоге получите, будет намного ближе к O(n) по размеру набора.
Очень простым решением было бы перебрать массив 100 раз. Который O(n),
Каждый раз, когда вы вытаскиваете наибольшее число (и меняете его значение на минимальное значение, чтобы вы не видели его на следующей итерации или не отслеживали индексы предыдущих ответов (отслеживая индексы, исходный массив может иметь кратно одному и тому же номеру)). После 100 итераций вы получите 100 самых больших чисел.
Два варианта:
(1) куча (приоритетная очередь)
Поддерживайте минимальную кучу размером 100. Пройдите через массив. Как только элемент станет меньше первого элемента в куче, замените его.
InSERT ELEMENT INTO HEAP: O(log100)
compare the first element: O(1)
There are n elements in the array, so the total would be O(nlog100), which is O(n)
(2) Карта-уменьшенная модель.
Это очень похоже на пример подсчета слов в hadoop. Задание на карте: подсчитайте частоту или время каждого элемента. Уменьшить: получить верхний элемент К.
Обычно я бы дал рекрутеру два ответа. Дайте им все, что они хотят. Конечно, кодирование с уменьшением карты будет трудоемким, потому что вы должны знать все точные параметры. Не вредно практиковать это. Удачи.
Простым решением будет использование очереди с приоритетами, добавление первых 100 чисел в очередь и отслеживание наименьшего числа в очереди, затем итерация по другим миллиардам чисел, и каждый раз, когда мы находим одно, которое больше, чем наибольшее число в очереди с приоритетами мы удаляем наименьшее число, добавляем новый номер и снова отслеживаем наименьшее число в очереди.
Если бы числа были в случайном порядке, это работало бы прекрасно, потому что, поскольку мы перебираем миллиард случайных чисел, очень редко будет следующее число среди 100 самых больших до сих пор. Но цифры могут быть не случайными. Если массив уже отсортирован в порядке возрастания, мы всегда вставляем элемент в очередь с приоритетами.
Поэтому сначала мы выбираем, скажем, 100 000 случайных чисел из массива. Чтобы избежать случайного доступа, который может быть медленным, мы добавим, скажем, 400 случайных групп по 250 последовательных чисел. С помощью этого случайного выбора мы можем быть совершенно уверены, что очень немногие из оставшихся чисел входят в первую сотню, поэтому время выполнения будет очень близко к времени простого цикла, сравнивающего миллиард чисел с некоторым максимальным значением.
На этот вопрос будет дан ответ со сложностью N log(100) (вместо N log N) с одной строкой кода C++.
std::vector<int> myvector = ...; // Define your 1 billion numbers.
// Assumed integer just for concreteness
std::partial_sort (myvector.begin(), myvector.begin()+100, myvector.end());
Окончательным ответом будет вектор, в котором первые 100 элементов гарантированно будут 100 самыми большими числами вашего массива, а остальные элементы неупорядочены.
C++ STL (стандартная библиотека) весьма удобен для решения подобных задач.
Примечание: я не говорю, что это оптимальное решение, но оно спасло бы ваше интервью.
Вы можете сделать это в O(n) время. Просто перебирайте список и отслеживайте 100 самых больших чисел, которые вы видели в любой заданной точке, и минимальное значение в этой группе. Когда вы обнаружите, что новое число больше наименьшего из ваших десяти, замените его и обновите новое минимальное значение 100 (может потребоваться постоянное время, равное 100, чтобы определить это каждый раз, когда вы это делаете, но это не влияет на общий анализ).
Although in this question we should search for top 100 numbers, I will
generalize things and write x. Still, I will treat x as constant value.
Алгоритм Biggest x элементов из n:
Я назову возвращаемое значение LIST. Это набор элементов x (на мой взгляд, это должен быть связанный список)
- Первые элементы x берутся из пула "по мере их поступления" и сортируются в LIST (это делается за постоянное время, поскольку x рассматривается как постоянное время - O( x log(x)))
- Для каждого следующего элемента мы проверяем, является ли он больше, чем наименьший элемент в LIST, и, если это, вынимаем самый маленький элемент и вставляем текущий элемент в LIST. Поскольку это упорядоченный список, каждый элемент должен найти свое место в логарифмическом времени (бинарный поиск), и поскольку упорядоченный список не является проблемой, вставка не является проблемой. Каждый шаг также выполняется за постоянное время (O (log (x)).
Итак, каков наихудший сценарий?
x log(x) + (nx)(log(x)+1) = nlog(x) + n - x
Так что это O (N) время для худшего случая. +1 - это проверка, если число больше, чем наименьшее число в LIST. Ожидаемое время для среднего случая будет зависеть от математического распределения этих n элементов.
Возможные улучшения
Этот алгоритм может быть немного улучшен для наихудшего сценария, но ИМХО (я не могу доказать это утверждение), который ухудшит среднее поведение. Асимптотическое поведение будет таким же.
Улучшение в этом алгоритме будет заключаться в том, что мы не будем проверять, больше ли элемент, чем наименьший. Для каждого элемента мы попытаемся вставить его, и если он меньше, чем наименьший, мы проигнорируем его. Хотя это звучит нелепо, если мы рассмотрим только худший сценарий, который у нас будет
x log(x) + (nx)log(x) = nlog(x)
операции.
Для этого варианта использования я не вижу дальнейших улучшений. И все же вы должны спросить себя - что если мне придется делать это больше, чем log (n) раз и для разных x-es? Очевидно, что мы отсортировали бы этот массив в O (n log (n)) и взяли бы наш элемент x всякий раз, когда они нам нужны.
Поиск лучших 100 из миллиарда чисел лучше всего сделать, используя минимальную кучу из 100 элементов.
Сначала заполните мин-кучу первыми 100 встреченными числами. min-heap будет хранить наименьшее из первых 100 чисел в корне (вверху).
Теперь, когда вы идете вдоль остальных чисел, сравните их только с корнем (наименьшее из 100).
Если обнаруженное новое число больше, чем корень из min-heap, замените корень на это число, иначе проигнорируйте его.
Как часть вставки нового числа в min-heap наименьшее число в куче придет к вершине (root).
После того, как мы пройдем все числа, у нас будут самые большие 100 чисел в минимальной куче.
Вдохновленный ответом @ron teller, вот программа на Си, которая делает то, что вы хотите.
#include <stdlib.h>
#include <stdio.h>
#define TOTAL_NUMBERS 1000000000
#define N_TOP_NUMBERS 100
int
compare_function(const void *first, const void *second)
{
int a = *((int *) first);
int b = *((int *) second);
if (a > b){
return 1;
}
if (a < b){
return -1;
}
return 0;
}
int
main(int argc, char ** argv)
{
if(argc != 2){
printf("please supply a path to a binary file containing 1000000000"
"integers of this machine's wordlength and endianness\n");
exit(1);
}
FILE * f = fopen(argv[1], "r");
if(!f){
exit(1);
}
int top100[N_TOP_NUMBERS] = {0};
int sorts = 0;
for (int i = 0; i < TOTAL_NUMBERS; i++){
int number;
int ok;
ok = fread(&number, sizeof(int), 1, f);
if(!ok){
printf("not enough numbers!\n");
break;
}
if(number > top100[0]){
sorts++;
top100[0] = number;
qsort(top100, N_TOP_NUMBERS, sizeof(int), compare_function);
}
}
printf("%d sorts made\n"
"the top 100 integers in %s are:\n",
sorts, argv[1] );
for (int i = 0; i < N_TOP_NUMBERS; i++){
printf("%d\n", top100[i]);
}
fclose(f);
exit(0);
}
На моей машине (ядро i3 с быстрым SSD) это занимает 25 секунд и 1724 сортировки. Я сгенерировал бинарный файл с dd if=/dev/urandom/ count=1000000000 bs=1 для этого бега.
Очевидно, что есть проблемы с производительностью при чтении только 4 байтов за раз - с диска, но это ради примера. С положительной стороны, очень мало памяти требуется.
Самое простое решение - сканировать массив из миллиарда чисел и хранить 100 самых больших значений, найденных до сих пор, в буфере небольшого массива без какой-либо сортировки и запоминать наименьшее значение этого буфера. Сначала я подумал, что этот метод был предложен fordprefect, но в комментарии он сказал, что он предполагает реализацию структуры данных из 100 чисел в виде кучи. Всякий раз, когда обнаруживается новое число, которое больше минимума в буфере, перезаписывается новым найденным значением, и в буфере снова выполняется поиск текущего минимума. Если числа в массиве миллиардов чисел распределяются случайным образом большую часть времени, значение из большого массива сравнивается с минимумом маленького массива и отбрасывается. Только для очень очень маленькой доли числа значение должно быть вставлено в маленький массив. Таким образом, разница в манипулировании структурой данных, содержащей маленькие числа, может игнорироваться. Для небольшого числа элементов трудно определить, является ли использование очереди приоритетов на самом деле более быстрым, чем использование моего наивного подхода.
Я хочу оценить количество вставок в небольшой буфер массива из 100 элементов при сканировании массива из 10^9 элементов. Программа сканирует первые 1000 элементов этого большого массива и должна вставить в буфер не более 1000 элементов. Буфер содержит 100 элементов из 1000 отсканированных элементов, то есть 0,1 отсканированного элемента. Поэтому мы предполагаем, что вероятность того, что значение из большого массива будет больше, чем текущий минимум буфера, составляет около 0,1. Такой элемент должен быть вставлен в буфер. Теперь программа сканирует следующие 10^4 элементов из большого массива. Поскольку минимум буфера будет увеличиваться каждый раз, когда вставляется новый элемент. Мы подсчитали, что соотношение элементов больше нашего текущего минимума составляет около 0,1, и поэтому для вставки требуется 0,1*10^4=1000 элементов. На самом деле ожидаемое количество элементов, которые вставляются в буфер, будет меньше. После сканирования этих 10^4 элементов доля чисел в буфере составит около 0,01 от сканированных элементов. Поэтому при сканировании следующих 10^5 чисел мы предполагаем, что в буфер будет вставлено не более 0,01*10^5=1000. Продолжая эту аргументацию, мы вставили около 7000 значений после сканирования 1000+10^4+10^5+...+10^9 ~ 10^9 элементов большого массива. Поэтому при сканировании массива с 10^9 элементами случайного размера мы ожидаем не более 10^4 (=7000 округленных) вставок в буфер. После каждой вставки в буфер должен быть найден новый минимум. Если буфер представляет собой простой массив, нам нужно 100 сравнений, чтобы найти новый минимум. Если буфер представляет собой другую структуру данных (например, кучу), нам нужно как минимум 1 сравнение, чтобы найти минимум. Чтобы сравнить элементы большого массива, нам нужно 10^9 сравнений. Таким образом, в целом нам нужно около 10^9+100*10^4=1.001 * 10^9 сравнений при использовании массива в качестве буфера и как минимум 1.000 * 10^9 сравнений при использовании другого типа структуры данных (например, кучи), Таким образом, использование кучи приносит только 0,1% прироста, если производительность определяется числом сравнений. Но какова разница во времени выполнения между вставкой элемента в кучу из 100 элементов и заменой элемента в массиве из 100 элементов и поиском его нового минимума?
На теоретическом уровне: сколько сравнений необходимо для вставки в кучу. Я знаю, что это O(log(n)), но насколько велик постоянный фактор? я
На машинном уровне: Какое влияние оказывают кэширование и прогноз ветвления на время выполнения вставки кучи и линейного поиска в массиве.
На уровне реализации: Какие дополнительные затраты скрыты в структуре данных кучи, предоставляемой библиотекой или компилятором?
Я думаю, что это некоторые из вопросов, на которые необходимо ответить, прежде чем можно будет попытаться оценить реальную разницу между производительностью кучи из 100 элементов или массива из 100 элементов. Поэтому имеет смысл провести эксперимент и измерить реальную производительность.
Я вижу много O(N) обсуждений, поэтому я предлагаю что-то другое только для упражнения мысли.
Есть ли какая-либо известная информация о природе этих чисел? Если это случайный характер, то не идите дальше и посмотрите на другие ответы. Вы не получите лучшие результаты, чем они.
Тем не мение! Посмотрите, заполняет ли какой-либо механизм заполнения списков этот список в определенном порядке. Находятся ли они в четко определенной схеме, в которой вы можете с уверенностью знать, что наибольшая величина чисел будет найдена в определенной области списка или в определенном интервале? Там может быть образец для этого. Если это так, например, если они гарантированно находятся в каком-то нормальном распределении с характерным горбом в середине, всегда имеют повторяющиеся восходящие тренды среди определенных подмножеств, имеют продолжительный всплеск в некоторый момент времени T в середине данных установите, например, частоту случаев инсайдерской торговли или отказа оборудования, или, возможно, просто поставьте "пик" на каждое N-е число, так как при анализе сил после катастрофы вы можете значительно сократить количество записей, которые вы должны проверить.
В любом случае, есть пища для размышлений. Возможно, это поможет вам дать будущим интервьюерам вдумчивый ответ. Я знаю, что был бы впечатлен, если бы кто-то задал мне такой вопрос в ответ на такую проблему, как это, - он сказал бы, что они думают об оптимизации. Просто осознайте, что не всегда есть возможность оптимизировать.
Я бы выяснил, у кого было время собрать миллиард чисел в массив и уволить его. Должен работать на правительство. По крайней мере, если бы у вас был связанный список, вы могли бы вставить число в середину, не сдвигая полмиллиарда, чтобы освободить место. Еще лучше Btree позволяет бинарный поиск. Каждое сравнение устраняет половину вашей суммы. Алгоритм хеширования позволит вам заполнить структуру данных как шахматную доску, но не так хорошо для разреженных данных. Лучше всего иметь массив решений из 100 целых чисел и следить за наименьшим числом в массиве решений, чтобы вы могли заменить его, когда натолкнетесь на большее число в исходном массиве. Вам придется посмотреть на каждый элемент в исходном массиве, предполагая, что он не отсортирован с самого начала.
Сначала возьмите 1000 элементов и добавьте их в максимальную кучу. Теперь возьмите первые 100 элементов и сохраните их где-нибудь. Теперь выберите следующие 900 элементов из файла и добавьте их в кучу вместе с последними 100 самыми старшими элементами.
Продолжайте повторять этот процесс, собирая 100 элементов из кучи и добавляя 900 элементов из файла.
Окончательный выбор из 100 элементов даст нам максимум 100 элементов из миллиарда чисел.
Time ~ O(100 * N)
Space ~ O(100 + N)
Создать пустой список из 100 пустых слотов
Для каждого номера в списке ввода:
Если число меньше первого, пропустите
В противном случае замените его на этот номер
Затем нажмите номер через соседний своп; пока он не станет меньше следующего
Вернуть список
Примечание: если log(input-list.size) + c < 100Тогда оптимальным способом будет сортировка входного списка, а затем разделение первых 100 элементов.
Другой алгоритм O(n) -
Алгоритм находит наибольшее 100 по исключению
Рассмотрим все миллионы чисел в их двоичном представлении. Начните с самого значительного бита. Выяснение, является ли MSB 1, может быть сделано умножением логической операции с соответствующим числом. Если в этих миллионах больше 100 единиц, то остальные цифры с нулями исключите. Теперь из оставшихся чисел перейдем к следующему наиболее значимому биту. ведите подсчет количества оставшихся чисел после исключения и продолжайте, пока это число больше 100.
Основная логическая операция может выполняться параллельно на графических процессорах.
Возможные улучшения.
Если файл содержит 1 миллиардное число, чтение может быть очень долгим...
Чтобы улучшить эту работу, вы можете:
- Разделите файл на n частей, создайте n потоков, заставьте n потоков искать по 100 самых больших чисел в своей части файла (используя очередь с приоритетами) и, наконец, получить 100 самых больших чисел из всех выходных потоков.
- Используйте кластер для выполнения такой задачи с помощью решения, подобного hadoop. Здесь вы можете разделить файл еще больше и получить более быстрый вывод для файла с 1 миллиардом (или 10^12) чисел.
- Используйте n-й элемент, чтобы получить 100-й элемент O(n)
- Повторяйте второй раз, но только один раз и выводите каждый элемент, который больше, чем этот конкретный элемент.
Пожалуйста, обратите внимание esp. второй шаг может быть легко вычислен параллельно! И это также будет эффективно, когда вам нужен миллион самых больших элементов.
Это вопрос от Google или других гигантов отрасли. Возможно, следующий код - правильный ответ, ожидаемый вашим интервьюером. Стоимость времени и стоимость пространства зависят от максимального числа во входном массиве. Для 32-битного ввода массива int, максимальная стоимость пространства составляет 4 * 125M байт, стоимость времени составляет 5 * млрд.
public class TopNumber {
public static void main(String[] args) {
final int input[] = {2389,8922,3382,6982,5231,8934
,4322,7922,6892,5224,4829,3829
,6892,6872,4682,6723,8923,3492};
//One int(4 bytes) hold 32 = 2^5 value,
//About 4 * 125M Bytes
//int sort[] = new int[1 << (32 - 5)];
//Allocate small array for local test
int sort[] = new int[1000];
//Set all bit to 0
for(int index = 0; index < sort.length; index++){
sort[index] = 0;
}
for(int number : input){
sort[number >>> 5] |= (1 << (number % 32));
}
int topNum = 0;
outer:
for(int index = sort.length - 1; index >= 0; index--){
if(0 != sort[index]){
for(int bit = 31; bit >= 0; bit--){
if(0 != (sort[index] & (1 << bit))){
System.out.println((index << 5) + bit);
topNum++;
if(topNum >= 3){
break outer;
}
}
}
}
}
}
}
Я написал простое решение на Python на случай, если кому-то будет интересно. Он использует bisect модуль и временный список возврата, который он хранит отсортированным. Это похоже на реализацию очереди с приоритетами.
import bisect
def kLargest(A, k):
'''returns list of k largest integers in A'''
ret = []
for i, a in enumerate(A):
# For first k elements, simply construct sorted temp list
# It is treated similarly to a priority queue
if i < k:
bisect.insort(ret, a) # properly inserts a into sorted list ret
# Iterate over rest of array
# Replace and update return array when more optimal element is found
else:
if a > ret[0]:
del ret[0] # pop min element off queue
bisect.insort(ret, a) # properly inserts a into sorted list ret
return ret
Использование с 100 000 000 элементов и вводом в худшем случае, который представляет собой отсортированный список:
>>> from so import kLargest
>>> kLargest(range(100000000), 100)
[99999900, 99999901, 99999902, 99999903, 99999904, 99999905, 99999906, 99999907,
99999908, 99999909, 99999910, 99999911, 99999912, 99999913, 99999914, 99999915,
99999916, 99999917, 99999918, 99999919, 99999920, 99999921, 99999922, 99999923,
99999924, 99999925, 99999926, 99999927, 99999928, 99999929, 99999930, 99999931,
99999932, 99999933, 99999934, 99999935, 99999936, 99999937, 99999938, 99999939,
99999940, 99999941, 99999942, 99999943, 99999944, 99999945, 99999946, 99999947,
99999948, 99999949, 99999950, 99999951, 99999952, 99999953, 99999954, 99999955,
99999956, 99999957, 99999958, 99999959, 99999960, 99999961, 99999962, 99999963,
99999964, 99999965, 99999966, 99999967, 99999968, 99999969, 99999970, 99999971,
99999972, 99999973, 99999974, 99999975, 99999976, 99999977, 99999978, 99999979,
99999980, 99999981, 99999982, 99999983, 99999984, 99999985, 99999986, 99999987,
99999988, 99999989, 99999990, 99999991, 99999992, 99999993, 99999994, 99999995,
99999996, 99999997, 99999998, 99999999]
Потребовалось около 40 секунд, чтобы рассчитать это для 100 000 000 элементов, поэтому я боюсь сделать это за 1 миллиард. Чтобы быть справедливым, хотя, я кормил его входом наихудшего случая (по иронии судьбы массив, который уже отсортирован).
Я сделал свой собственный код, не уверен, что это то, что "интервьюер" это смотрит
private static final int MAX=100;
PriorityQueue<Integer> queue = new PriorityQueue<>(MAX);
queue.add(array[0]);
for (int i=1;i<array.length;i++)
{
if(queue.peek()<array[i])
{
if(queue.size() >=MAX)
{
queue.poll();
}
queue.add(array[i]);
}
}
Задача: Найти m самых больших элементов из n элементов, где n >>> m
Самое простое решение, которое должно быть очевидно для всех, - это просто выполнить m проходов алгоритма сортировки пузырьков.
затем распечатайте последние n элементов массива.
Это не требует внешних структур данных и использует алгоритм, который всем известен.
Оценка времени выполнения O(m*n). Наилучшие ответы до сих пор - O(n log(m)), так что это решение не намного дороже для малых m.
Я не говорю, что это нельзя улучшить, но это, безусловно, самое простое решение.
Этот код предназначен для поиска N самых больших чисел в несортированном массиве.
#include <iostream>
using namespace std;
#define Array_Size 5 // No Of Largest Numbers To Find
#define BILLION 10000000000
void findLargest(int max[], int array[]);
int checkDup(int temp, int max[]);
int main() {
int array[BILLION] // contains data
int i=0, temp;
int max[Array_Size];
findLargest(max,array);
cout<< "The "<< Array_Size<< " largest numbers in the array are: \n";
for(i=0; i< Array_Size; i++)
cout<< max[i] << endl;
return 0;
}
void findLargest(int max[], int array[])
{
int i,temp,res;
for(int k=0; k< Array_Size; k++)
{
i=0;
while(i < BILLION)
{
for(int j=0; j< Array_Size ; j++)
{
temp = array[i];
res= checkDup(temp,max);
if(res == 0 && max[j] < temp)
max[j] = temp;
}
i++;
}
}
}
int checkDup(int temp, int max[])
{
for(int i=0; i<N_O_L_N_T_F; i++)
{
if(max[i] == temp)
return -1;
}
return 0;
}
Это не может быть эффективным, но делает работу.
Надеюсь это поможет
Я знаю, что это может быть похоронено, но вот моя идея для вариации на radix MSD,
pseudo-code:
//billion is the array of 1 billion numbers
int[] billion = getMyBillionNumbers();
//this assumes these are 32-bit integers and we are using hex digits
int[][] mynums = int[8][16];
for number in billion
putInTop100Array(number)
function putInTop100Array(number){
//basically if we got past all the digits successfully
if(number == null)
return true;
msdIdx = getMsdIdx(number);
msd = getMsd(number);
//check if the idx above where we are is already full
if(mynums[msdIdx][msd+1] > 99) {
return false;
} else if(putInTop100Array(removeMSD(number)){
mynums[msdIdx][msd]++;
//we've found 100 digits here, no need to keep looking below where we are
if(mynums[msdIdx][msd] > 99){
for(int i = 0; i < mds; i++){
//making it 101 just so we can tell the difference
//between numbers where we actually found 101, and
//where we just set it
mynums[msdIdx][i] = 101;
}
}
return true;
}
return false;
}
Функция getMsdIdx(int num) вернул бы индекс самой значимой цифры (ненулевой). Функция getMsd(int num) вернул бы самую значимую цифру. Функция removeMSD(int num) удалит наиболее значимую цифру из числа и вернет номер (или вернет ноль, если после удаления самой значащей цифры ничего не осталось).
Как только это будет сделано, все, что осталось, это пройти mynums захватить первые 100 цифр Это было бы что-то вроде:
int[] nums = int[100];
int idx = 0;
for(int i = 7; i >= 0; i--){
int timesAdded = 0;
for(int j = 16; j >=0 && timesAdded < 100; j--){
for(int k = mynums[i][j]; k > 0; k--){
nums[idx] += j;
timesAdded++;
idx++;
}
}
}
Я должен отметить, что, хотя вышеприведенное выглядит так, как будто оно имеет высокую временную сложность, оно действительно будет только вокруг O(7*100),
Краткое объяснение того, что это пытается сделать: По сути, эта система пытается использовать каждую цифру в 2-мерном массиве на основе индекса цифры в числе и ее значения. Он использует их в качестве индексов для отслеживания того, сколько чисел этого значения было вставлено в массив. Когда 100 достигнуто, оно закрывает все "нижние ветви".
Время этого алгоритма что-то вроде O(billion*log(16)*7)+O(100), Я могу ошибаться по этому поводу. Также весьма вероятно, что это требует отладки, поскольку это довольно сложно, и я просто написал это на макушке.
РЕДАКТИРОВАТЬ: Downvotes без объяснения причин не помогают. Если вы считаете этот ответ неверным, оставьте комментарий, почему. Я уверен, что Stackru даже скажет вам сделать это, когда вы понижаете голос.