Быстрый метод округления двойного к 32-битному int объяснил
Читая исходный код Lua, я заметил, что Lua использует macro округлить double к 32-битному int, Я извлек macroи это выглядит так:
union i_cast {double d; int i[2]};
#define double2int(i, d, t) \
{volatile union i_cast u; u.d = (d) + 6755399441055744.0; \
(i) = (t)u.i[ENDIANLOC];}
Вот ENDIANLOC определяется как порядковый номер, 0 для байтов, 1 для большого порядка Луа осторожно обращается с порядком байтов. t обозначает целочисленный тип, например int или же unsigned int,
Я сделал небольшое исследование, и есть более простой формат macro который использует ту же мысль:
#define double2int(i, d) \
{double t = ((d) + 6755399441055744.0); i = *((int *)(&t));}
Или в стиле C++:
inline int double2int(double d)
{
d += 6755399441055744.0;
return reinterpret_cast<int&>(d);
}
Этот трюк может работать на любой машине, использующей IEEE 754 (что означает практически любую машину сегодня). Он работает как для положительных, так и для отрицательных чисел, а округление следует правилу банкира. (Это не удивительно, поскольку следует IEEE 754.)
Я написал небольшую программу, чтобы проверить это:
int main()
{
double d = -12345678.9;
int i;
double2int(i, d)
printf("%d\n", i);
return 0;
}
И это выдает -12345679, как и ожидалось.
Хотелось бы подробнее узнать, как это сложно macro работает. Волшебный номер 6755399441055744.0 на самом деле 2^51 + 2^52, или же 1.5 * 2^52, а также 1.5 в двоичном виде можно представить как 1.1, Когда к этому магическому числу добавляется любое 32-разрядное целое число, я теряюсь отсюда. Как работает этот трюк?
PS: Это в исходном коде Lua, Llimits.h.
ОБНОВЛЕНИЕ:
- Как указывает @Mysticial, этот метод не ограничивается 32-битным
int, он также может быть расширен до 64-разрядногоintдо тех пор, пока число находится в диапазоне 2^52. (Themacroнуждается в некоторой модификации.) - В некоторых материалах говорится, что этот метод нельзя использовать в Direct3D.
При работе с ассемблером Microsoft для x86, есть еще быстрее
macroнаписано вassembly(это также извлечено из источника Lua):#define double2int(i,n) __asm {__asm fld n __asm fistp i}Для числа одинарной точности существует похожее магическое число:
1.5 * 2 ^23
4 ответа
double представляется так:
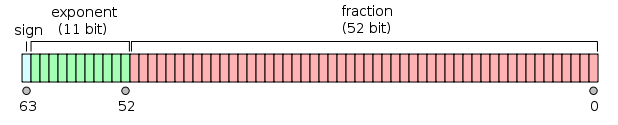
и это можно рассматривать как два 32-битных целых числа; теперь int принимается во всех версиях вашего кода (предположим, что это 32-разрядный int) справа на рисунке, так что в итоге вы просто берете 32 младших бита мантиссы.
Теперь к магическому номеру; как вы правильно сказали, 6755399441055744 - 2^51 + 2^52; добавление такого числа заставляет double перейти к "сладкому диапазону" между 2 ^ 52 и 2^53, который, как объясняется здесь в Википедии, обладает интересным свойством:
Между 252= 4,503,599,627,370,496 и 253= 9,007,199,254,740,992 представимые числа являются в точности целыми числами
Это следует из того, что мантисса имеет ширину 52 бита.
Другой интересный факт о добавлении 251+252 заключается в том, что он влияет на мантиссу только в двух старших битах, которые в любом случае отбрасываются, поскольку мы берем только его младшие 32 бита.
Последнее, но не менее важное: знак.
IEEE 754 с плавающей запятой использует величину и представление знака, в то время как целые числа на "нормальных" машинах используют арифметику дополнения 2; как это обрабатывается здесь?
Мы говорили только о натуральных числах; теперь предположим, что мы имеем дело с отрицательным числом в диапазоне, представленном 32-разрядным intтак меньше (по абсолютной величине) чем (-2^31+1); назови это -a, Такое число, очевидно, становится положительным, добавляя магическое число, и полученное значение равно 252+251+ (-a).
Теперь, что мы получим, если интерпретируем мантиссу в представлении дополнения 2? Он должен быть результатом суммы дополнения 2 (252+251) и (-a). Опять же, первый член влияет только на верхние два бита, а то, что остается в битах 0~50, является представлением дополнения 2 (-a) (опять же, минус два старших бита).
Поскольку уменьшение числа дополнения до 2 до меньшей ширины выполняется просто путем вырезания лишних битов слева, взятие младших 32 битов дает нам правильное значение (-a) в 32-битной арифметике дополнения 2.
Этот вид "уловки" исходит от старых процессоров x86, использующих инструкции / интерфейс 8087 для операций с плавающей запятой. На этих машинах есть инструкция для преобразования числа с плавающей запятой в целое число "кулак", но она использует текущий режим округления fp. К сожалению, спецификация C требует, чтобы преобразования fp->int усекались до нуля, в то время как все остальные операции fp
округлялись до ближайшего, поэтому для преобразования fp->int требуется сначала изменить режим округления fp, затем выполнить кулак, а затем восстановить fp режим округления.
Теперь на исходных 8086/8087 это было не так уж плохо, но на более поздних процессорах, которые начали получать суперскалярное и неупорядоченное выполнение, изменение режима округления fp, как правило, последовательное ядро процессора и довольно дорого. Таким образом, на таких процессорах, как Pentium-III или Pentium-IV, эта общая стоимость довольно высока - обычное преобразование fp->int в 10 раз или дороже, чем этот трюк add+store+load.
Однако на x86-64 с плавающей запятой используются инструкции xmm, и стоимость преобразования
fp->int довольно мала, поэтому эта "оптимизация", вероятно, медленнее, чем обычное преобразование.
если это помогает с визуализацией, это магическое значение lua
(2^52+2^51, or base2 of 110 then [50 zeros]
шестнадцатеричный
0x 0018 0000 0000 0000 (18e12)
восьмеричный
0 300 00000 00000 00000 ( 3e17)
Вот более простая реализация вышеупомянутого трюка с Lua:
/**
* Round to the nearest integer.
* for tie-breaks: round half to even (bankers' rounding)
* Only works for inputs in the range: [-2^51, 2^51]
*/
inline double rint(double d)
{
double x = 6755399441055744.0; // 2^51 + 2^52
return d + x - x;
}
Уловка работает для чисел с абсолютным значением < 2 ^ 51.
Это небольшая программа для проверки: ideone.com
#include <cstdio>
int main()
{
// round to nearest integer
printf("%.1f, %.1f\n", rint(-12345678.3), rint(-12345678.9));
// test tie-breaking rule
printf("%.1f, %.1f, %.1f, %.1f\n", rint(-24.5), rint(-23.5), rint(23.5), rint(24.5));
return 0;
}
// output:
// -12345678.0, -12345679.0
// -24.0, -24.0, 24.0, 24.0