Преобразовать двоичную формулу в нормальную форму Шеннона

Question

Я хотел бы знать шаги для преобразования бинарной формулы в нормальную форму Шеннона.

a⪯b⪯c⪯d - variable ordering.
F = b&c&!d|c&d&!b|d&!c|!c&!d

Как я могу преобразовать это в нормальную форму Шеннона?

Answer 1

Вы начинаете с вычисления F|{a=0} и F|{a=1}. Поскольку F не зависит от переменной a, вы получите F для обоих случаев:

F|{a=0} = F
F|{a=1} = F

Вы продолжаете вычислять F|{a=0,b=0}, F|{a=0,b=1}, F|{a=1,b=0} и F|{a=1,b=1}. Ты получишь

F|{a=0,b=0} = F|{a=1,b=0} = c&d|d&!c|!c&!d = !c|d
F|{a=0,b=1} = F|{a=1,b=1} = c&!d|d&!c|!c&!d = !c|!d

Вы продолжаете с переменной c и переменной d и, наконец, получаете:

F = !a(!b(!c(!d&1+d&1)|c(!d&0+d&1))|b(!c(!d&1+d&1)|c(!d&1+d&0))|
     a(!b(!c(!d&1+d&1)|c(!d&0+d&1))|b(!c(!d&1+d&1)|c(!d&1+d&0))

Если вам нужен обратный порядок, просто рассчитайте в обратном порядке переменных, вы можете получить совершенно другой результат.

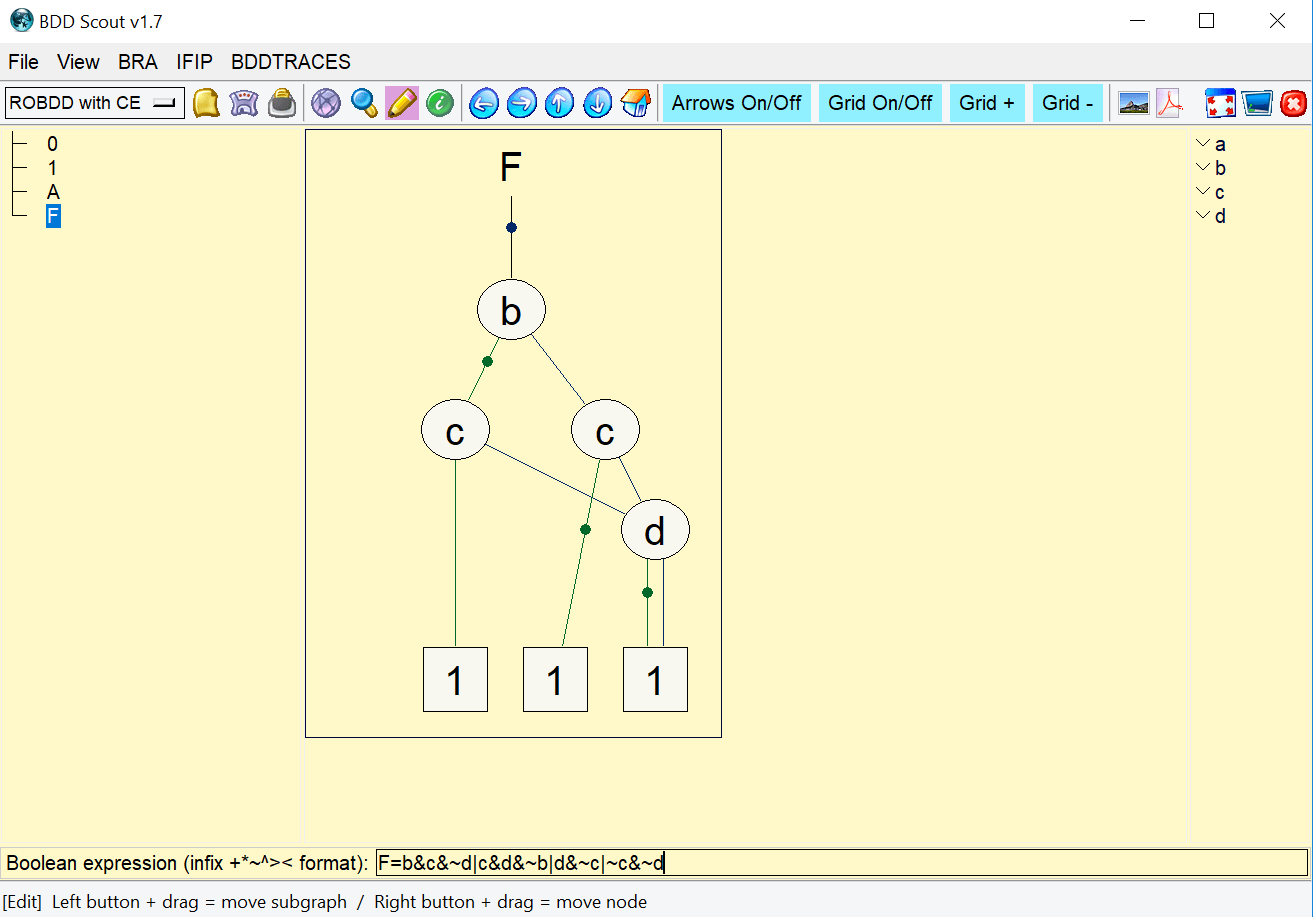
А вот скриншот из BDD Scout ( http://biddy.meolic.com/), к сожалению, этот инструмент пока не поддерживает BDD без дополненных ребер.