Какое значение имеет формула полукластера в статье Google Pregel?
Полукластерный алгоритм упоминается в статье Google Pregel. Оценка полукластера рассчитывается по формуле ниже
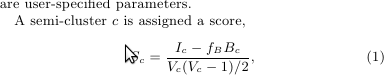
где
Ic - сумма весов всех внутренних ребер
Bc - сумма весов всех граничных ребер
Vc - число вершин в полукластере и
fb - коэффициент оценки граничного края (пользователь определяет от 0 до 1)
Алгоритм был довольно простым, но я не мог понять, как появилась приведенная выше формула. Обратите внимание, что знаменатель - это число ребер, возможных между Vc числом вершин.
Может ли кто-нибудь объяснить это?
2 ответа
Оценка имеет смысл, если вы думаете о количестве, которое она предназначена для сбора.
Проблема, решаемая здесь, состоит в том, чтобы выяснить, как лучше всего расположить вершины графа в полукластеры (просто группу вершин, где каждая вершина может быть в более чем одном полукластере) с некоторой верхней границей общего числа пол-кластер. Таким образом, один из способов найти "лучший" способ - это присвоить оценку любому потенциальному полукластеру (другими словами, любой произвольной группе вершин). Тогда возникает проблема максимизации общего балла.
Итак, полукластер предназначен для захвата кликов в графе. Например, в социальном графе полукластер может быть членом баскетбольной команды средней школы.
Таким образом, больше внутренних краев приравнивается к "лучшему" полукластеру. Это объясняет I_c в числителе. Точно так же вы хотите иметь очень мало граничных ребер, так как если много граничных ребер, то это означает, что, вероятно, будет лучшая полугруппа, содержащая исследуемую вами. Это дает -f_b * B_c в числителе. f_b это просто коэффициент масштабирования, так что вы можете настроить, какой штраф вы хотите назначить граничные края.
Знаменатель также является своего рода масштабным фактором. Он используется для нормализации полукластерных оценок, так что в небольших кластерах не доминируют большие кластеры. Крайним примером этого является, если вы рассмотрите полугруппу всех в мире. Очевидно, что нет никаких краевых границ и тонны внутренних краев, но это, несомненно, менее полезная полугруппа, чем баскетбольная команда средней школы.
Это связано с кликами.
V_c * (V_c - 1) - количество ребер в клике размера V_c.
Таким образом, если вы берете сумму по всем ребрам в группе I_c, это подходящая нормализация для получения среднего арифметического.
Т.е. I_c / (V_c * (V_c - 1)) - средний вес внутри клики.
Теперь термин - f_B * B_c - это штраф за исходящие ребра. ИМХО, он должен быть разделен только на V_c, но это личный вкус, так как я предполагаю, что ожидаемые исходящие ребра будут масштабироваться с количеством членов клики, а не с квадратом этого.