Нахождение пути от начала до конца путем обхода графа
В настоящее время я выполняю школьное задание, в котором мы хотим смоделировать карту автобусного маршрута с использованием графиков (ненаправленных), где края представляют дороги, на которых есть метки, обозначенные буквой автобусного маршрута (на одной дороге может быть автобус a, а на другой может быть автобус). б) и узлы представляют пересечения, тупик или начальные и конечные местоположения. Карта имеет формат прямоугольной / квадратной сетки, поэтому максимальное количество инцидентных ребер, которые может иметь узел, равно 4 (это означает, что к перекрестку подключено 4 дороги).
Я реализовал классы Node, Edge и Graph, а также сумел добавить все ребра и узлы, необходимые для графа, представляющего образец карты. Теперь мне нужно написать метод, который использует Iterator, который хранит все инцидентные ребра узла и целочисленное значение, представляющее, сколько разрешений на изменение шины, и проходит через график, чтобы найти ОДИН путь, который ведет от начального узла к конечный узел без использования большего количества изменений шины, чем указано. Затем верните Итератор, который хранит все узлы, переданные по пути от начала до конца.
Это то, что у меня есть до сих пор для метода (незаконченный, поскольку я застрял):
public Iterator<GraphNode> trip() throws GraphException {
GraphNode startNode = new GraphNode(startLoc); //Creates the starting node.
listOfNodes.add(startNode); //Adds the starting node to the list of nodes that will be the solution.
startNode.setMark(true); //Marks the starting node as true, meaning it has been visited.
pathForEveryNode(graph.incidentEdges(startNode)); //Uses the custom method to find where to go next.
return listOfNodes.iterator(); //Returns the iterator that stores the solution nodes.
}
private List<GraphNode> pathForEveryNode (Iterator<GraphEdge> incidentEdges) throws GraphException {
//This checks if the current node has incident edges or not, if not, then null is returned.
if (incidentEdges == null) {
return null;
} else {
//If the current node does have incident nodes, check the first edge first.
while (incidentEdges.hasNext()) {
tryAgain:{ GraphEdge nextEdge = incidentEdges.next(); //The is the first edge to be checked.
GraphNode endNode = nextEdge.secondEndpoint(); //This is the second end point of the current edge.
/*
* Checks if the current edge and one of the edges connected to the second end point has
* the same bus route set. If not, then the number of changes needs to be checked, if it is,
* then add the second end point to the array list and move to the next set of incident edges.
*/
listOfNodes.add(endNode); //Adds the second end point to the array list.
endNode.setMark(true); //Marks the second end point as true, meaning it has been visited.
tryAgain2:{GraphEdge Snode = graph.incidentEdges(endNode).next();
if (nextEdge.getBusLine() != Snode.getBusLine()) {
/*
* If the number of changes left is larger or equal to 1, it is decreased by 1. Otherwise,
* there is not enough changes left, so back track to the beginning and try the next edge available.
*/
if (kNumOfChanges >= 1) {
kNumOfChanges--;
listOfNodes.add(Snode.secondEndpoint()); //Adds the second end point to the array list.
Snode.secondEndpoint().setMark(true); //Marks the second end point as true, meaning it has been visited.
} else if(kNumOfChanges == 0 && graph.incidentEdges(endNode).hasNext()){ //If the number of changes available or remaining is 0:
break tryAgain2; //Try a different edge connecting to the endNode.
} else if(kNumOfChanges == 0 && !graph.incidentEdges(endNode).hasNext()) {
listOfNodes.remove(endNode); //So the node is removed.
endNode.setMark(false); //Marks the second end point to false, meaning it has not been visited.
break tryAgain; //Try a different incident edge.
}
} else {
listOfNodes.add(Snode.secondEndpoint()); //Adds the second end point to the array list.
Snode.secondEndpoint().setMark(true); //Marks the second end point as true, meaning it has been visited.
}
//If the second end point of the current node is the ending node, return the array list and end the program.
if (Snode.secondEndpoint().getName() == endLoc) {
return listOfNodes;
/*
* If it is not the ending node, check if all of its edges leads to an unmarked node (nodes that has not been visited).
* If there are no nodes that is unmarked (deadend), then this current node doesn't lead any where, so remove it from the
* array list.
*/
} else if (pathForEveryNode(allPathPossibilitiesOneNode(graph.incidentEdges(Snode.secondEndpoint()))) == null) {
listOfNodes.remove(Snode.secondEndpoint()); //remove the current node from the array list.
Snode.secondEndpoint().setMark(false); //Marks the current node to be false, meaning it has not been visited.
listOfNodes.remove(endNode); //So the node is removed.
endNode.setMark(false); //Marks the second end point to false, meaning it has not been visited.
if (kNumOfChanges > 1) {
kNumOfChanges++;
}
}
//Checks if the array list contains the ending node, if it does, then return the array list. Otherwise, return null.
boolean endLocInArray = false;
for(int i = 0; i < listOfNodes.size(); i++) {
if (listOfNodes.get(i).getName() == endLoc) {
endLocInArray = true;
break;
}
}
if(endLocInArray == true) {
return listOfNodes;
}
}}
}
}
return null;
}
и вспомогательный метод, который проверяет, была ли вторая конечная точка уже посещена или нет:
private Iterator<GraphEdge> allPathPossibilitiesOneNode(Iterator<GraphEdge> PossibilitiesIterator) {
List<GraphEdge> allPathPossibilities = new ArrayList<GraphEdge>(); //Initializes the array list that will store the edges.
//This loop goes through all the incident edges connecting to the current node.
while (PossibilitiesIterator.hasNext()) {
GraphEdge currentEdge = PossibilitiesIterator.next(); //The first incident edge.
//This checks if the second end point (next intersection) is marked or not, if not, then add it to the array list.
if (currentEdge.secondEndpoint().getMark() == false) {
allPathPossibilities.add(currentEdge);
}
}
//Return the iterator is the array list is not empty, otherwise return null.
if (!allPathPossibilities.isEmpty()) {
return allPathPossibilities.iterator();
} else {
return null;
}
}
Предполагается сравнить busLine метки ребра, соединенного с первым узлом (firstEndPoint), с ребром, соединенным со вторым узлом первого ребра, чтобы увидеть, совпадают ли автобусные маршруты, если они не совпадают, тогда проверьте, достаточно ли осталось изменений шины.
То, что у меня есть, работает без ошибок, но распечатанное решение - это уже пустой список, хотя так быть не должно.
Мы только начали тему на графиках, и для задания.
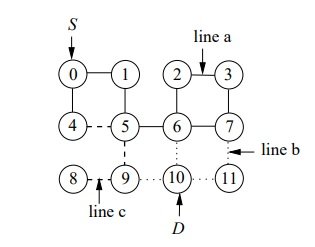
Изменить: пример графика и решения:
Путь для этого маршрута карты составляет 0,1,5,6,10 для узлов, если разрешена 1 смена шины.