Интеграция не удалась в Python QuTiP

Question

Я пытался использовать QuTiP для решения матричного дифференциального уравнения квантовой механики (уравнения Линдблада). Вот код:

from qutip import *
from matplotlib import *
import numpy as np

hamiltonian = np.array([[215, -104.1, 5.1, -4.3  ,4.7,-15.1 ,-7.8 ],
[-104.1,  220.0, 32.6 ,7.1, 5.4, 8.3, 0.8],
      [ 5.1, 32.6, 0.0, -46.8, 1.0 , -8.1, 5.1],
     [-4.3, 7.1, -46.8, 125.0, -70.7, -14.7, -61.5],
       [ 4.7, 5.4, 1.0, -70.7, 450.0, 89.7, -2.5],
    [-15.1, 8.3, -8.1, -14.7, 89.7, 330.0, 32.7],
     [-7.8, 0.8, 5.1, -61.5,  -2.5, 32.7,  280.0]])
H=Qobj(hamiltonian)
ground=Qobj(np.array([[ 0.0863685 ],
  [ 0.17141713],
  [-0.91780802],
  [-0.33999268],
  [-0.04835763],
  [-0.01859027],
  [-0.05006013]]))

rho0 = ground*ground.dag()
from scipy.constants import *
ktuple=physical_constants['Boltzmann constant in eV/K']
k = ktuple[0]* 8065.6
htuple = physical_constants['Planck constant in eV s'] 
hbar = (htuple[0]* 8065.6)/(2*pi)
gamma=(2*pi)*((k*300)/hbar)*(35/(150*hbar))

L1 = Qobj(np.array([[1,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0]]))
L2 = Qobj(np.array([[0,0,0,0,0,0,0],[0,1,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0]]))
L3 = Qobj(np.array([[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,1,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0]]))
L4 = Qobj(np.array([[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,1,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0]]))
L5 = Qobj(np.array([[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,1,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0]]))
L6 = Qobj(np.array([[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,1,0],[0,0,0,0,0,0,0]]))
L7 = Qobj(np.array([[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,1]]))
#Since our gamma variable cannot be directly applied onto the Lindblad operator, we must multiply it with the collapse operators:

L1=gamma*L1
L2=gamma*L2
L3=gamma*L3
L4=gamma*L4
L5=gamma*L5
L6=gamma*L6
L7=gamma*L7

options = Options(nsteps=100000)

results = mesolve(H, rho0, np.linspace(0.0, 1000, 20),[L1,L2,L3,L4,L5,L6,L7],[],options=options)
print results

Этот код должен решить следующее уравнение:

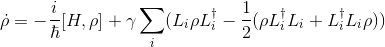
где L_i - матрицы (в списке: [L1,L2,L3,L4,L5,L6,L7]), H - гамильтониан, другая матрица, 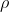матрица плотности, и 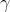постоянная, равная 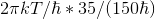где T - температура, k - постоянная Больцмана, и 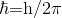где h - постоянная Планка.

Каждый раз, когда я запускаю код, он выдает мне следующую ошибку:

ZVODE--  At T (=R1) and step size H (=R2), the
       corrector convergence failed repeatedly
       or with abs(H) = HMIN
      In above,  R1 =  0.0000000000000D+00   R2 =  0.1202322246215D-36
/usr/local/lib/python2.7/dist-packages/scipy/integrate/_ode.py:853: UserWarning: zvode: Repeated convergence failures. (Perhaps bad Jacobian supplied or wrong choice of MF o
r tolerances.)
  'Unexpected istate=%s' % istate))
Traceback (most recent call last):
  File "lindbladqutip.py", line 48, in <module>
    results = mesolve(H, rho0, np.linspace(0.0, 1000, 20),[L1,L2,L3,L4,L5,L6,L7],[],options=options)
  File "/projects/d6138712-e5f4-4d85-9d4d-77ce0a7b4a61/.local/lib/python2.7/site-packages/qutip/mesolve.py", line 264, in mesolve
    progress_bar)
  File "/projects/d6138712-e5f4-4d85-9d4d-77ce0a7b4a61/.local/lib/python2.7/site-packages/qutip/mesolve.py", line 692, in _mesolve_const
    return _generic_ode_solve(r, rho0, tlist, e_ops, opt, progress_bar)
  File "/projects/d6138712-e5f4-4d85-9d4d-77ce0a7b4a61/.local/lib/python2.7/site-packages/qutip/mesolve.py", line 866, in _generic_ode_solve
    raise Exception("ODE integration error: Try to increase "
Exception: ODE integration error: Try to increase the allowed number of substeps by increasing the nsteps parameter in the Options class.

После некоторого отладочного анализа кажется, что первая или вторая интеграция не удалась. Ошибка говорит мне увеличить параметр nsteps, который я пробовал. Даже тогда это терпит неудачу. Изменение списка раз (функция np.linspace создает список раз) также не имеет никакого эффекта.

Я отчаянно хочу знать, что я могу сделать, чтобы исправить эту ошибку. Пожалуйста, прокомментируйте, если вам всем нужно больше деталей.

Спасибо за вашу помощь!

Answer 1

С точки зрения программирования, проблема заключается в вашей ценности gamma и, следовательно, размер ваших операторов коллапса. Распечатывать gamma - это порядка 10**25 - это, кажется, то, что препятствует тому, чтобы решатель сходился.

Просто для тестирования (я инженер, а не квантовый физик...), я поместил меньшее значение gamma (например, 0,1), решатель, кажется, работает и дает, по-видимому, разумный вывод в results.states

Я не совсем понимаю вашу gamma - кажется, что у вас есть единицы измерения см^-1 с^-2, как вы его настроили. Интересно, если вы хотите разделить только на hbar однажды, может быть. Как я уже сказал, я не квантовый физик, поэтому я только догадываюсь здесь, основываясь на том, что заставляет программирование зависеть в сочетании с небольшим анализом измерений.

РЕДАКТИРОВАТЬ

OP указывает в комментариях, что неправильный порядок величины / единиц для gamma похоже, это проблема программирования (то есть предотвращение схождения числового исчисления), но не совсем ясно, как рассчитать гамму. На данном этапе, возможно, стоит опубликовать вопрос на http://physics.stackexchange.com/ или http://math.stackexchange.com/ об этом - если нужно, сослаться на этот вопрос для контекста.

РЕДАКТИРОВАТЬ 2

Отмечу, что вы задали этот связанный вопрос на сайте физики. Это проясняет, откуда взято выражение для гаммы, и тем самым проясняет, что константные термины представлены просто 30 а также 150 в этом вопросе фактически есть единицы (энергия и частота соответственно). Это меняет размерный анализ - единицами гаммы являются s^-1 или, при соответствующем преобразовании, см^-1.

Это также показывает значение, которое вы упоминаете в комментариях - 300 см^-1.