Как рассчитать евклидово расстояние с помощью NumPy?
У меня есть две точки в 3D:
(xa, ya, za)
(xb, yb, zb)
И я хочу рассчитать расстояние:
dist = sqrt((xa-xb)^2 + (ya-yb)^2 + (za-zb)^2)
Какой лучший способ сделать это с NumPy или с Python в целом? Я имею:
a = numpy.array((xa ,ya, za))
b = numpy.array((xb, yb, zb))
27 ответов
Использование numpy.linalg.norm:
dist = numpy.linalg.norm(a-b)
Для этого есть функция в SciPy. Это называется евклидово.
Пример:
from scipy.spatial import distance
a = (1, 2, 3)
b = (4, 5, 6)
dst = distance.euclidean(a, b)
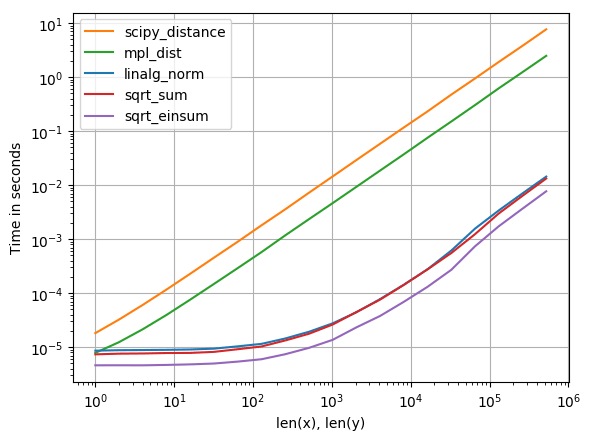
Для тех, кто заинтересован в одновременном вычислении нескольких расстояний, я провел небольшое сравнение с использованием perfplot (небольшой мой проект). Оказывается, что
a_min_b = a - b
numpy.sqrt(numpy.einsum('ij,ij->i', a_min_b, a_min_b))
вычисляет расстояния строк в a а также b быстрый. Это действительно справедливо только для одного ряда!
Код для воспроизведения сюжета:
import matplotlib
import numpy
import perfplot
from scipy.spatial import distance
def linalg_norm(data):
a, b = data
return numpy.linalg.norm(a-b, axis=1)
def sqrt_sum(data):
a, b = data
return numpy.sqrt(numpy.sum((a-b)**2, axis=1))
def scipy_distance(data):
a, b = data
return list(map(distance.euclidean, a, b))
def mpl_dist(data):
a, b = data
return list(map(matplotlib.mlab.dist, a, b))
def sqrt_einsum(data):
a, b = data
a_min_b = a - b
return numpy.sqrt(numpy.einsum('ij,ij->i', a_min_b, a_min_b))
perfplot.show(
setup=lambda n: numpy.random.rand(2, n, 3),
n_range=[2**k for k in range(20)],
kernels=[linalg_norm, scipy_distance, mpl_dist, sqrt_sum, sqrt_einsum],
logx=True,
logy=True,
xlabel='len(x), len(y)'
)
Я хочу изложить простой ответ с различными заметками о производительности. np.linalg.norm сделает, возможно, больше, чем вам нужно:
dist = numpy.linalg.norm(a-b)
Во-первых, эта функция предназначена для работы со списком и возврата всех значений, например, для сравнения расстояния от pA к набору баллов sP:
sP = set(points)
pA = point
distances = np.linalg.norm(sP - pA, ord=2, axis=1.) # 'distances' is a list
Помните несколько вещей:
- Вызовы функций Python стоят дорого.
- [Обычный] Python не кэширует поиск имен.
Так
def distance(pointA, pointB):
dist = np.linalg.norm(pointA - pointB)
return dist
не так невинно, как кажется.
>>> dis.dis(distance)
2 0 LOAD_GLOBAL 0 (np)
2 LOAD_ATTR 1 (linalg)
4 LOAD_ATTR 2 (norm)
6 LOAD_FAST 0 (pointA)
8 LOAD_FAST 1 (pointB)
10 BINARY_SUBTRACT
12 CALL_FUNCTION 1
14 STORE_FAST 2 (dist)
3 16 LOAD_FAST 2 (dist)
18 RETURN_VALUE
Во-первых - каждый раз, когда мы вызываем его, мы должны выполнить глобальный поиск для "np", поиск в области видимости для "linalg" и поиск в области видимости для "нормы", а издержки простого вызова функции могут приравняться к десяткам Python инструкции.
Наконец, мы потратили две операции, чтобы сохранить результат и перезагрузить его для возврата...
Первый шаг к улучшению: сделайте поиск быстрее, пропустите магазин
def distance(pointA, pointB, _norm=np.linalg.norm):
return _norm(pointA - pointB)
Мы получаем гораздо более упорядоченный:
>>> dis.dis(distance)
2 0 LOAD_FAST 2 (_norm)
2 LOAD_FAST 0 (pointA)
4 LOAD_FAST 1 (pointB)
6 BINARY_SUBTRACT
8 CALL_FUNCTION 1
10 RETURN_VALUE
Затраты на вызов функции по-прежнему составляют некоторую работу. И вы захотите сделать тесты, чтобы определить, лучше ли вам делать математику самостоятельно:
def distance(pointX, pointY):
return (
((pointX.x - pointY.x) ** 2) +
((pointX.y - pointY.y) ** 2) +
((pointX.z - pointY.z) ** 2)
) ** 0.5 # fast sqrt
На некоторых платформах **0.5 быстрее чем math.sqrt, Ваш пробег может отличаться.
**** Расширенные заметки производительности.
Почему вы рассчитываете расстояние? Если единственной целью является его отображение,
print("The target is %.2fm away" % (distance(a, b)))
двигаться вперед. Но если вы сравниваете расстояния, проводите проверки дальности и т. Д., Я хотел бы добавить некоторые полезные наблюдения за производительностью.
Давайте рассмотрим два случая: сортировка по расстоянию или отбор списка по элементам, которые соответствуют ограничению диапазона.
# Ultra naive implementations. Hold onto your hat.
def sort_things_by_distance(origin, things):
return things.sort(key=lambda thing: distance(origin, thing))
def in_range(origin, range, things):
things_in_range = []
for thing in things:
if distance(origin, thing) <= range:
things_in_range.append(thing)
Первое, что нам нужно помнить, это то, что мы используем Пифагор для вычисления расстояния (dist = sqrt(x^2 + y^2 + z^2)) поэтому мы делаем много sqrt звонки. Математика 101:
dist = root ( x^2 + y^2 + z^2 )
:.
dist^2 = x^2 + y^2 + z^2
and
sq(N) < sq(M) iff M > N
and
sq(N) > sq(M) iff N > M
and
sq(N) = sq(M) iff N == M
Вкратце: пока нам не потребуется расстояние в единице X, а не X^2, мы можем исключить самую сложную часть вычислений.
# Still naive, but much faster.
def distance_sq(left, right):
""" Returns the square of the distance between left and right. """
return (
((left.x - right.x) ** 2) +
((left.y - right.y) ** 2) +
((left.z - right.z) ** 2)
)
def sort_things_by_distance(origin, things):
return things.sort(key=lambda thing: distance_sq(origin, thing))
def in_range(origin, range, things):
things_in_range = []
# Remember that sqrt(N)**2 == N, so if we square
# range, we don't need to root the distances.
range_sq = range**2
for thing in things:
if distance_sq(origin, thing) <= range_sq:
things_in_range.append(thing)
Отлично, обе функции больше не делают никаких дорогих квадратных корней. Это будет намного быстрее. Мы также можем улучшить in_range, преобразовав его в генератор:
def in_range(origin, range, things):
range_sq = range**2
yield from (thing for thing in things
if distance_sq(origin, thing) <= range_sq)
Это особенно полезно, если вы делаете что-то вроде:
if any(in_range(origin, max_dist, things)):
...
Но если следующая вещь, которую вы собираетесь сделать, требует расстояния,
for nearby in in_range(origin, walking_distance, hotdog_stands):
print("%s %.2fm" % (nearby.name, distance(origin, nearby)))
рассмотреть возможность получения кортежей:
def in_range_with_dist_sq(origin, range, things):
range_sq = range**2
for thing in things:
dist_sq = distance_sq(origin, thing)
if dist_sq <= range_sq: yield (thing, dist_sq)
Это может быть особенно полезно, если вы можете связать проверки диапазона ("найдите вещи, которые находятся около X и в пределах Nm от Y", так как вам не нужно снова вычислять расстояние).
Но что, если мы ищем действительно большой список things и мы ожидаем, что многие из них не заслуживают рассмотрения?
На самом деле есть очень простая оптимизация:
def in_range_all_the_things(origin, range, things):
range_sq = range**2
for thing in things:
dist_sq = (origin.x - thing.x) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.y - thing.y) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.z - thing.z) ** 2
if dist_sq <= range_sq:
yield thing
Будет ли это полезно, будет зависеть от размера "вещей".
def in_range_all_the_things(origin, range, things):
range_sq = range**2
if len(things) >= 4096:
for thing in things:
dist_sq = (origin.x - thing.x) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.y - thing.y) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.z - thing.z) ** 2
if dist_sq <= range_sq:
yield thing
elif len(things) > 32:
for things in things:
dist_sq = (origin.x - thing.x) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.y - thing.y) ** 2 + (origin.z - thing.z) ** 2
if dist_sq <= range_sq:
yield thing
else:
... just calculate distance and range-check it ...
И снова, подумайте о выдаче dist_sq. Наш пример хот-дога становится:
# Chaining generators
info = in_range_with_dist_sq(origin, walking_distance, hotdog_stands)
info = (stand, dist_sq**0.5 for stand, dist_sq in info)
for stand, dist in info:
print("%s %.2fm" % (stand, dist))
Еще один пример этого метода решения проблем:
def dist(x,y):
return numpy.sqrt(numpy.sum((x-y)**2))
a = numpy.array((xa,ya,za))
b = numpy.array((xb,yb,zb))
dist_a_b = dist(a,b)
Начало Python 3.8, math модуль напрямую обеспечивает dist функция, которая возвращает евклидово расстояние между двумя точками (задается как кортеж координат):
from python import math
dist((1, 2, 6), (-2, 3, 2)) # 5.0990195135927845
Если вы работаете со списками вместо кортежей:
dist(tuple([1, 2, 6]), tuple([-2, 3, 2]))
Это можно сделать следующим образом. Я не знаю, как это быстро, но он не использует NumPy.
from math import sqrt
a = (1, 2, 3) # Data point 1
b = (4, 5, 6) # Data point 2
print sqrt(sum( (a - b)**2 for a, b in zip(a, b)))
Хороший однострочник:
dist = numpy.linalg.norm(a-b)
Однако, если скорость вызывает беспокойство, я бы порекомендовал поэкспериментировать на вашей машине. Я обнаружил, что с помощью math библиотеки sqrt с ** Оператор для квадрата намного быстрее на моей машине, чем однолинейное решение NumPy.
Я провел свои тесты с помощью этой простой программы:
#!/usr/bin/python
import math
import numpy
from random import uniform
def fastest_calc_dist(p1,p2):
return math.sqrt((p2[0] - p1[0]) ** 2 +
(p2[1] - p1[1]) ** 2 +
(p2[2] - p1[2]) ** 2)
def math_calc_dist(p1,p2):
return math.sqrt(math.pow((p2[0] - p1[0]), 2) +
math.pow((p2[1] - p1[1]), 2) +
math.pow((p2[2] - p1[2]), 2))
def numpy_calc_dist(p1,p2):
return numpy.linalg.norm(numpy.array(p1)-numpy.array(p2))
TOTAL_LOCATIONS = 1000
p1 = dict()
p2 = dict()
for i in range(0, TOTAL_LOCATIONS):
p1[i] = (uniform(0,1000),uniform(0,1000),uniform(0,1000))
p2[i] = (uniform(0,1000),uniform(0,1000),uniform(0,1000))
total_dist = 0
for i in range(0, TOTAL_LOCATIONS):
for j in range(0, TOTAL_LOCATIONS):
dist = fastest_calc_dist(p1[i], p2[j]) #change this line for testing
total_dist += dist
print total_dist
На моей машине math_calc_dist работает намного быстрее чем numpy_calc_dist: 1,5 секунды против 23,5 секунды.
Чтобы измерить разницу между fastest_calc_dist а также math_calc_dist Я должен был TOTAL_LOCATIONS до 6000. Тогда fastest_calc_dist занимает ~50 секунд, пока math_calc_dist занимает ~60 секунд.
Вы также можете поэкспериментировать с numpy.sqrt а также numpy.square хотя оба были медленнее, чем math альтернативы на моей машине.
Мои тесты были запущены с Python 2.6.6.
Вы можете просто вычесть векторы и затем получить внутренний продукт.
Следуя вашему примеру,
a = numpy.array((xa, ya, za))
b = numpy.array((xb, yb, zb))
tmp = a - b
sum_squared = numpy.dot(tmp.T, tmp)
result sqrt(sum_squared)
Это простой код и его легко понять.
Я нахожу функцию dist в matplotlib.mlab, но не думаю, что она достаточно удобна.
Я публикую это здесь только для справки.
import numpy as np
import matplotlib as plt
a = np.array([1, 2, 3])
b = np.array([2, 3, 4])
# Distance between a and b
dis = plt.mlab.dist(a, b)
Мне нравится np.dot (точка продукта):
a = numpy.array((xa,ya,za))
b = numpy.array((xb,yb,zb))
distance = (np.dot(a-b,a-b))**.5
Начиная с Python 3.8
Начиная с Python 3.8 math модуль включает функцию math.dist().
См. Здесь https://docs.python.org/3.8/library/math.html.
math.dist (p1, p2)
Возвращает евклидово расстояние между двумя точками p1 и p2, каждая из которых задана как последовательность (или итерация) координат.
import math
print( math.dist( (0,0), (1,1) )) # sqrt(2) -> 1.4142
print( math.dist( (0,0,0), (1,1,1) )) # sqrt(3) -> 1.7321
С Python 3.8 это очень просто.
https://docs.python.org/3/library/math.html
math.dist(p, q)
Верните евклидово расстояние между двумя точками p и q, каждая из которых задана как последовательность (или итерация) координат. Две точки должны иметь одинаковый размер.
Примерно эквивалентно:
sqrt(sum((px - qx) ** 2.0 for px, qx in zip(p, q)))
Имеющий a а также b как вы их определили, вы также можете использовать:
distance = np.sqrt(np.sum((a-b)**2))
Вот краткий код евклидова расстояния в Python с учетом двух точек, представленных в виде списков в Python.
def distance(v1,v2):
return sum([(x-y)**2 for (x,y) in zip(v1,v2)])**(0.5)
Рассчитаем евклидово расстояние для многомерного пространства:
import math
x = [1, 2, 6]
y = [-2, 3, 2]
dist = math.sqrt(sum([(xi-yi)**2 for xi,yi in zip(x, y)]))
5.0990195135927845
import math
dist = math.hypot(math.hypot(xa-xb, ya-yb), za-zb)
import numpy as np
# any two python array as two points
a = [0, 0]
b = [3, 4]
Сначала вы меняете список на массив numpy и делаете так:print(np.linalg.norm(np.array(a) - np.array(b))). Второй метод прямо из списка Python:print(np.linalg.norm(np.subtract(a,b)))
import numpy as np
from scipy.spatial import distance
input_arr = np.array([[0,3,0],[2,0,0],[0,1,3],[0,1,2],[-1,0,1],[1,1,1]])
test_case = np.array([0,0,0])
dst=[]
for i in range(0,6):
temp = distance.euclidean(test_case,input_arr[i])
dst.append(temp)
print(dst)
Если вы хотите что-то более явное, вы можете легко написать формулу следующим образом:
np.sqrt(np.sum((a-b)**2))
Даже с массивами из 10_000_000 элементов на моей машине это все еще выполняется за 0,1 с.
Вы можете легко использовать формулу
distance = np.sqrt(np.sum(np.square(a-b)))
что на самом деле не более чем использование теоремы Пифагора для вычисления расстояния путем сложения квадратов Δx, Δy и Δz и укоренения результата.
Другие ответы работают для чисел с плавающей запятой, но неправильно вычисляют расстояние для целочисленных dtypes, которые подвержены переполнению и потере значимости. Обратите внимание, что дажеscipy.distance.euclidean есть эта проблема:
>>> a1 = np.array([1], dtype='uint8')
>>> a2 = np.array([2], dtype='uint8')
>>> a1 - a2
array([255], dtype=uint8)
>>> np.linalg.norm(a1 - a2)
255.0
>>> from scipy.spatial import distance
>>> distance.euclidean(a1, a2)
255.0
Это обычное дело, поскольку многие библиотеки изображений представляют изображение как ndarray с dtype="uint8". Это означает, что если у вас светло-серое изображение (скажем, все пиксели имеют цвет#010101) и вы сравниваете его с черным изображением, вы можете получить x-y состоящий из 255во всех ячейках, что регистрируется как два изображения, находящиеся очень далеко друг от друга. Для беззнаковых целочисленных типов (например, uint8) вы можете безопасно вычислить расстояние в numpy как:
np.linalg.norm(np.maximum(x, y) - np.minimum(x, y))
Для целочисленных типов со знаком вы можете сначала привести к float:
np.linalg.norm(x.astype("float") - y.astype("float"))
В частности, для данных изображения вы можете использовать метод нормы opencv:
import cv2
cv2.norm(x, y, cv2.NORM_L2)
Как лучше всего сделать это с помощью NumPy или Python в целом? У меня есть:
Ну, лучший способ был бы самым безопасным, а также самым быстрым
Я бы предложил использовать гипотезу для получения надежных результатов, поскольку вероятность недостаточного и переполнения очень мала по сравнению с написанием собственного калькулятора sqroot.
Давайте посмотрим math.hypot, np.hypot vs vanilla
np.sqrt(np.sum((np.array([i, j, k])) ** 2, axis=1))
i, j, k = 1e+200, 1e+200, 1e+200
math.hypot(i, j, k)
# 1.7320508075688773e+200
np.sqrt(np.sum((np.array([i, j, k])) ** 2))
# RuntimeWarning: overflow encountered in square
Скорость мудрая математика. Гипотеза выглядит лучше
%%timeit
math.hypot(i, j, k)
# 100 ns ± 1.05 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)
%%timeit
np.sqrt(np.sum((np.array([i, j, k])) ** 2))
# 6.41 µs ± 33.3 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
Самое быстрое решение, которое я мог придумать для большого количества расстояний, — это использование numexpr. На моей машине это быстрее, чем использование numpy einsum:
import numexpr as ne
import numpy as np
np.sqrt(ne.evaluate("sum((a_min_b)**2,axis=1)"))
1. Векторизация SciPy для евклидовой матрицы расстояний.
Тесты @Nico Schlömer показывают scipyeuclidean()функция будет намного медленнее, чем ее коллеги. Причина в том, что он предназначен для работы с парой точек, а не с массивом точек; таким образом, не векторизовано. Кроме того, его тест использует код для определения евклидовых расстояний между массивами одинаковой длины.
Если вам нужно вычислить евклидову матрицу расстояний между каждой парой точек из двух наборов входных данных, есть еще одна функция SciPy, которая работает намного быстрее, чем numpy.
Рассмотрим следующий пример, где содержит 3 точки и содержит 2 точки. SciPy вычисляет евклидовы расстояния между каждой точкой вaв каждую точку вb, поэтому в этом примере будет возвращена матрица 3x2.
import numpy as np
from scipy.spatial import distance
a = [(1, 2, 3), (3, 4, 5), (2, 3, 6)]
b = [(1, 2, 3), (4, 5, 6)]
dsts1 = distance.cdist(a, b)
# array([[0. , 5.19615242],
# [3.46410162, 1.73205081],
# [3.31662479, 2.82842712]])
Это особенно полезно, если у нас есть набор точек и мы хотим найти ближайшее расстояние к каждой точке, кроме самой себя; общий вариант использования — обработка естественного языка. Например, чтобы вычислить евклидовы расстояния между каждой парой точек в коллекции,distance.cdist(a, a)делает свою работу. Поскольку расстояние от точки до самой себя равно 0, все диагонали этой матрицы будут равны нулю.
Ту же задачу можно выполнить с помощью методов, использующих только numpy, используя широковещательную рассылку. Нам просто нужно добавить еще одно измерение в один из массивов.
# using `linalg.norm`
dsts2 = np.linalg.norm(np.array(a)[:, None] - b, axis=-1)
# using a `sqrt` + `sum` + `square`
dsts3 = np.sqrt(np.sum((np.array(a)[:, None] - b)**2, axis=-1))
# equality check
np.allclose(dsts1, dsts2) and np.allclose(dsts1, dsts3) # True
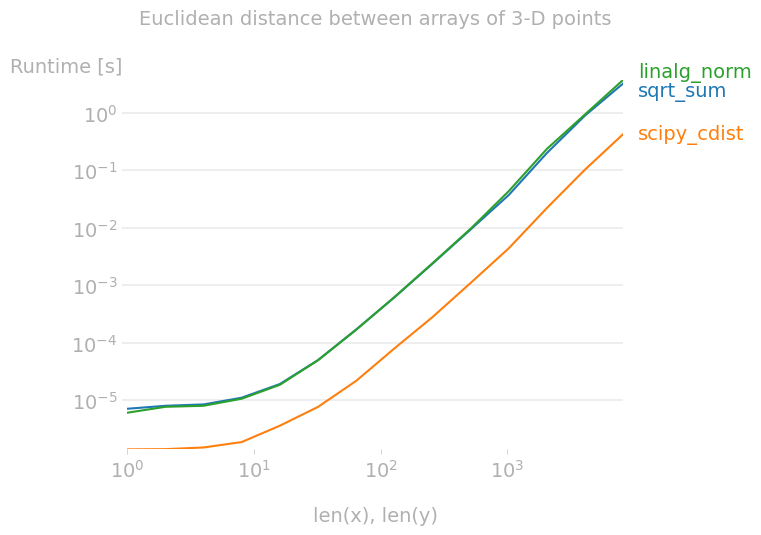
Как упоминалось ранее,cdist()намного быстрее, чем numpy-аналоги. Следующий график показывает то же самое.1
2. Scikit-learn
Scikit-learn — довольно большая библиотека, поэтому, если вы не используете ее для чего-то другого, нет особого смысла импортировать ее только для расчета евклидова расстояния, но для полноты она также имеетeuclidean_distances(),paired_distances()иpairwise_distances()методы, которые можно использовать для вычисления евклидовых расстояний. У него есть и другие удобные методы вычисления парных расстояний, которые стоит проверить.
Одна полезная вещь в методах scikit-learn заключается в том, что они могут обрабатывать разреженные матрицы как есть, тогда как scipy/numpy потребуется преобразовать разреженные матрицы в массивы для выполнения вычислений, поэтому в зависимости от размера данных методы scikit-learn могут быть единственная функция, которая работает.
Пример:
from scipy import sparse
from sklearn.metrics import pairwise
A = sparse.random(1_000_000, 3)
b = [(1, 2, 3), (4, 5, 6)]
dsts = pairwise.euclidean_distances(A, b)
1 Код, используемый для создания графика производительности:
import numpy as np
from scipy.spatial import distance
import perfplot
import matplotlib.pyplot as plt
def sqrt_sum(arr):
return np.sqrt(np.sum((arr[:, None] - arr) ** 2, axis=-1))
def linalg_norm(arr):
return np.linalg.norm(arr[:, None] - arr, axis=-1)
def scipy_cdist(arr):
return distance.cdist(arr, arr)
perfplot.plot(
setup=lambda n: np.random.rand(n, 3),
n_range=[2 ** k for k in range(14)],
kernels=[sqrt_sum, scipy_cdist, linalg_norm],
title="Euclidean distance between arrays of 3-D points",
xlabel="len(x), len(y)",
equality_check=np.allclose
);
Сначала найдите разницу двух матриц. Затем примените поэлементное умножение с помощью команды умножения numpy. После этого найдите суммирование умноженной на элемент новой матрицы. Наконец, найдите квадратный корень суммирования.
def findEuclideanDistance(a, b):
euclidean_distance = a - b
euclidean_distance = np.sum(np.multiply(euclidean_distance, euclidean_distance))
euclidean_distance = np.sqrt(euclidean_distance)
return euclidean_distance
Если вы хотите найти расстояние от конкретной точки до первого из сокращений, которые вы можете использовать, плюс вы можете сделать это с любым количеством измерений.
import numpy as np
A = [3,4]
Dis = np.sqrt(A[0]**2 + A[1]**2)