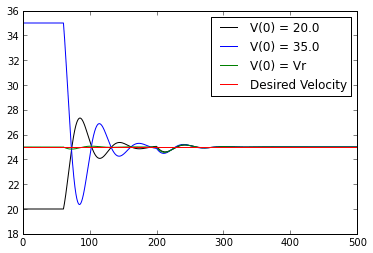
Интегральная система управления не ведет себя должным образом

Question

Вчера я разместил здесь вопрос: ValueError и odepack.error с использованием integrate.odeint(), на который, как мне показалось, был успешно получен ответ. Однако с тех пор я заметил несколько вещей.

1. При запуске этой программы она не стремится к желаемой скорости vr
2. При запуске программы и изменении угла (представляющего уклон дороги) по мере изменения времени она не всегда возвращается к желаемой скорости vr или даже к предыдущему устойчивому состоянию.

Эта программа предназначена для моделирования встроенной системы управления (в частности, круиз-контроля). В настоящее время он начинается со скорости v0, работает с этой скоростью в течение некоторого времени, а затем включается круиз-контроль. В этот момент мы должны увидеть изменение скорости (мы это делаем), которое в конечном итоге стабилизируется на желаемой скорости vr. Это не так. Это достигает некоторого другого значения по неизвестным причинам, и это значение отличается в зависимости от градиента катания. Независимо от начальной скорости он все еще не может достичь желаемой скорости

Я играл с различными параметрами и переменными безрезультатно. Я думаю, что проблема в том, что контроллер не передает правильную текущую скорость, однако я не уверен, как решить эту проблему.

Если вам нужна дополнительная информация, дайте мне знать. Если я должен был отредактировать предыдущий вопрос, просто дайте мне знать, и я сделаю это вместо этого, извините заранее.

Вот мой код:

import matplotlib.pylab as plt
import numpy as np
import scipy.integrate as integrate

##Parameters
kp = .5 #proportional gain
ki = .1 #integral gain
vr = 25 #desired velocity in m/s
Tm = 190 #Max Torque in Nm
wm = 420 #engine speed
B = 0.4 #Beta
an = 12 #at gear 4
p = 1.3 #air density
Cd = 0.32 #Drag coefficient
Cr = .01 #Coefficient of rolling friction
A = 2.4 #frontal area

##Variables
m = 18000.0 #weight
v0 = 20. #starting velocity
t = np.linspace(61, 500, 5000) #time
theta = np.radians(4) #Theta

def torque(v):    
    return Tm * (1 - B*(an*v/wm - 1)**2)  

def vderivs(v, t):
    v1 = an * controller(v, t) * torque(v)
    v2 = m*Cr*np.sign(v)
    v3 = 0.5*p*Cd*A*v**2
    v4 = m*np.sin(theta)
    vtot = v1-v2-v3-v4*(t>=200)
    return vtot/m

def uderivs(v, t):
    return vr - v

def controller(currentV, time):
    z = integrate.odeint(uderivs, currentV, time)
    return kp*(vr-currentV) + ki*z.squeeze()

def velocity(desired, theta, time):
    return integrate.odeint(vderivs, desired, time)

t0l = [i for i in range(61)]
vf=[v0 for i in range(61)]+[v for v in velocity(v0,theta,t)]
tf=t0l+[time for time in t]

plt.plot(tf, vf, 'k-', label=('V(0) = '+str(v0)))

v0=35.
vf=[v0 for i in range(61)]+[v for v in velocity(v0,theta,t)]
plt.plot(tf, vf, 'b-', label=('V(0) = '+str(v0)))

v0=vr
vf=[v0 for i in range(61)]+[v for v in velocity(v0,theta,t)]
plt.plot(tf, vf, 'g-', label=('V(0) = Vr'))

plt.axhline(y=vr, xmin=0, xmax=1000, color='r', label='Desired Velocity')
plt.legend(loc = "upper right")
plt.axis([0,500,18,36])
plt.show()

Это то, что изображено при запуске программы как есть, с использованием диапазона начальных скоростей

Первое резкое изменение скорости происходит, когда запускается круиз-контроль, а второе - когда изменяется градиент движения.

Answer 1

Ваше предположение верно. Целевая система и ПИ-контроллер интегрированы, вы не можете разделить его на две части. Я изменил ваш код, чтобы система имела две переменные состояния: одну для скорости системы, другую для интегрирования ошибки управления:

import matplotlib.pylab as plt
import numpy as np
import scipy.integrate as integrate

##Parameters
kp = .5 #proportional gain
ki = .1 #integral gain
vr = 25 #desired velocity in m/s
Tm = 190 #Max Torque in Nm
wm = 420 #engine speed
B = 0.4 #Beta
an = 12 #at gear 4
p = 1.3 #air density
Cd = 0.32 #Drag coefficient
Cr = .01 #Coefficient of rolling friction
A = 2.4 #frontal area

##Variables
m = 18000.0 #weight
v0 = 20. #starting velocity
t = np.linspace(61, 500, 5000) #time
theta = np.radians(4) #Theta

def torque(v):    
    return Tm * (1 - B*(an*v/wm - 1)**2)  

def vderivs(status, t):
    v, int_err = status

    err = vr - v
    control = kp * err + ki * int_err

    v1 = an * control * torque(v)
    v2 = m*Cr*np.sign(v)
    v3 = 0.5*p*Cd*A*v**2
    v4 = m*np.sin(theta)
    vtot = v1-v2-v3-v4*(t>=200)
    return vtot/m, err

def velocity(desired, theta, time):
    return integrate.odeint(vderivs, [desired, 0], time)[:, 0]

t0l = [i for i in range(61)]
vf=[v0 for i in range(61)]+[v for v in velocity(v0,theta,t)]
tf=t0l+[time for time in t]

plt.plot(tf, vf, 'k-', label=('V(0) = '+str(v0)))

v0=35.
vf=[v0 for i in range(61)]+[v for v in velocity(v0,theta,t)]
plt.plot(tf, vf, 'b-', label=('V(0) = '+str(v0)))

v0=vr
vf=[v0 for i in range(61)]+[v for v in velocity(v0,theta,t)]
plt.plot(tf, vf, 'g-', label=('V(0) = Vr'))

plt.axhline(y=vr, xmin=0, xmax=1000, color='r', label='Desired Velocity')
plt.legend(loc = "upper right")
plt.axis([0,500,18,36])
plt.show()

выход: