Роль предвзятости в нейронных сетях
Я знаю о градиентном спуске и теореме обратного распространения. Чего я не понимаю: когда важно использовать предвзятость и как вы ее используете?
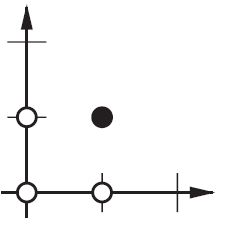
Например, при отображении AND Функция, когда я использую 2 входа и 1 выход, он не дает правильные веса, однако, когда я использую 3 входа (1 из которых является смещением), он дает правильные веса.
18 ответов
Я думаю, что предубеждения почти всегда полезны. По сути, значение смещения позволяет вам смещать функцию активации влево или вправо, что может иметь решающее значение для успешного обучения.
Это может помочь взглянуть на простой пример. Рассмотрим эту сеть с 1 входом и 1 выходом, которая не имеет смещения:
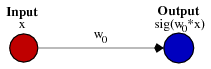
Выход сети вычисляется путем умножения входных данных (x) на вес (w0) и передачи результата через некоторую функцию активации (например, сигмовидную функцию).
Вот функция, которую эта сеть вычисляет для различных значений w0:
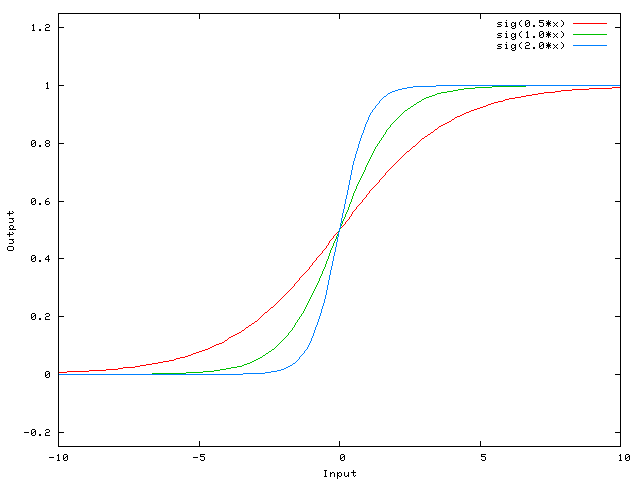
Изменение веса w0 существенно меняет "крутизну" сигмовидной кишки. Это полезно, но что если вы хотите, чтобы сеть выводила 0, когда х равен 2? Простое изменение крутизны сигмоида не сработает - вы хотите иметь возможность сдвигать всю кривую вправо.
Это именно то, что позволяет сделать уклон. Если мы добавим смещение в эту сеть, вот так:
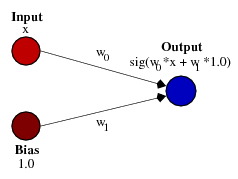
... тогда выходной сигнал сети становится sig (w0* x + w1* 1.0). Вот как выглядит выход сети для различных значений w1:
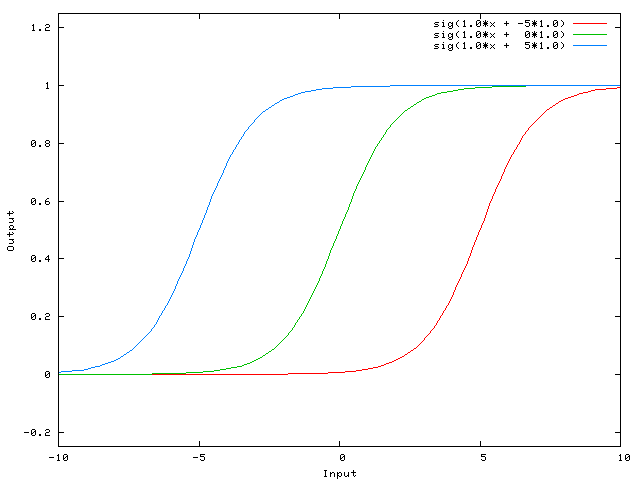
При весе -5 для w1 кривая сдвигается вправо, что позволяет нам иметь сеть, которая выводит 0, когда x равен 2.
Просто чтобы добавить мои два цента.
Более простой способ понять, что такое смещение: оно чем-то похоже на константу b линейной функции
у = топор + б
Это позволяет вам перемещать линию вверх и вниз, чтобы лучше соответствовать прогнозу с данными. Без b линия всегда проходит через начало координат (0, 0), и вы можете получить худшее соответствие.
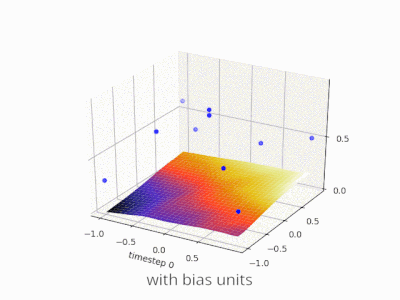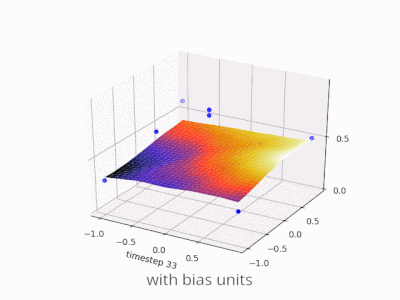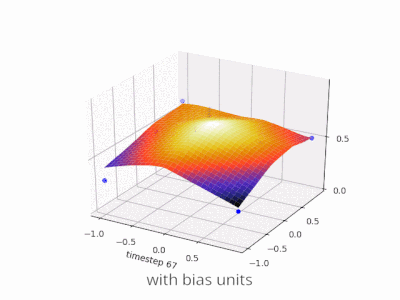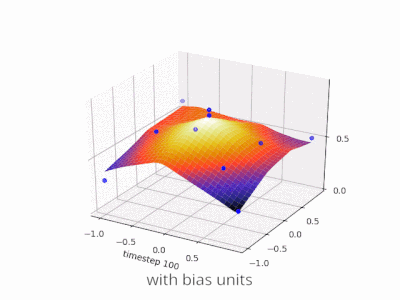
Эта тема действительно помогла мне разработать собственный проект. Вот еще несколько иллюстраций, показывающих результат простой двухслойной нейронной сети с прямой связью с блоками смещения и без нее в задаче регрессии с двумя переменными. Веса инициализируются случайным образом и используется стандартная активация ReLU. Как пришли к выводу ответы передо мной, без смещения ReLU-сеть не может отклоняться от нуля при (0,0).
Два разных вида параметров могут быть отрегулированы во время обучения ANN, весов и значений в функциях активации. Это нецелесообразно, и было бы проще, если бы был настроен только один из параметров. Чтобы справиться с этой проблемой, изобретен нейрон смещения. Смещающий нейрон лежит в одном слое, связан со всеми нейронами в следующем слое, но ни с одним на предыдущем слое, и он всегда излучает 1. Поскольку смещающий нейрон излучает 1, веса, связанные с нейроном смещения, добавляются непосредственно к объединенная сумма других весов (уравнение 2.1), как и значение t в функциях активации. 1
Причина, по которой это нецелесообразно, заключается в том, что вы одновременно корректируете вес и значение, поэтому любое изменение веса может нейтрализовать изменение значения, которое было полезно для предыдущего экземпляра данных... добавление нейрона смещения без изменения значения позволяет вам контролировать поведение слоя.
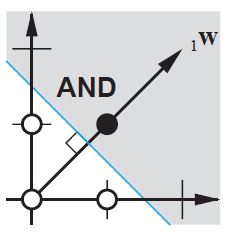
Кроме того, смещение позволяет использовать одну нейронную сеть для представления похожих случаев. Рассмотрим логическую функцию AND, представленную следующей нейронной сетью:
http://www.aihorizon.com/images/essays/perceptron.gif
- w0 соответствует b.
- w1 соответствует x1.
- w2 соответствует x2.
Один персептрон может использоваться для представления множества логических функций.
Например, если мы примем логические значения 1 (истина) и -1 (ложь), то одним из способов использования персептрона с двумя входами для реализации функции AND является установка весов w0 = -3 и w1 = w2 = 0,5. Этот персептрон можно сделать так, чтобы он представлял функцию ИЛИ, изменив порог на w0 = -.3. Фактически, И и ИЛИ могут рассматриваться как особые случаи функций m-of-n: то есть функций, в которых по крайней мере m из n входов в персептрон должно быть истинным. Функция OR соответствует m = 1, а функция AND - m = n. Любую функцию m-of-n легко представить с помощью персептрона, установив все входные веса на одно и то же значение (например, 0,5), а затем соответствующим образом установив порог w0.
Персептроны могут представлять все примитивные логические функции AND, OR, NAND ( 1 AND) и NOR ( 1 OR). Машинное обучение - Том Митчелл)
Порог - это смещение, а w0 - вес, связанный с нейроном смещения / порога.
Уклон не является NN термин, это общий термин алгебры, чтобы рассмотреть.
Y = M*X + C (уравнение прямой)
Сейчас если C(Bias) = 0 тогда линия всегда будет проходить через начало координат, т.е. (0,0)и зависит только от одного параметра, т.е. MЭто наклон, поэтому у нас меньше вещей для игры.
C, который является смещением, принимает любое число и обладает активностью для смещения графика, и, следовательно, способен представлять более сложные ситуации.
В логистической регрессии ожидаемое значение цели преобразуется функцией связи, чтобы ограничить ее значение единичным интервалом. Таким образом, предсказания модели можно рассматривать как вероятности первичного исхода, как показано ниже: сигмоидальная функция в Википедии
Это последний активационный слой в карте NN, который включает и выключает нейрон. Здесь также играет роль смещение, и оно гибко смещает кривую, чтобы помочь нам отобразить модель.
Слой в нейронной сети без смещения является не чем иным, как умножением входного вектора на матрицу. (Выходной вектор может быть пропущен через сигмовидную функцию для нормализации и для последующего использования в многослойной сети ANN, но это не важно.)
Это означает, что вы используете линейную функцию и, следовательно, вход всех нулей всегда будет отображаться на выход всех нулей. Это может быть разумным решением для некоторых систем, но в целом оно слишком ограничительно.
Используя смещение, вы фактически добавляете другое измерение к вашему входному пространству, которое всегда принимает значение, равное единице, поэтому вы избегаете входного вектора всех нулей. Вы не теряете общности из-за этого, потому что ваша обученная матрица веса не должна быть сюръективной, поэтому она все равно может отображать все возможные ранее значения.
2d ANN:
Для ANN, отображающего два измерения в одно измерение, как при воспроизведении функций AND или OR (или XOR), вы можете думать о нейронной сети как о следующем:
На плоскости 2d отметьте все позиции входных векторов. Итак, для логических значений вы бы хотели отметить (-1,-1), (1,1), (-1,1), (1,-1). Теперь ваша ANN рисует прямую линию на плоскости 2d, отделяя положительный выход от отрицательных выходных значений.
Без смещения эта прямая линия должна проходить через ноль, в то время как с помощью смещения вы можете положить ее куда угодно. Итак, вы увидите, что без смещения вы столкнулись с проблемой с функцией AND, поскольку вы не можете поместить и (1, -1), и (-1,1) в отрицательную сторону. (Они не могут быть на линии.) Проблема равна для функции ИЛИ. Однако с уклоном легко провести черту.
Обратите внимание, что функция XOR в этой ситуации не может быть решена даже с предвзятым отношением.
Когда вы используете ANN, вы редко знаете о внутренностях систем, которые вы хотите изучить. Некоторые вещи не могут быть изучены без предвзятости. Например, взгляните на следующие данные: (0, 1), (1, 1), (2, 1), в основном это функция, которая отображает любой x на 1.
Если у вас есть одноуровневая сеть (или линейное отображение), вы не можете найти решение. Однако, если у вас есть предвзятость, это тривиально!
В идеальном случае смещение может также отобразить все точки на среднее значение целевых точек и позволить скрытым нейронам моделировать различия от этой точки.
Модификация нейронов ВЕСА сама по себе служит только для манипулирования формой / кривизной вашей передаточной функции, а не ее точкой равновесия / пересечения нуля.
Введение нейронов смещения позволяет смещать кривую передаточной функции по горизонтали (влево / вправо) вдоль входной оси, оставляя форму / кривизну без изменений. Это позволит сети генерировать произвольные выходные данные, отличные от значений по умолчанию, и, следовательно, вы можете настроить / сместить отображение ввода-вывода в соответствии с вашими конкретными потребностями.
Смотрите здесь для графического объяснения: http://www.heatonresearch.com/wiki/Bias
В нескольких экспериментах в моей магистерской диссертации (например, на странице 59) я обнаружил, что смещение может быть важным для первого (ых) слоя (ов), но особенно в полностью связанных слоях в конце оно, похоже, не играет большой роли.
Это может сильно зависеть от сетевой архитектуры / набора данных.
Просто добавить ко всему этому то, чего очень не хватает, а остальное, скорее всего, не знает.
Если вы работаете с изображениями, вы можете вообще не использовать смещение. Теоретически, таким образом ваша сеть будет более независимой от величины данных, например, будет ли изображение темным или ярким и ярким. И сеть научится выполнять свою работу, изучая относительность внутри ваших данных. Многие современные нейронные сети используют это.
Для других данных наличие смещения может быть критическим. Это зависит от типа данных, с которыми вы имеете дело. Если ваша информация не зависит от величины --- если ввод [1,0,0,1] должен привести к тому же результату, что и ввод [100,0,10], вам может быть лучше без смещения.
Смещение решает, на какой угол вы хотите, чтобы ваш вес вращался.
В 2-мерной диаграмме вес и смещение помогают нам найти границу принятия решений. Скажем, нам нужно построить функцию AND, пара input(p)-output(t) должна быть
{p=[0,0], t=0},{p=[1,0], t=0},{p=[0,1], t=0},{p=[1,1], t=1}
Теперь нам нужно найти границу решения, граница идеи должна быть:
Увидеть? W перпендикулярно нашей границе. Таким образом, мы говорим, что W решил направление границы.
Тем не менее, трудно найти правильный W в первый раз. В основном мы выбираем исходное значение W случайным образом. Таким образом, первая граница может быть такой: 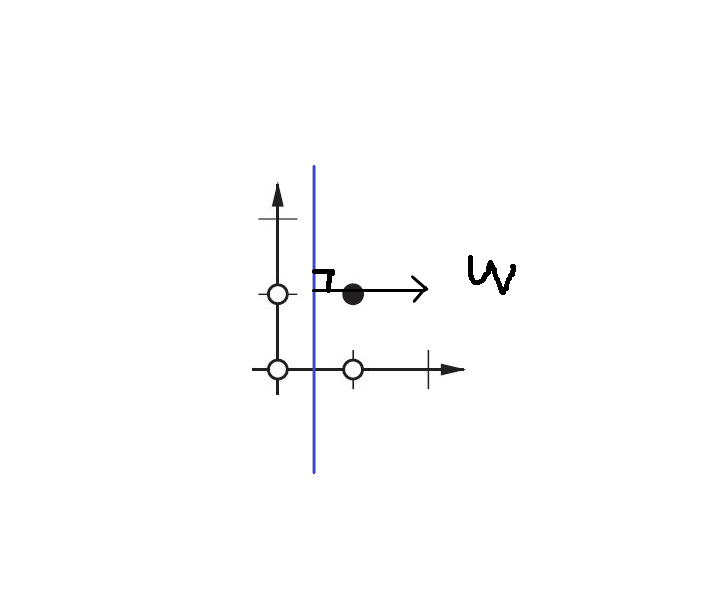
Теперь граница ближе к оси y.
Мы хотим повернуть границу, как?
Изменяя W.
Итак, мы используем функцию правила обучения: W'= W + P: 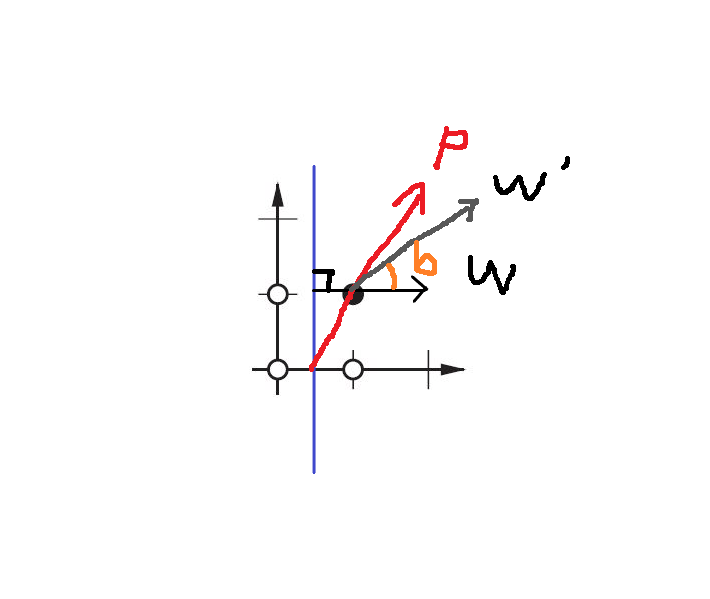
W'= W + P эквивалентно W'=W+bP, а b=1.
Поэтому, изменяя значение b(смещение), вы можете определить угол между W'и W. Это "правило обучения ANN".
Вы также можете прочитать " Проект нейронной сети" Мартина Т. Хагана / Говарда Б. Демута / Марка Х. Била, глава 4 "Правило обучения перцептрона"
В частности, ответ Нейта, ответ Зфи и ответ Пради великолепны.
Проще говоря, смещения позволяют изучать / хранить все больше и больше вариаций весов (примечание: иногда с некоторым порогом). В любом случае, больше вариаций означает, что смещения добавляют более полное представление входного пространства к изученным / сохраненным весам модели. (Где лучшие веса могут увеличить способность угадывания нейронной сети)
Например, в моделях обучения гипотеза / предположение желательно ограничено y=0 или y=1 при некотором входном сигнале, возможно, в некоторой задаче классификации... т.е. некотором y=0 для некоторого x=(1,1) и некоторых у = 1 для некоторого х =(0,1). (Условием для гипотезы / результата является пороговое значение, о котором я говорил выше. Обратите внимание, что в моих примерах входы X каждого элемента представляют собой x = двойной или 2-значный вектор вместо однозначных x входных данных Нейта некоторой коллекции X).
Если мы игнорируем смещение, многие входные данные могут в конечном итоге быть представлены множеством одинаковых весов (т. Е. Выученные веса в основном встречаются близко к началу координат (0,0). В этом случае модель будет ограничена меньшими количествами хороших весов, вместо гораздо большего количества хороших весов он мог бы лучше учиться с предвзятостью (где плохо изученные веса приводят к худшим догадкам или уменьшению способности угадывать нейронной сети)
Таким образом, оптимальным является то, что модель обучается как близко к началу координат, так и в максимально возможном количестве мест внутри границы порога / решения. При наличии предвзятости мы можем обеспечить степень свободы, близкую к источнику, но не ограниченную непосредственной областью происхождения.
Проще говоря, если у вас есть y=w1*x, где y - ваш вывод, а w1 - вес, представьте условие, где x=0, тогда y=w1*x равно 0. Если вы хотите обновить свой вес, у вас есть Чтобы вычислить, насколько изменилось значение delw = target-y, где target - это целевой результат, в этом случае "delw" не изменится, поскольку y вычисляется как 0. Так что, если вы можете добавить какое-то дополнительное значение, это поможет y=w1*x + w0 * 1, где смещение =1, и вес можно отрегулировать, чтобы получить правильное смещение. Рассмотрите пример ниже.
В терминах линии Наклон-перехват это особая форма линейных уравнений.
у = х + Ь
проверьте изображение
здесь b (0,2)
если вы хотите увеличить его до (0,3), как вы будете делать это, изменив значение b, которое будет вашим смещением
Расширяя объяснение @zfy... Уравнение для одного входа, одного нейрона, одного выхода должно выглядеть так:
y = a * x + b * 1 and out = f(y)
где x - это значение из входного узла, а 1 - это значение смещения; y может быть непосредственно вашим выводом или передаваться в функцию, часто сигмовидную функцию. Также обратите внимание, что смещение может быть любым постоянным, но чтобы упростить все, мы всегда выбираем 1 (и, вероятно, это так часто, что @zfy сделал это, не показывая и не объясняя это).
Ваша сеть пытается выучить коэффициенты a и b для адаптации к вашим данным. Итак, вы можете понять, почему добавление элемента b * 1 позволяет лучше соответствовать большему количеству данных: теперь вы можете изменить как наклон, так и перехват.
Если у вас есть более одного ввода, ваше уравнение будет выглядеть так:
y = a0 * x0 + a1 * x1 + ... + aN * 1
Обратите внимание, что уравнение по-прежнему описывает один нейрон, одну выходную сеть; если у вас больше нейронов, вы просто добавляете одно измерение в матрицу коэффициентов, чтобы мультиплексировать входы во все узлы и суммировать вклад каждого узла.
Что вы можете написать в векторизованном формате как
A = [a0, a1, .., aN] , X = [x0, x1, ..., 1]
Y = A . XT
т.е., помещая коэффициенты в один массив и (входы + смещение) в другой, вы получаете желаемое решение в виде точечного произведения двух векторов (вам нужно переставить X, чтобы фигура была правильной, я написал XT как 'X транспонированный')
Таким образом, в конце вы также можете увидеть свое смещение как еще один вход, чтобы представить часть вывода, которая на самом деле не зависит от вашего ввода.
В нейронных сетях:
- Каждый нейрон имеет уклон
- Вы можете просмотреть смещение как порог (обычно противоположные значения порога)
- Взвешенная сумма от входных слоев + смещение решает активацию нейрона
- Смещение увеличивает гибкость модели.
В отсутствие смещения, нейрон не может быть активирован, рассматривая только взвешенную сумму от входного слоя. Если нейрон не активирован, информация от этого нейрона не передается через остальную часть нейронной сети.
Значение предвзятости легко усваивается.
Следуйте этому видео для более подробной информации
Для всех книг по ML, которые я изучал, W всегда определяется как индекс связи между двумя нейронами, что означает, что чем выше связь между двумя нейронами, тем сильнее будут передаваться сигналы от запускающего нейрона к целевому нейрону или Y= w * X в результате, чтобы поддерживать биологический характер нейронов, нам нужно сохранять 1 >=W >= -1, но в реальной регрессии W в итоге будет |W| >=1, что противоречит принципу работы нейронов, поэтому я предлагаю W= cos(theta), а 1 >=| соз (тета)| и Y= a * X = W * X + b, в то время как a = b + W = b + cos(тета), b является целым числом
Помимо упомянутых ответов.. Я хотел бы добавить некоторые другие моменты.
Уклон действует как наш якорь. Для нас это способ создать какую-то базовую линию, в которой мы не опускаемся ниже этого уровня. В терминах графа представьте, что y=mx+b - это y-пересечение этой функции.
output = input умножает значение веса и добавляет значение смещения, а затем применяет функцию активации.
Термин смещение используется для настройки конечной выходной матрицы, как это делает y-перехват. Например, в классическом уравнении y = mx + c, если c = 0, линия всегда будет проходить через 0. Добавление члена смещения обеспечивает большую гибкость и лучшее обобщение для нашей модели нейронной сети.
Смещение помогает получить лучшее уравнение
Представьте себе ввод и вывод как функцию y = ax + b и вам нужно поместить правую линию между входом (x) и выходом (y), чтобы минимизировать глобальную ошибку между каждой точкой и линией, если вы сохраните уравнение, подобное этому y = ax, у вас будет только один параметр для адаптации, даже если вы найдете лучший a минимизируя глобальную ошибку, это будет далеко от желаемого значения
Можно сказать, что систематическая ошибка делает уравнение более гибким для адаптации к лучшим значениям.
В общем, в машинном обучении мы имеем эту базовую формулу Компенсация отклонения от отклонения. Поскольку в NN у нас есть проблема переоснащения (проблема обобщения модели, когда небольшие изменения в данных приводят к большим изменениям в результате модели), и из-за этого мы имеем большую дисперсию, вводя небольшой уклон мог бы помочь. Рассматривая формулу выше, смещение отклонения отклонения, где смещение возводится в квадрат, следовательно, введение небольшого смещения может привести к значительному снижению дисперсии. Итак, внесите предвзятость, когда у вас есть большая дисперсия и опасность перегрузки.
Помимо упомянутых ответов.. Я хотел бы добавить некоторые другие моменты.
Уклон действует как наш якорь. Для нас это способ создать какую-то базовую линию, в которой мы не опускаемся ниже этого уровня. В терминах графа представьте, что y=mx+b - это y-пересечение этой функции.
output = input умножает значение веса и добавляет значение смещения, а затем применяет функцию активации.