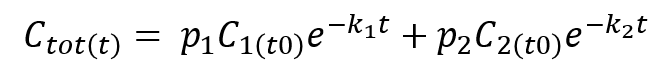"Отсутствует значение или бесконечность, полученная при оценке модели"

Question

Я пытаюсь решить двухкомпонентную модель распада в R, используя функцию nls, но сталкиваюсь с ошибками. Уравнение:

Где t - время, Ctot - это C1+C2, а p1 и p2 - известные пропорции Ctot.

мои данные (дд):

> head(dd,n=15)
      t    Ctot
1  0.00 6.62
2  0.33 6.45
3  0.50 6.38
4  0.67 6.44
5  0.83 6.38
6  1.00 6.39
7  1.17 6.35
8  1.33 6.33
9  1.50 6.33
10 1.67 6.28
11 1.83 6.17
12 2.00 6.11
13 2.17 6.07
14 2.33 5.89
15 2.50 5.86

Используя NLS, я попытался:

p1 <- 0.3
p2 <- 0.7   
z <- nls(Ctot~(p1*C1*(exp(-k1*t)))+(p2*C2*(exp(-k2*t))), data=dd, start=list(C1=6, C2=0.1, k1=0.01, k2=0.01))

Однако я получаю:

z <- nls(Ctot~(p1*C1*(exp(-k1*t)))+(p2*C2*(exp(-k2*t))), data=dd, start=list(C1=6, C2=0.1, k1=0.01, k2=0.01))
Error in numericDeriv(form[[3L]], names(ind), env) : 
  Missing value or an infinity produced when evaluating the model

Буду благодарен, если у кого есть предложения!

Answer 1

Данные кажутся довольно ограниченными и явно неполными, поскольку это только голова. Если мы составим некоторые данные для методов тестирования... и оставим в стороне запутанные p1 и p2:

 t=seq(0, 20, by=.3)
 Ctot = 3 * exp( -1 * t) + 4 * exp(-5*t)
 # following hte example on gnm::gnm's help page:

saved.fits <- list(); library(gnm)
for (i in 1:10) {
      saved.fits[[i]] <- suppressWarnings( gnm(Ctot ~ Exp(1 + t, inst = 1) +
                                                      Exp(1 + t, inst = 2),
                    verbose=FALSE))}
plot(Ctot~t)
lines(saved.fits[[3]]$fitted~t)
lines(saved.fits[[3]]$fitted~t,col="red")

Я не был знаком с пакетом gnm и поэтому прочитал первые несколько разделов, а затем обработанный пример подбора двухкомпонентных данных в его виньетке: https://cran.r-project.org/web/packages/gnm/vignettes/gnmOverview.pdf. Большинство совпадений будет таким, как ожидалось, но некоторые найдут локальный максимум по вероятности, который не является глобальным максимумом:

> saved.fits[[1]]$coefficients
                     (Intercept) Exp(. + t, inst = 1).(Intercept) 
                    1.479909e-12                     1.098612e+00 
          Exp(1 + ., inst = 1).t Exp(. + t, inst = 2).(Intercept) 
                   -1.000000e+00                     1.386294e+00 
          Exp(1 + ., inst = 2).t 
                   -5.000000e+00 
attr(,"eliminated")
[1] 0
> exp( saved.fits[[1]]$coefficients[4] )
Exp(. + t, inst = 2).(Intercept) 
                               4 
> exp( saved.fits[[1]]$coefficients[2] )
Exp(. + t, inst = 1).(Intercept) 
                               3 

Answer 2

С данными, показанными в вопросе, это, кажется, не работает хорошо, но если вы открыты для других параметрических моделей, тогда эта модель с 3 параметрами кажется разумной.

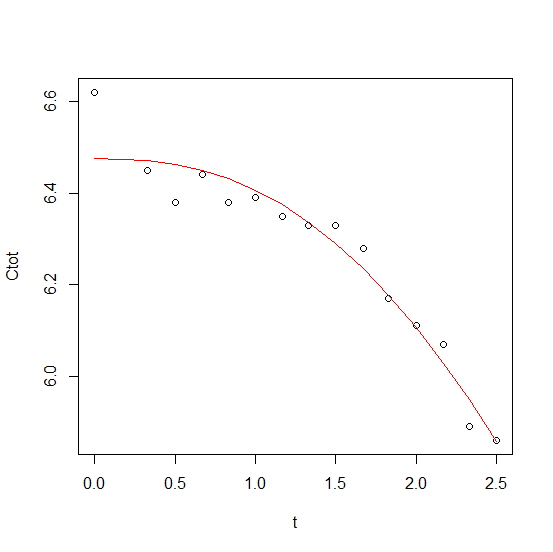
fm <- nls(Ctot ~ 1 / (a + b * t^c), dd, st = list(a = 1, b = 1, c = 1))
plot(dd)
lines(fitted(fm) ~ t, dd, col = "red")