Можно ли найти оптимальное решение для булевой формулы с помощью SMT-решателей?
У меня есть большая логическая формула для решения, из-за причины редактирования, я должен вставить изображение здесь:
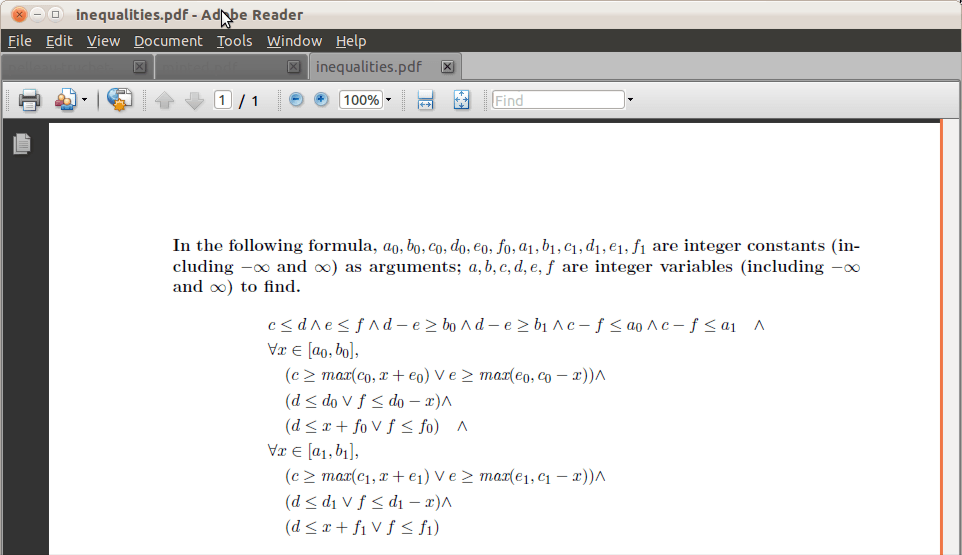
Также у меня уже есть функция area Чтобы измерить размерность 4 целых чисел: area(c,d,e,f)=|c−d|×|e−f|
Я хотел бы сделать больше, чем просто выяснить, удовлетворяет ли формула: я ищу оптимальный 6-кортеж (a,b,c,d,e,f) что делает большую формулу TRUE а также area(c,d,e,f) больше или равно размеру любого другого 6-ти кортежа, который также удовлетворяет формуле.
Другими словами, найти Max(area(c,d,e,f)) подчиняться большой формуле.
Мне интересно, если SMT решатель может помочь в решении этой проблемы. Я учу это Z3 опоры quantifiersи быть в состоянии сказать, является ли логическое выражение выполнимым или нет. Но вопрос в том, Z3 может помочь найти оптимальное решение для функции area,
У кого-нибудь есть идеи? Любые комментарии о SMT Solver, Z3 или других алгоритмах будут оценены...
4 ответа
Короче да.
Поскольку ваша формула состоит из квантификаторов, я не думаю, что Microsoft Solver Foundation является подходящим выбором. Как вы сказали, Z3 поддерживает кванторы, теорию целых чисел и используется для проверки выполнимости. Хотя Z3 напрямую не поддерживает оптимизацию, вы можете легко кодировать задачи оптимизации с помощью универсальных квантификаторов:
sat (a, b, c, d, e, f) => (для всех a1, b1, c1, d1, e1, f1. sat(a1, b1, c1, d1, e1, f1) && цель (a, b, c, d, e, f) >= цель (a1, b1, c1, d1, e1, f1))
где: sat ваше логическое выражение для проверки выполнимости и goal это area функция, ваша цель оптимизации.
Как видите, формулировка буквально переводится с вашего требования в вопросе. Назначение для (a, b, c, d, e, f) это оптимальное решение, которое вам нужно найти.
Кроме того, Z3 имеет дистрибутив Linux и предоставляет API-интерфейс OCaml, который полностью соответствует вашим предпочтениям.
Целевая функция использует нелинейную целочисленную арифметику и квантификаторы. Уже нелинейная целочисленная арифметика жесткая (неразрешимая) без квантификаторов, а добавление квантификаторов делает ее еще хуже. Если вы измените сортировку с Int на Real, то у нас будет очень ограниченное исключение квантификатора для нелинейных действительных значений ((set-option:ELIM_QUANTIFIERS true) (set-option:ELIM_NLARITH_QUANTIFIERS true)) Но это, похоже, не совсем подходит для проблема, которую вы, кажется, решаете. Попробуйте посмотреть, можно ли сформулировать ее как линейную или квадратичную задачу оптимизации. Есть много инструментов, которые настроены на квадратичную оптимизацию (и, возможно, они менее настроены на, скажем, логический поиск, которым является Z3). Попробуйте, например, Solver Foundation, который включает плагины для нескольких инструментов оптимизации.
Можно использовать Z3 для решения задач оптимизации, но типичным подходом является создание петли вне Z3. Сначала вы ставите задачу, которую вы хотите проверить, выполнимо, а затем вы ищете следующее удовлетворяющее назначение, которое улучшает текущее (которое вы извлекаете из удовлетворяющей модели). Для поиска следующего удовлетворительного назначения вы будете утверждать, что "цель", назначенная следующему искомому значению, улучшает "цель", назначенную текущему наилучшему значению.
Вот несколько слайдов http://research.microsoft.com/en-us/people/nbjorner/lecture1.pptx которые должны иметь отношение к делу. Они очень близки к решению этой проблемы. Последние несколько слайдов в этой колоде показывают, как использовать API Z3 для поиска по моделям. Конечно, вы также можете использовать текстовый API, если вы хотите написать синтаксический анализатор для выходного формата. Существует множество способов взаимодействия с Z3 для решения задач оптимизации, но все они требуют, чтобы вы запрограммировали поиск оптимизации поверх Z3. Это все еще может быть полезно, когда у вас есть логические комбинации ограничений по арифметике и другим областям, поддерживаемым Z3, но стандартные задачи оптимизации могут быть лучше решены с помощью специальных инструментов оптимизации.
Я считаю, что эта страница была бы чрезвычайно полезна. Пример хорошо объяснен, и он поможет прочитать весь пост.
Ваша проблема не совсем в удовлетворенности, а скорее в оптимизации или, более конкретно, в смешанном целочисленном программировании. Это не должно быть слишком сложно решить с помощью любого решателя, такого как (поскольку вы пометили свой вопрос Z3 и, похоже, вы используете Windows), Microsoft Solver Foundation, который также предлагает бесплатную версию.