Алгоритм выявления не неоднозначных кластеров?

Question

Алгоритмы кластеризации обычно принимают во внимание, что то, что человек может воспринимать как разумный кластер, является неоднозначным, и вычисленное решение должно хорошо обобщать и предсказывать.

Вот почему я не решаюсь использовать проверенные и проверенные алгоритмы для моей конкретной ситуации - это не значит, что я уверен, что они не будут работать или могут быть оптимальными. Я просто хотел бы проверить это.

Итак, давайте посмотрим на следующий пример.

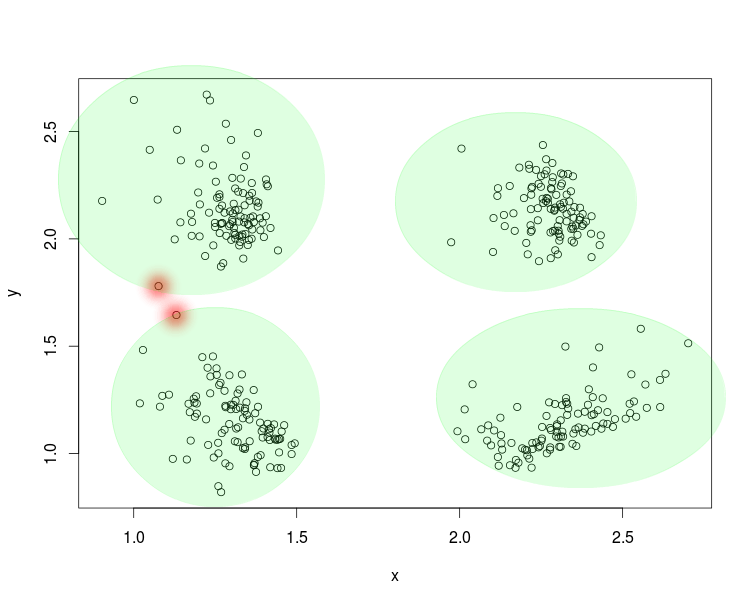
По сути, кластеры очевидны, за исключением исключений, поскольку они на самом деле линейно разделимы. Данные, на которые я ссылаюсь, являются двумерными. Кластеры следуют за неизвестным распределением с модой и являются независимыми.

Какой алгоритм работает (скорость, надежность, простота) хорошо для этого конкретного шаблона кластера?

---

rotate <- function(xy, deg, cen) {
  xy <- xy - cen
  return(c(
    xy[1] * cos(deg) - xy[2] * sin(deg), 
    xy[2] * cos(deg) + xy[1] * sin(deg)
  ) + cen)
}

G <- expand.grid(1:2,1:2)

S <- list()
N <- 100
for(i in 1:nrow(G)) {
  set <- data.frame(x = rgamma(N,3,2)*0.2 + G[i,1], y=rgamma(N,3,2)*.1 + G[i,2])
  S[[i]] <- t(apply(set,1,rotate,runif(1,0,pi),c(mean(set[,1]),mean(set[,2]))))
}

S <- do.call(rbind, S)

plot(S)

Answer 1

Вы можете попробовать альфа-формы. Это триангуляция Делоне с удаленными ребрами, превышающими альфа.

Answer 2

Стандартная кластеризация k-средних будет работать хорошо и быстро для изображения, которое вы дали. В целом, кластеризация k-средних будет хорошо работать для таких изображений, как ваша, за исключением тех случаев, когда некоторые из ваших кластеров представляют собой тощие отдельные эллипсоиды, а центр одного эллипсоида находится вблизи удаленных точек другого. Если это так, то вам, вероятно, лучше использовать одну из идей кластеризации, которая жадно группирует точки, которые являются наиболее близкими друг к другу, и затем иерархически продолжает объединять близлежащие группы точек, пока не будет достигнут порог расстояния между группами точек. (или до тех пор, пока вы не достигнете нужного количества кластеров, если заранее знаете количество кластеров).

Единственное, что касается кластеризации k-средних, это то, что если вы используете ее в готовом виде, вам нужно знать, сколько кластеров вы хотите иметь. Существуют способы выбора количества кластеров на основе данных, хотя, если вы не знаете, сколько кластеров выбрать, посмотрите онлайн, если вам интересно.

Answer 3

Большинство алгоритмов должны справляться с данными так же просто, как это.

Также взгляните на кластеризацию на основе плотности, такую ​​как среднее смещение, DBSCAN.

Но по сути, любой должен делать. Получите инструментарий с широким выбором алгоритмов, таких как ELKI, и попробуйте несколько.

Answer 4

Я согласен с предложениями кластеризации на основе плотности (например, среднее смещение). Я полагаю, вы имеете в виду, что каждая пара кластеров линейно разделима? Если вы хотите автоматически проверить, являются ли любые два кластера линейно разделимыми, похоже, что вы можете вычислить их выпуклые оболочки и проверить, пересекаются ли они: Определите, являются ли два класса линейно разделимыми (алгоритмически в 2D)

Таким образом, теоретически вы могли бы провести несколько испытаний среднего сдвига с различной пропускной способностью ядра, проверяя каждое на предмет линейной отделимости кластера с каждым другим кластером, а также отслеживая некоторый тип оценки кластера (см. Раздел "Оценка и оценка" здесь http://en.wikipedia.org/wiki/Cluster_analysis).

Хотя ваши данные могут выглядеть "очевидными", придумать общее решение, позволяющее всегда получать "очевидные" выходные данные, нетривиально, если вы не обладаете некоторыми знаниями предметной области, которыми можно воспользоваться. Например, если бы вы могли сделать так, чтобы пропускная способность ядра со средним сдвигом (соседство вокруг каждой точки, которую вы сильно весите) была функцией некоторого свойства домена, это могло бы быть проще.