Лениво связывая узел для 1-мерного динамического программирования
Несколько лет назад я прошел курс алгоритмов, где мы давали следующую задачу (или такую):
Есть здание
nэтажи с лифтом, который может подниматься только на 2 этажа одновременно и на 3 этажа одновременно. Используя динамическое программирование, напишите функцию, которая будет вычислять количество шагов, которое требуется лифту, чтобы добраться от полаiна полj,
Это очевидно легко при использовании подхода с учетом состояния: вы создаете массив длиной n элементов и заполняете его значениями. Вы могли бы даже использовать технически не сохраняющий состояние подход, который включает в себя накопление результата в виде его рекурсивной передачи. Мой вопрос заключается в том, как сделать это без учета состояния, используя ленивую оценку и завязывая узел.
Я думаю, что разработал правильную математическую формулу:
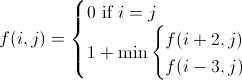
где i+2 а также i-3 находятся в пределах допустимых значений.
К сожалению, я не могу заставить его прекратить. Если я поставлю i+2 сначала выберите случай, а затем выберите ровный пол, чтобы оценить четные этажи ниже целевого уровня, но это все. Я подозреваю, что он стреляет прямо на самый высокий ровный этаж для всего остального, падает на 3 уровня, а затем повторяется, постоянно колебаясь между несколькими верхними этажами.
Так что это, вероятно, исследование бесконечного пространства (или конечного, но с петлями) в глубине в первую очередь. Я не могу думать о том, как исследовать пространство в широком смысле, не используя множество структур данных, которые эффективно имитируют подход с учетом состояния.
Хотя эта простая проблема разочаровывающе трудна, я подозреваю, что, увидев решение в 1-м измерении, я мог бы заставить его работать для 2-мерного варианта задачи.
РЕДАКТИРОВАТЬ: Многие ответы пытались решить проблему по-другому. Сама проблема мне не интересна, вопрос об используемом методе. Подход Хаосматтера к созданию minimal Функция, которая может сравнивать потенциально бесконечные числа, возможно, является шагом в правильном направлении. К сожалению, если я попытаюсь создать список, представляющий здание с 100 этажами, результат займет слишком много времени для вычисления, так как решения подзадач не используются повторно.
Я предпринял попытку использовать структуру данных с собственной ссылкой, но она не завершается, происходит какой-то бесконечный цикл. Я опубликую свой код, чтобы вы могли понять, для чего я иду. Я изменю принятый ответ, если кто-то действительно сможет решить проблему, используя динамическое программирование на самореференциальной структуре данных, используя лень, чтобы избежать вычислений более одного раза.
levels = go [0..10]
where
go [] = []
go (x:xs) = minimum
[ if i == 7
then 0
else 1 + levels !! i
| i <- filter (\n -> n >= 0 && n <= 10) [x+2,x-3] ]
: go xs
Вы можете увидеть, как 1 + levels !! i пытается ссылаться на ранее рассчитанный результат и как filter (\n -> n >= 0 && n <= 10) [x+2,x-3] пытается ограничить значения i к действительным. Как я уже сказал, на самом деле это не работает, а просто демонстрирует метод, с помощью которого я хочу, чтобы эта проблема была решена. Другие способы ее решения мне не интересны.
4 ответа
Поскольку вы пытаетесь решить это в двух измерениях и для других проблем, чем описанная, давайте рассмотрим некоторые более общие решения. Мы пытаемся решить проблему кратчайшего пути на ориентированных графах.
Наше представление графика в настоящее время что-то вроде a -> [a]где функция возвращает вершины, доступные из ввода. Любая реализация дополнительно потребует, чтобы мы могли сравнить, чтобы увидеть, совпадают ли две вершины, поэтому нам нужно Eq a,
Следующий график проблематичен и представляет почти все трудности в решении проблемы в целом:
problematic 1 = [2]
problematic 2 = [3]
problematic 3 = [2]
problematic 4 = []
При попытке достичь 4 из 1 существует цикл, включающий 2 и 3, который должен быть обнаружен, чтобы определить, что нет пути от 1 до 4.
Поиск в ширину
Алгоритм Уилла, если он применяется к общей задаче для конечных графов, имеет наихудшую производительность, неограниченную как во времени, так и в пространстве. Мы можем изменить его решение, чтобы атаковать общую проблему для графов, содержащих только конечные пути и конечные циклы, добавив обнаружение циклов. И его первоначальное решение, и эта модификация найдут конечные пути даже в бесконечных графах, но ни один из них не может надежно определить, что в бесконечном графе нет пути между двумя вершинами.
acyclicPaths :: (Eq a) => (a->[a]) -> a -> a -> [[a]]
acyclicPaths steps i j = map (tail . reverse) . filter ((== j).head) $ queue
where
queue = [[i]] ++ gen 1 queue
gen d _ | d <= 0 = []
gen d (visited:t) = let r = filter ((flip notElem) visited) . steps . head $ visited
in map (:visited) r ++ gen (d+length r-1) t
shortestPath :: (Eq a) => (a->[a]) -> a -> a -> Maybe [a]
shortestPath succs i j = listToMaybe (acyclicPaths succs i j)
Повторное использование step Функция ответа Уилла как определение вашей примерной задачи позволяет определить длину кратчайшего пути от 4 до 5 этажей 11-этажного здания. fmap length $ shortestPath (step 11) 4 5, Это возвращает Just 3,
Рассмотрим конечный граф с v вершинами и e ребрами. Граф с v вершинами и e ребрами может быть описан входом размера n ~ O(v+e). Граф наихудшего случая для этого алгоритма должен иметь одну недостижимую вершину, jи оставшиеся вершины и ребра, предназначенные для создания наибольшего числа ациклических путей, начиная с i, Это, вероятно, что-то вроде клики, содержащей все вершины, которые не являются i или же jс краями из i для каждой другой вершины, которая не j, Число вершин в клике с e ребрами равно O(e^(1/2)), поэтому этот граф имеет e ~ O(n), v ~ O(n^(1/2)). Этот граф будет иметь O((n^(1/2))!) Путей для исследования, прежде чем определить, что j недоступен
Объем памяти, требуемый этой функцией для этого случая, составляет O((n^(1/2))!), Поскольку для этого требуется только постоянное увеличение очереди для каждого пути.
Время, требуемое этой функцией для этого случая, составляет O((n^(1/2))! * N ^ (1/2)). Каждый раз, когда он расширяет путь, он должен проверить, что новый узел еще не находится в пути, что занимает O(v) ~ O(n^(1/2)) время. Это может быть улучшено до O(log (n^(1/2))), если бы мы имели Ord a и использовал Set a или аналогичная структура для хранения посещенных вершин.
Для не конечных графов эта функция не должна завершаться точно, только когда не существует конечного пути из i в j но существует бесконечный путь из i в j,
Динамическое программирование
Решение динамического программирования не обобщается таким же образом; давайте рассмотрим почему.
Для начала, мы адаптируем решение Chaosmasttter к тому же интерфейсу, что и наше решение поиска в ширину:
instance Show Natural where
show = show . toNum
infinity = Next infinity
shortestPath' :: (Eq a) => (a->[a]) -> a -> a -> Natural
shortestPath' steps i j = go i
where
go i | i == j = Zero
| otherwise = Next . foldr minimal infinity . map go . steps $ i
Это хорошо работает для проблемы с лифтом, shortestPath' (step 11) 4 5 является 3, К сожалению, для нашей проблемной проблемы, shortestPath' problematic 1 4 переполняет стек Если мы добавим немного больше кода для Natural номера:
fromInt :: Int -> Natural
fromInt x = (iterate Next Zero) !! x
instance Eq Natural where
Zero == Zero = True
(Next a) == (Next b) = a == b
_ == _ = False
instance Ord Natural where
compare Zero Zero = EQ
compare Zero _ = LT
compare _ Zero = GT
compare (Next a) (Next b) = compare a b
мы можем спросить, является ли кратчайший путь короче некоторой верхней границы. На мой взгляд, это действительно показывает то, что происходит с ленивой оценкой. problematic 1 4 < fromInt 100 является False а также problematic 1 4 > fromInt 100 является True,
Далее, чтобы исследовать динамическое программирование, нам нужно ввести некоторое динамическое программирование. Поскольку мы создадим таблицу решений всех подзадач, нам нужно будет знать возможные значения, которые могут принимать вершины. Это дает нам немного другой интерфейс:
shortestPath'' :: (Ix a) => (a->[a]) -> (a, a) -> a -> a -> Natural
shortestPath'' steps bounds i j = go i
where
go i = lookupTable ! i
lookupTable = buildTable bounds go2
go2 i | i == j = Zero
| otherwise = Next . foldr minimal infinity . map go . steps $ i
-- A utility function that makes memoizing things easier
buildTable :: (Ix i) => (i, i) -> (i -> e) -> Array i e
buildTable bounds f = array bounds . map (\x -> (x, f x)) $ range bounds
Мы можем использовать это как shortestPath'' (step 11) (1,11) 4 5 или же shortestPath'' problematic (1,4) 1 4 < fromInt 100, Это все еще не может обнаружить циклы...
Динамическое программирование и обнаружение цикла
Определение цикла проблематично для динамического программирования, потому что подзадачи не одинаковы, когда к ним подходят с разных путей. Рассмотрим вариант нашего problematic проблема.
problematic' 1 = [2, 3]
problematic' 2 = [3]
problematic' 3 = [2]
problematic' 4 = []
Если мы пытаемся получить от 1 в 4У нас есть два варианта:
- идти к
2и взять кратчайший путь из2в4 - идти к
3и взять кратчайший путь из3в4
Если мы решим исследовать 2, мы столкнемся со следующим вариантом:
- идти к
3и взять кратчайший путь из3в4
Мы хотим объединить два исследования кратчайшего пути из 3 в 4 в ту же запись в таблице. Если мы хотим избежать циклов, это действительно что-то более тонкое. Проблемы, с которыми мы столкнулись, были действительно:
- идти к
2и взять кратчайший путь из2в4это не посещает1 - идти к
3и взять кратчайший путь из3в4это не посещает1
После выбора 2
- идти к
3и взять кратчайший путь из3в4это не посещает1или же2
Эти два вопроса о том, как получить от 3 в 4 есть два слегка разных ответа. Это две разные подзадачи, которые не могут поместиться в одном месте таблицы. Ответ на первый вопрос в конечном итоге требует определения того, что вы не можете 4 от 2, Ответ на второй вопрос прост.
Мы могли бы сделать несколько таблиц для каждого возможного набора ранее посещенных вершин, но это не очень эффективно. Я почти убедил себя, что мы не можем сделать достижимость как проблему динамического программирования, используя только лень.
Поиск в ширину
Работая над решением динамического программирования с возможностью достижения или обнаружения цикла, я понял, что, как только мы увидим узел в опциях, дальнейшее посещение этого узла не может быть оптимальным, независимо от того, следуем ли мы этому узлу или нет. Если мы пересмотрим problematic':
Если мы пытаемся получить от 1 в 4У нас есть два варианта:
- идти к
2и взять кратчайший путь из2в4без посещения1,2, или же3 - идти к
3и взять кратчайший путь из3в4без посещения1,2, или же3
Это дает нам алгоритм, чтобы довольно легко найти длину кратчайшего пути:
-- Vertices first reachable in each generation
generations :: (Ord a) => (a->[a]) -> a -> [Set.Set a]
generations steps i = takeWhile (not . Set.null) $ Set.singleton i: go (Set.singleton i) (Set.singleton i)
where go seen previouslyNovel = let reachable = Set.fromList (Set.toList previouslyNovel >>= steps)
novel = reachable `Set.difference` seen
nowSeen = reachable `Set.union` seen
in novel:go nowSeen novel
lengthShortestPath :: (Ord a) => (a->[a]) -> a -> a -> Maybe Int
lengthShortestPath steps i j = findIndex (Set.member j) $ generations steps i
Как и ожидалось, lengthShortestPath (step 11) 4 5 является Just 3 а также lengthShortestPath problematic 1 4 является Nothing,
В худшем случае generations требуется пространство O(v*log v) и время O(v*e*log v).
Проблема в том, что min необходимо полностью оценить оба звонка fтак что если один из них зацикливается бесконечно min никогда не вернется. Таким образом, вы должны создать новый тип, кодирующий, что число, возвращаемое f Ноль или Преемник Ноля.
data Natural = Next Natural
| Zero
toNum :: Num n => Natural -> n
toNum Zero = 0
toNum (Next n) = 1 + (toNum n)
minimal :: Natural -> Natural -> Natural
minimal Zero _ = Zero
minimal _ Zero = Zero
minimal (Next a) (Next b) = Next $ minimal a b
f i j | i == j = Zero
| otherwise = Next $ minimal (f l j) (f r j)
where l = i + 2
r = i - 3
Этот код на самом деле работает.
Стоя на полу i из n этажное здание, найдите минимальное количество шагов, необходимых для того, чтобы добраться до пола j, где
step n i = [i-3 | i-3 > 0] ++ [i+2 | i+2 <= n]
таким образом, у нас есть дерево. нам нужно искать его в ширину, пока мы не получим узел, содержащий значение j, его глубина - это количество шагов. мы строим очередь, несущую уровни глубины,
solution n i j = case dropWhile ((/= j).snd) queue
of [] -> Nothing
((k,_):_) -> Just k
where
queue = [(0,i)] ++ gen 1 queue
Функция gen d p принимает свой вклад p от d отсекается от своей производственной точки вдоль очереди вывода:
gen d _ | d <= 0 = []
gen d ((k,i1):t) = let r = step n i1
in map (k+1 ,) r ++ gen (d+length r-1) t
Использует TupleSections. Здесь нет завязывания узлов, только базовый курс, т. Е. (Оптимистичное) форвардное производство и экономная разведка. Работает нормально без завязывания узлов, потому что мы ищем только первое решение. Если бы мы искали несколько из них, то нам нужно было бы как-то устранить циклы.
- см. также: https://en.wikipedia.org/wiki/Corecursion
С обнаружением цикла:
solutionCD1 n i j = case dropWhile ((/= j).snd) queue
of [] -> Nothing
((k,_):_) -> Just k
where
step n i visited = [i2 | let i2=i-3, not $ elem i2 visited, i2 > 0]
++ [i2 | let i2=i+2, not $ elem i2 visited, i2 <=n]
queue = [(0,i)] ++ gen 1 queue [i]
gen d _ _ | d <= 0 = []
gen d ((k,i1):t) visited = let r = step n i1 visited
in map (k+1 ,) r ++
gen (d+length r-1) t (r++visited)
например solution CD1 100 100 7 работает мгновенно, производя Just 31, visited list является в значительной степени копией экземпляра префикса самой очереди. Это может быть сохранено в виде карты, чтобы улучшить сложность времени (как это, sol 10000 10000 7 => Just 3331 на Ideone занимает 1,27 секунды).
Некоторые объяснения вроде бы в порядке.
Во-первых, нет ничего двумерного в вашей проблеме, потому что целевой этаж j фиксированный.
То, что вы, кажется, хотите, это запоминание, как показывает ваше последнее редактирование. Мемоизация полезна для рекурсивных решений; ваша функция действительно рекурсивна - она анализирует свой аргумент в под-кейсах, синтезирует свой результат из результатов вызова себя в под-кейсах (здесь i+2 а также i-3), которые ближе к базовому случаю (здесь, i==j).
Поскольку арифметика строгая, ваша формула расходится при наличии любого бесконечного пути в дереве шагов (идущего от пола к полу). Ответ от chaosmasttter, используя вместо этого ленивую арифметику, автоматически превращает его в алгоритм поиска в ширину, который расходится только в том случае, если в дереве нет конечных путей, точно так же, как мое первое решение выше (за исключением того факта, что он не проверяет Запредельные показатели). Но это все еще рекурсивно, так что действительно требуется запоминание.
Обычный способ сначала подойти к этому - ввести совместное использование, "просматривая список" (неэффективно из-за последовательного доступа; для эффективных решений по созданию памятей см. Раздел "Взлом"):
f n i j = g i
where
gs = map g [0..n] -- floors 1,...,n (0 is unused)
g i | i == j = Zero
| r > n = Next (gs !! l) -- assuming there's enough floors in the building
| l < 1 = Next (gs !! r)
| otherwise = Next $ minimal (gs !! l) (gs !! r)
where r = i + 2
l = i - 3
не испытано.
Мое решение является corecursive. Это не требует запоминания (просто нужно быть осторожным с дубликатами), потому что оно является генеративным, как динамическое программирование. Он уходит от своего стартового корпуса, то есть от стартового этажа. Внешний метод доступа выбирает соответствующий сгенерированный результат.
Это действительно завязывает узел - это определяет queue используя его - queue находится по обе стороны уравнения. Я считаю это более простым случаем завязывания узлов, потому что речь идет о замаскированном доступе к ранее сгенерированным значениям.
Связывание узлов 2-го рода, более сложного, обычно заключается в том, чтобы поместить некоторое еще неопределенное значение в некоторую структуру данных и вернуть его, чтобы оно было определено некоторой более поздней частью кода (например, указатель обратной ссылки в двойном связанный круговой список); это действительно не то, что делает мой 1 код. Что он делает, так это генерирует очередь, добавляет ее в конец и "удаляет" с ее фронта; в конце концов, это всего лишь методика списков различий в Prolog, открытый список с сохранением и обновлением его конечного указателя, построение нисходящего списка с хвостовой рекурсией по модулю cons - все это концептуально одно и то же. Впервые описан (хотя и не назван) в 1974 году, AFAIK.
1 полностью на основе кода из Википедии.
Другие ответили на ваш прямой вопрос о динамическом программировании. Тем не менее, для такого рода проблем я думаю, что жадный подход работает лучше всего. Его реализация очень проста.
f i j :: Int -> Int -> Int
f i j = snd $ until (\(i,_) -> i == j)
(\(i,x) -> (i + if i < j then 2 else (-3),x+1))
(i,0)