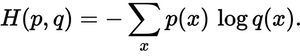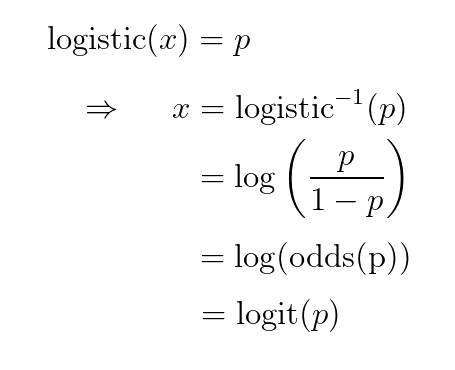Что такое logits, softmax и softmax_cross_entropy_with_logits?
Я просматривал здесь документы по тензорному API. В документации тензорного потока они использовали ключевое слово logits, Что это? Во многих методах в документации API это написано как
tf.nn.softmax(logits, name=None)
Если написано это те logits только Tensorsзачем сохранять другое имя, например logits?
Другое дело, что есть два метода, которые я не смог дифференцировать. Они были
tf.nn.softmax(logits, name=None)
tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None)
Каковы различия между ними? Документы мне не понятны. я знаю что tf.nn.softmax делает. Но не другой. Пример будет действительно полезным.
10 ответов
Logits просто означает, что функция работает с немасштабированным выходом более ранних слоев и что относительный масштаб для понимания единиц является линейным. В частности, это означает, что сумма входных данных может не равняться 1, что значения не являются вероятностями (у вас может быть входное значение 5).
tf.nn.softmax производит только результат применения функции softmax к входному тензору. Softmax "сдавливает" входы так, чтобы sum(input) = 1: это способ нормализации. Форма вывода softmax совпадает с формой ввода: она просто нормализует значения. Выводы softmax можно интерпретировать как вероятности.
a = tf.constant(np.array([[.1, .3, .5, .9]]))
print s.run(tf.nn.softmax(a))
[[ 0.16838508 0.205666 0.25120102 0.37474789]]
По сравнению, tf.nn.softmax_cross_entropy_with_logits вычисляет перекрестную энтропию результата после применения функции softmax (но делает все это вместе более математически тщательно). Это похоже на результат:
sm = tf.nn.softmax(x)
ce = cross_entropy(sm)
Перекрестная энтропия является суммарной метрикой: она суммирует элементы. Выход из tf.nn.softmax_cross_entropy_with_logits по форме [2,5] тензор имеет форму [2,1] (первое измерение рассматривается как партия).
Если вы хотите провести оптимизацию, чтобы минимизировать кросс-энтропию, и вы достигнете мягкого максимума после последнего слоя, вы должны использовать tf.nn.softmax_cross_entropy_with_logits вместо того, чтобы делать это самостоятельно, потому что он математически правильно охватывает численно нестабильные угловые случаи. В противном случае, вы в конечном итоге взломаете его, добавив маленькие эпсилоны здесь и там.
Отредактировано 2016-02-07: Если у вас есть метки одного класса, где объект может принадлежать только одному классу, вы можете теперь рассмотреть возможность использования tf.nn.sparse_softmax_cross_entropy_with_logits так что вам не нужно конвертировать ваши метки в плотный массив с одним горячим списком. Эта функция была добавлена после выпуска 0.6.0.
Укороченная версия:
Предположим, у вас есть два тензора, где y_hat содержит вычисленные оценки для каждого класса (например, из y = W*x +b) и y_true содержит горячие закодированные истинные метки.
y_hat = ... # Predicted label, e.g. y = tf.matmul(X, W) + b
y_true = ... # True label, one-hot encoded
Если вы интерпретируете баллы в y_hat как ненормализованные логарифмические вероятности, то они являются логитами.
Кроме того, общая потеря кросс-энтропии вычисляется следующим образом:
y_hat_softmax = tf.nn.softmax(y_hat)
total_loss = tf.reduce_mean(-tf.reduce_sum(y_true * tf.log(y_hat_softmax), [1]))
по существу эквивалентно полной кросс-энтропийной потере, вычисленной с помощью функции softmax_cross_entropy_with_logits():
total_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_hat, y_true))
Длинная версия:
В выходном слое вашей нейронной сети вы, вероятно, вычислите массив, который содержит оценки классов для каждого из ваших обучающих экземпляров, например, из вычислений y_hat = W*x + b, В качестве примера ниже я создал y_hat как массив 2 x 3, где строки соответствуют обучающим экземплярам, а столбцы соответствуют классам. Итак, здесь есть 2 тренировочных экземпляра и 3 класса.
import tensorflow as tf
import numpy as np
sess = tf.Session()
# Create example y_hat.
y_hat = tf.convert_to_tensor(np.array([[0.5, 1.5, 0.1],[2.2, 1.3, 1.7]]))
sess.run(y_hat)
# array([[ 0.5, 1.5, 0.1],
# [ 2.2, 1.3, 1.7]])
Обратите внимание, что значения не нормализованы (то есть строки не суммируют до 1). Чтобы их нормализовать, мы можем применить функцию softmax, которая интерпретирует входные данные как ненормализованные логарифмические вероятности (или логиты) и выводит нормализованные линейные вероятности.
y_hat_softmax = tf.nn.softmax(y_hat)
sess.run(y_hat_softmax)
# array([[ 0.227863 , 0.61939586, 0.15274114],
# [ 0.49674623, 0.20196195, 0.30129182]])
Важно полностью понимать, что говорит выход softmax. Ниже я показал таблицу, которая более четко представляет результат выше. Можно видеть, что, например, вероятность того, что тренировочный экземпляр 1 будет "Классом 2", составляет 0,619. Вероятности классов для каждого обучающего экземпляра нормированы, поэтому сумма каждой строки равна 1,0.
Pr(Class 1) Pr(Class 2) Pr(Class 3)
,--------------------------------------
Training instance 1 | 0.227863 | 0.61939586 | 0.15274114
Training instance 2 | 0.49674623 | 0.20196195 | 0.30129182
Итак, теперь у нас есть классовые вероятности для каждого обучающего экземпляра, где мы можем взять argmax() каждой строки, чтобы сгенерировать окончательную классификацию. Исходя из вышеизложенного, мы можем сгенерировать, что обучающий экземпляр 1 принадлежит "Классу 2", а обучающий экземпляр 2 принадлежит "Классу 1".
Верны ли эти классификации? Нам нужно сравнить с настоящими ярлыками из учебного набора. Вам понадобится горячая закодированная y_true массив, где снова строки - обучающие экземпляры, а столбцы - классы. Ниже я создал пример y_true один горячий массив, где истинная метка для обучающего экземпляра 1 - "Класс 2", а истинная метка для обучающего экземпляра 2 - "Класс 3".
y_true = tf.convert_to_tensor(np.array([[0.0, 1.0, 0.0],[0.0, 0.0, 1.0]]))
sess.run(y_true)
# array([[ 0., 1., 0.],
# [ 0., 0., 1.]])
Распределение вероятностей в y_hat_softmax близко к распределению вероятностей в y_true? Мы можем использовать кросс-энтропийную потерю для измерения ошибки.
Мы можем вычислить кросс-энтропийную потерю построчно и посмотреть результаты. Ниже мы видим, что тренировочный экземпляр 1 имеет потерю 0,479, в то время как тренировочный экземпляр 2 имеет большую потерю 1.200. Этот результат имеет смысл, потому что в нашем примере выше, y_hat_softmax показали, что наивысшая вероятность учебного экземпляра 1 была для "класса 2", что соответствует учебному экземпляру 1 в y_true; однако прогноз для обучающего экземпляра 2 показал наибольшую вероятность для "класса 1", который не соответствует истинному классу "класса 3".
loss_per_instance_1 = -tf.reduce_sum(y_true * tf.log(y_hat_softmax), reduction_indices=[1])
sess.run(loss_per_instance_1)
# array([ 0.4790107 , 1.19967598])
То, что мы действительно хотим, это полная потеря по всем тренировочным экземплярам. Таким образом, мы можем вычислить:
total_loss_1 = tf.reduce_mean(-tf.reduce_sum(y_true * tf.log(y_hat_softmax), reduction_indices=[1]))
sess.run(total_loss_1)
# 0.83934333897877944
Использование softmax_cross_entropy_with_logits()
Вместо этого мы можем вычислить общую кросс-энтропийную потерю, используя tf.nn.softmax_cross_entropy_with_logits() функция, как показано ниже.
loss_per_instance_2 = tf.nn.softmax_cross_entropy_with_logits(y_hat, y_true)
sess.run(loss_per_instance_2)
# array([ 0.4790107 , 1.19967598])
total_loss_2 = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_hat, y_true))
sess.run(total_loss_2)
# 0.83934333897877922
Обратите внимание, что total_loss_1 а также total_loss_2 производить по существу эквивалентные результаты с некоторыми небольшими различиями в самых последних цифрах. Тем не менее, вы могли бы также использовать второй подход: он занимает на одну строку кода меньше и накапливает меньше числовых ошибок, потому что softmax выполняется для вас внутри softmax_cross_entropy_with_logits(),
tf.nn.softmax вычисляет прямое распространение через слой softmax. Вы используете его во время оценки модели, когда вычисляете вероятности, которые выводит модель.
tf.nn.softmax_cross_entropy_with_logits вычисляет стоимость для слоя softmax. Он используется только во время обучения.
Логиты - это ненормализованные логарифмические вероятности, которые выводят модель (значения выводятся до того, как к ним применяется нормализация softmax).
В настройке, где мы хотим вывести значение, ограниченное от 0 до 1, но наша архитектура модели не ограничена в своих потенциальных выходных данных, мы можем добавить уровень нормализации в конце.
Обычным выбором является логистическая функция, в машинном обучении известная под более общим термином сигмовидная функция.
Если мы хотим интерпретировать выходные данные нашего нового последнего слоя как «вероятности», то по нашему выбору модели неограниченные входные данные для нашего сигмоида должны быть
inverse-sigmoid(вероятности). Оказывается, это эквивалентно логарифмическому коэффициенту нашей вероятности (поскольку он эквивалентен логарифму шансов ), иначе известному как <em>логит</em> :
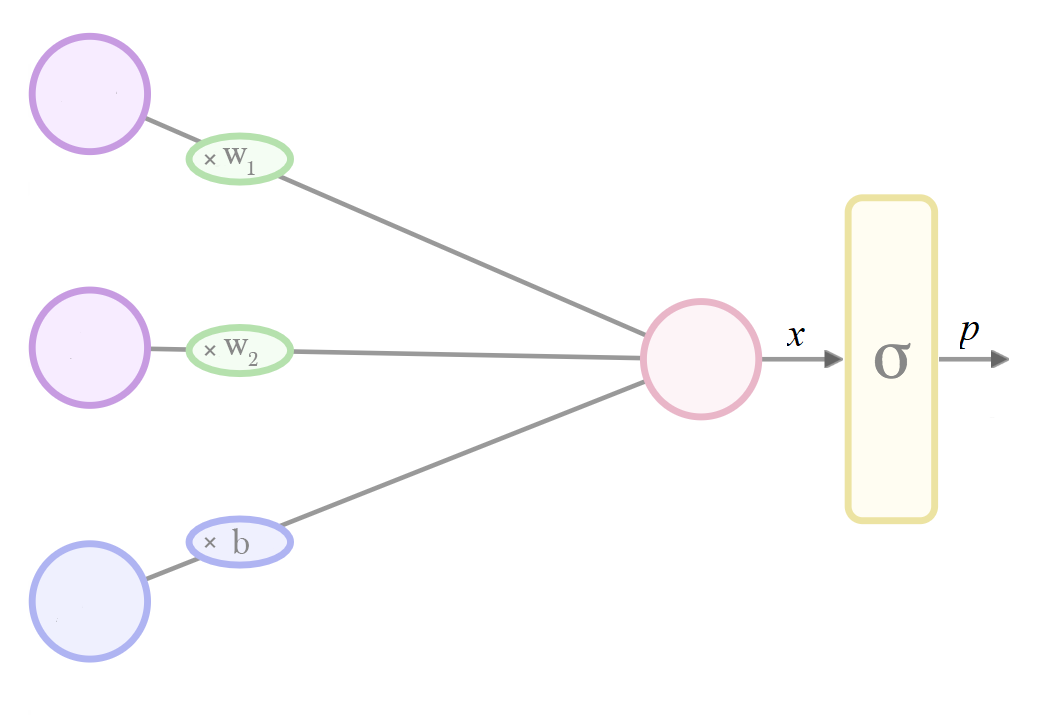
Поэтому аргументы этих функций называются
logit в Tensorflow - поскольку в предположении, что это последняя функция в модели, а выходные данные интерпретируются как вероятность, входные данные этого уровня интерпретируются как логит:
Что бы ни случилось softmax это логит, это то, что Дж. Хинтон постоянно повторяет в видеороликах coursera.
Приведенных выше ответов достаточно для описания задаваемого вопроса.
Кроме того, Tensorflow оптимизировал операцию применения функции активации, а затем расчета стоимости с использованием собственной активации, за которой следуют функции стоимости. Следовательно, это хорошая практика для использования: tf.nn.softmax_cross_entropy() над tf.nn.softmax(); tf.nn.cross_entropy()
Вы можете найти заметную разницу между ними в ресурсоемкой модели.
Ответ, совместимый с Tensorflow 2.0: объясненияdga а также stackruuser2010 очень подробно описаны Logits и связанные с ними функции.
Все эти функции при использовании в Tensorflow 1.x будет работать нормально, но если вы перенесете свой код из 1.x (1.14, 1.15, etc) к 2.x (2.0, 2.1, etc..), использование этих функций приведет к ошибке.
Следовательно, указание совместимых вызовов 2.0 для всех функций, которые мы обсуждали выше, если мы перейдем с 1.x to 2.x, на благо общества.
Функции в 1.x:
tf.nn.softmaxtf.nn.softmax_cross_entropy_with_logitstf.nn.sparse_softmax_cross_entropy_with_logits
Соответствующие функции при миграции с 1.x на 2.x:
tf.compat.v2.nn.softmaxtf.compat.v2.nn.softmax_cross_entropy_with_logitstf.compat.v2.nn.sparse_softmax_cross_entropy_with_logits
Дополнительные сведения о миграции с 1.x на 2.x см. В этом Руководстве по миграции.
Логиты — это ненормализованные выходные данные нейронной сети. Softmax — это функция нормализации, которая сжимает выходные данные нейронной сети так, чтобы все они были между 0 и 1 и в сумме давали 1. Softmax_cross_entropy_with_logits — это функция потерь, которая принимает выходные данные нейронной сети (после того, как они были сжаты softmax). и истинные метки для этих выходов и возвращает значение потерь.
Еще одна вещь, которую я определенно хотел бы выделить, поскольку logit - это просто необработанный вывод, обычно вывод последнего слоя. Это также может быть отрицательное значение. Если мы используем его для оценки "перекрестной энтропии", как указано ниже:
-tf.reduce_sum(y_true * tf.log(logits))
тогда это не сработает. Поскольку журнал -ve не определен. Таким образом, использование активации softmax решит эту проблему.
Это мое понимание, пожалуйста, поправьте меня, если я ошибаюсь.
Logit - это функция, которая отображает вероятности [0, 1] в [-inf, +inf]. Tensorflow "with logit": это означает, что вы применяете функцию softmax для логизации чисел для ее нормализации. Input_vector/logit не нормализован и может масштабироваться от [-inf, inf].
Эта нормализация используется для задач мультиклассовой классификации. А для задач классификации с несколькими метками используется нормализация сигмоидов, т.е. tf.nn.sigmoid_cross_entropy_with_logits