Использование return против не использования return в монаде списка

Question

Я начал свой Grand Haskell Crusade (GHC:)), и меня немного смущают монады и функции ввода-вывода. Может ли кто-нибудь просто объяснить, в чем разница между этими двумя функциями?

f1 = do x <- [1,2]
        [x, x+1] -- this is monad, right?

f2 = do x <- [1,2]
        return [x, x+1]

Результаты:

*Main> f1
[1,2,2,3]

*Main> f2
[[1,2],[2,3]]

Answer 1

Другие ответы здесь верны, но мне интересно, если они не совсем то, что вам нужно... Я постараюсь сделать это как можно проще, только два момента:

---

Пункт 1 return это не особенная вещь в языке Haskell. Это не ключевое слово, и это не синтаксический сахар для чего-то другого. Это просто функция, которая является частью Monad класс типов. Его подпись просто:

return :: a -> m a

где m это та монада, о которой мы говорим в то время. Он принимает "чистое" значение и превращает его в вашу монаду. (Кстати, есть еще одна функция с именем pure это в основном синоним return... мне больше нравится, потому что название более очевидно!) m это список монада, то return имеет этот тип:

return :: a -> [a]

Если это поможет, вы можете подумать о синониме типа type List a = [a] что может сделать это немного более очевидным, что List это то, что мы заменяем m, Во всяком случае, если вы собираетесь реализовать return сами, единственный разумный способ реализовать это, взяв какое-то значение (любого типа a) и поместим его в список отдельно:

return a = [a]

Так что могу сказать return 1 в списке монада, и я получу [1], Я могу также сказать return [1, 2, 3] и я получу [[1, 2, 3]],

---

Пункт 2 IO это монада, но не все монады IO , Многие учебники по Haskell, кажется, связывают две темы в основном по историческим причинам (кстати, те же самые запутанные исторические причины, которые привели к return будучи так плохо назван). Похоже, у вас может быть некоторая (понятная) путаница вокруг этого.

В вашем коде вы находитесь в списке монада, потому что вы написали do x <- [1, 2], Если вместо этого вы написали do x <- getLine например, вы бы в IO монада (потому что getLine возвращается IO String). В любом случае, вы находитесь в монаде списка, так что вы получите определение списка return описано выше. Вы также получите определение списка >>= Точнее (перевернутая версия) concatMap, определяется как:

concatMap :: (a -> [b]) -> [a] -> [b]
concatMap f xs = concat (map f xs)

Остальные опубликованные ответы в значительной степени отражены здесь:) Я знаю, что не ответил на ваш вопрос напрямую, но я надеюсь, что эти два пункта вместо этого касаются фундаментальных вещей, которые вы могли бы смущать.

Answer 2

Чтобы понять, почему вы получаете конкретные ответы, эти пояснения очень полезны. Позвольте мне дополнить их небольшим общим советом по разработке восприятия кода на Haskell.

Система типов Хаскелла не делает различий между двумя разделяемыми "моральными" целями:

• [x] тип значений, представляющих собой списки с элементами, взятыми из x
• [x] тип вычислений элементов x которые позволяют приоритетный выбор

Тот факт, что эти два понятия имеют одинаковое представление, не означает, что они играют одинаковые роли. В f1, [x, x+1] играет роль вычислений, поэтому возможности, которые он создает, объединяются с выбором, генерируемым целыми вычислениями: >>= из списка монада делает. В f2, Тем не менее [x, x+1] играет роль значения, так что все вычисления генерируют приоритетный выбор между двумя значениями (которые оказываются списочными значениями).

Хаскелл не использует типы, чтобы сделать это различие [и вы уже могли догадаться, что, как мне кажется, следует, но это уже другая история]. Вместо этого он использует синтаксис. Поэтому вам нужно тренировать свою голову, чтобы воспринимать значение и вычислительные роли при чтении кода. do нотация - это специальный синтаксис для построения вычислений. Что идет внутри do построен из следующего набора шаблонов:

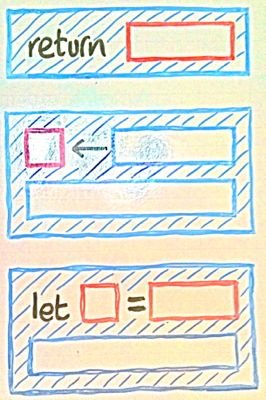
Три синие фигуры делают do-computations. Я отметил дыры в вычислениях синим цветом, а дыры в значениях - красным. Это не полный синтаксис, а всего лишь руководство к тому, как воспринимать фрагменты кода в уме.

Действительно, вы можете написать любое старое выражение в синих местах при условии, что оно имеет соответственно монадический тип, и сгенерированные таким образом вычисления будут объединены в общее вычисление с использованием >>= по мере необходимости. В вашем f1 Например, ваш список находится в синем месте и рассматривается как приоритетный выбор.

Точно так же вы можете писать выражения в красных местах, которые вполне могут иметь монадические типы (например, списки в этом случае), но они все равно будут рассматриваться как значения. Вот что происходит в f2: как бы внешние скобки результата синие, а внутренние красные.

Тренируйте свой мозг, чтобы разделить значение и вычисление при чтении кода, чтобы вы инстинктивно знали, какие части текста выполняют какую работу. Как только вы перепрограммируете свою голову, различие между f1 а также f2 будет казаться совершенно нормальным!

Answer 3

Это легко увидеть при переписывании кода с помощью bind и return:

[1,2] >>= (\x->        [x,x+1]) === concatMap (\x-> [  x,x+1  ]) [1,2]

[1,2] >>= (\x-> return [x,x+1]) === concatMap (\x-> [ [x,x+1] ]) [1,2]

Ваш первый код равносилен звонку join по результатам второго удаления одного монадического "слоя", введенного return :: a -> m a, сопоставляя "список" используемой монады с "списком" вашего значения. Если бы вы возвращали пару, скажем, было бы бессмысленно опускать return:

                                     -- WRONG: type mismatch
[1,2] >>= (\x->        (x,x+1)) === concatMap (\x-> (  x,x+1  )) [1,2]
                                     -- OK:
[1,2] >>= (\x-> return (x,x+1)) === concatMap (\x-> [ (x,x+1) ]) [1,2]

Или мы можем использовать join/fmap Перепишите:

ma >>= famb === join (fmap famb ma)   -- famb :: a -> m b, m ~ []

join (fmap (\x->        [x,x+1]) [1,2]) = concat [ [  x,x+1  ] | x<-[1,2]]
join (fmap (\x->        (x,x+1)) [1,2]) = concat [ (  x,x+1  ) | x<-[1,2]]  -- WRONG
join (fmap (\x-> return [x,x+1]) [1,2]) = concat [ [ [x,x+1] ] | x<-[1,2]]

                                                         =  [y | x<-[1,2], y<-[ x,x+1 ]]
                                            {- WRONG -}  =  [y | x<-[1,2], y<-( x,x+1 )]
                                                         =  [y | x<-[1,2], y<-[[x,x+1]]]

Answer 4

Тип списка ([]Монада, да.

Теперь запомни, что return делает. Это легко увидеть по типу подписи: return :: Monad m => a -> m a, Давайте заменим тип списка в: return :: a -> [a], Таким образом, эта функция принимает некоторое значение и возвращает только список этого значения. Это эквивалентно \ x -> [x],

Итак, в первом примере кода у вас есть один список в самом конце: [x, x+1], Во втором примере у вас есть вложенный список: один список приходит из [x, x + 1] и другой список исходит от return, Линия return [x, x + 1] может быть переписан [[x, x + 1]] в этом случае.

В конце, результат - список всех возможных результатов. То есть мы объединяем результат x как 1 и результат x как 2 (благодаря x <- [1,2] линия). Итак, в первом случае мы объединяем два списка; во втором случае мы объединяем два списка списков, потому что дополнительный return обернул результат в дополнительный список.

Answer 5

Desugaring do синтаксис к эквиваленту

f1 = [1,2] >>= \x -> [x, x+1]
f2 = [1,2] >>= \x -> return [x, x+1]

Сейчас, >>= исходит от Monad учебный класс,

class Monad m where
    (>>=) :: m a -> (a -> m b) -> m b
    return :: a -> m a

и LHS из >>= в обоих f1 а также f2 является [a] (где a по умолчанию Integer), поэтому мы действительно рассматриваем

instance Monad [] where
    (>>=) :: [a] -> (a -> [b]) -> [b]
    ...

Это подчиняется тем же законам монады, но отличается от монады,

instance Monad IO where ...

а также >>= для других монад, так что не применяйте вслепую то, что вы знаете об одном, к другому, хорошо?:)

instance Monad [] определяется таким образом в GHC

instance Monad [] where
    m >>= k = foldr ((++) . k) [] m
    return x = [x]
    ...

но это, вероятно, легче понять []"s >>= как

instance Monad [] where
    m >>= k = concatMap k m

Если вы возьмете это и примените к оригиналу, вы получите

f1 = concatMap (\x -> [x, x+1]) [1,2]
f2 = concatMap (\x -> [[x, x+1]]) [1,2]

и понятно, почему значения f1 а также f2 это то, что они есть.

Answer 6

Я понимаю, что делать

return [1,2], когда в списке монады то же самое, что и делать

func :: Maybe (Maybe Int)
func = return $ Just 1

вот почему вы получаете завернутые списки, так как [] просто синтаксический сахар, верно?

Когда на самом деле он хотел сделать

func :: Maybe Int
func = return 5

или же

func = Just 5

Я думаю, немного легче увидеть, что происходит с монадой "Может быть".

Итак, когда вы делаете

return [1,2]

Вы делаете так же, как

[ [1,2] ]