numpy: функция для одновременного max() и min()
numpy.amax() найдет максимальное значение в массиве, а numpy.amin() сделает то же самое для минимального значения. Если я хочу найти как max, так и min, мне нужно вызвать обе функции, что требует двойной передачи массива (очень большого), что кажется медленным.
Есть ли в numpy API функция, которая находит как max, так и min только с одним проходом данных?
13 ответов
Есть ли в numpy API функция, которая находит как max, так и min только с одним проходом данных?
Нет. На момент написания этой статьи такой функции не было. (И да, если бы была такая функция, ее производительность была бы значительно лучше, чем вызов numpy.amin() а также numpy.amax() последовательно на большом массиве.)
Я не думаю, что прохождение через массив дважды является проблемой. Рассмотрим следующий псевдокод:
minval = array[0]
maxval = array[0]
for i in array:
if i < minval:
minval = i
if i > maxval:
maxval = i
Хотя здесь есть только 1 цикл, есть еще 2 проверки. (Вместо того, чтобы иметь 2 петли с 1 проверкой каждый). На самом деле единственное, что вы сохраняете, это накладные расходы на 1 цикл. Если массивы действительно велики, как вы говорите, эти издержки невелики по сравнению с реальной рабочей нагрузкой цикла. (Обратите внимание, что все это реализовано в C, поэтому циклы в любом случае более или менее свободны).
РЕДАКТИРОВАТЬ Извините за 4 из вас, кто проголосовал и верил в меня. Вы определенно можете оптимизировать это.
Вот некоторый код Fortran, который может быть скомпилирован в модуль Python с помощью f2py (может быть Cython гуру может прийти и сравнить это с оптимизированной версией C...):
subroutine minmax1(a,n,amin,amax)
implicit none
!f2py intent(hidden) :: n
!f2py intent(out) :: amin,amax
!f2py intent(in) :: a
integer n
real a(n),amin,amax
integer i
amin = a(1)
amax = a(1)
do i=2, n
if(a(i) > amax)then
amax = a(i)
elseif(a(i) < amin) then
amin = a(i)
endif
enddo
end subroutine minmax1
subroutine minmax2(a,n,amin,amax)
implicit none
!f2py intent(hidden) :: n
!f2py intent(out) :: amin,amax
!f2py intent(in) :: a
integer n
real a(n),amin,amax
amin = minval(a)
amax = maxval(a)
end subroutine minmax2
Скомпилируйте это через:
f2py -m untitled -c fortran_code.f90
И теперь мы находимся в месте, где мы можем проверить это:
import timeit
size = 100000
repeat = 10000
print timeit.timeit(
'np.min(a); np.max(a)',
setup='import numpy as np; a = np.arange(%d, dtype=np.float32)' % size,
number=repeat), " # numpy min/max"
print timeit.timeit(
'untitled.minmax1(a)',
setup='import numpy as np; import untitled; a = np.arange(%d, dtype=np.float32)' % size,
number=repeat), '# minmax1'
print timeit.timeit(
'untitled.minmax2(a)',
setup='import numpy as np; import untitled; a = np.arange(%d, dtype=np.float32)' % size,
number=repeat), '# minmax2'
Результаты немного ошеломляющие для меня:
8.61869883537 # numpy min/max
1.60417699814 # minmax1
2.30169081688 # minmax2
Я должен сказать, я не полностью понимаю это. Сравнивая просто np.min против minmax1 а также minmax2 битва все еще проиграна, так что это не просто проблема с памятью...
примечания - Увеличение размера в 10**a и уменьшение повторения в 10**a (сохранение размера проблемы постоянным) действительно изменяет производительность, но не на первый взгляд согласованным образом, который показывает, что существует некоторая взаимосвязь между производительностью памяти и накладными расходами вызовов функций в python. Даже сравнивая простой min реализация в Фортране превосходит Numpy's примерно в 2 раза...
Вы можете использовать Numba, динамический компилятор Python с поддержкой NumPy, использующий LLVM. Полученная реализация довольно проста и понятна:
import numpy
import numba
@numba.jit
def minmax(x):
maximum = x[0]
minimum = x[0]
for i in x[1:]:
if i > maximum:
maximum = i
elif i < minimum:
minimum = i
return (minimum, maximum)
numpy.random.seed(1)
x = numpy.random.rand(1000000)
print(minmax(x) == (x.min(), x.max()))
Это также должно быть быстрее, чем Numpy's min() & max() реализация. И все это без необходимости писать одну строчку кода на C/Fortran.
Проведите собственные тесты производительности, так как они всегда зависят от вашей архитектуры, ваших данных, версий вашего пакета...
Существует функция для поиска (max-min), которая называется numpy.ptp, если это полезно для вас:
>>> import numpy
>>> x = numpy.array([1,2,3,4,5,6])
>>> x.ptp()
5
но я не думаю, что есть способ найти как мин, так и макс с одним обходом.
РЕДАКТИРОВАТЬ: PTP просто звонит мин и макс под капотом
Просто чтобы получить представление о числах, которых можно было ожидать, учитывая следующие подходы:
import numpy as np
def extrema_np(arr):
return np.max(arr), np.min(arr)
import numba as nb
@nb.jit(nopython=True)
def extrema_loop_nb(arr):
n = arr.size
max_val = min_val = arr[0]
for i in range(1, n):
item = arr[i]
if item > max_val:
max_val = item
elif item < min_val:
min_val = item
return max_val, min_val
import numba as nb
@nb.jit(nopython=True)
def extrema_while_nb(arr):
n = arr.size
odd = n % 2
if not odd:
n -= 1
max_val = min_val = arr[0]
i = 1
while i < n:
x = arr[i]
y = arr[i + 1]
if x > y:
x, y = y, x
min_val = min(x, min_val)
max_val = max(y, max_val)
i += 2
if not odd:
x = arr[n]
min_val = min(x, min_val)
max_val = max(x, max_val)
return max_val, min_val
%%cython -c-O3 -c-march=native -a
#cython: language_level=3, boundscheck=False, wraparound=False, initializedcheck=False, cdivision=True, infer_types=True
import numpy as np
cdef void _extrema_loop_cy(
long[:] arr,
size_t n,
long[:] result):
cdef size_t i
cdef long item, max_val, min_val
max_val = arr[0]
min_val = arr[0]
for i in range(1, n):
item = arr[i]
if item > max_val:
max_val = item
elif item < min_val:
min_val = item
result[0] = max_val
result[1] = min_val
def extrema_loop_cy(arr):
result = np.zeros(2, dtype=arr.dtype)
_extrema_loop_cy(arr, arr.size, result)
return result[0], result[1]
%%cython -c-O3 -c-march=native -a
#cython: language_level=3, boundscheck=False, wraparound=False, initializedcheck=False, cdivision=True, infer_types=True
import numpy as np
cdef void _extrema_while_cy(
long[:] arr,
size_t n,
long[:] result):
cdef size_t i, odd
cdef long x, y, max_val, min_val
max_val = arr[0]
min_val = arr[0]
odd = n % 2
if not odd:
n -= 1
max_val = min_val = arr[0]
i = 1
while i < n:
x = arr[i]
y = arr[i + 1]
if x > y:
x, y = y, x
min_val = min(x, min_val)
max_val = max(y, max_val)
i += 2
if not odd:
x = arr[n]
min_val = min(x, min_val)
max_val = max(x, max_val)
result[0] = max_val
result[1] = min_val
def extrema_while_cy(arr):
result = np.zeros(2, dtype=arr.dtype)
_extrema_while_cy(arr, arr.size, result)
return result[0], result[1]
(в extrema_loop_*()подходы аналогичны предлагаемым здесь, аextrema_while_*()подходы основаны на коде отсюда)
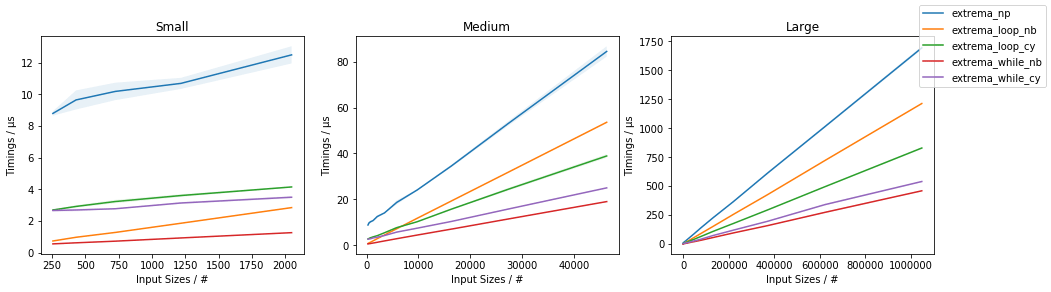
Следующие сроки:
указать, что extrema_while_*() самые быстрые, с extrema_while_nb()быть самым быстрым. В любом случае, такжеextrema_loop_nb() а также extrema_loop_cy() решения действительно превосходят подход NumPy-only (используя np.max() а также np.min() по отдельности).
Наконец, обратите внимание, что ни один из них не является таким гибким, как np.min()/np.max() (с точки зрения поддержки n-dim, axis параметр и т. д.).
(полный код доступен здесь)
Никто не упомянул numpy.percentile, поэтому я думал, что буду. Если вы попросите [0, 100] процентили, он даст вам массив из двух элементов: минимальный (0-й процентиль) и максимальный (100-й процентиль).
Тем не менее, он не удовлетворяет цели ОП: он не быстрее, чем min и max отдельно. Вероятно, это связано с некоторыми механизмами, которые допускают неэкстремальные процентили (более сложная проблема, которая должна занять больше времени).
In [1]: import numpy
In [2]: a = numpy.random.normal(0, 1, 1000000)
In [3]: %%timeit
...: lo, hi = numpy.amin(a), numpy.amax(a)
...:
100 loops, best of 3: 4.08 ms per loop
In [4]: %%timeit
...: lo, hi = numpy.percentile(a, [0, 100])
...:
100 loops, best of 3: 17.2 ms per loop
In [5]: numpy.__version__
Out[5]: '1.14.4'
Будущая версия Numpy может быть помещена в особый случай, чтобы пропустить расчет нормального процентиля, если только [0, 100] запрашиваются. Не добавляя ничего к интерфейсу, есть способ запросить у Numpy минимальное и максимальное значения за один вызов (вопреки тому, что было сказано в принятом ответе), но стандартная реализация библиотеки не использует этот случай, чтобы сделать это стоит.
В общем, вы можете уменьшить количество сравнений для алгоритма minmax, обрабатывая два элемента одновременно и сравнивая только меньший с временным минимумом и больший с временным максимумом. В среднем нужно только 3/4 сравнений, чем наивный подход.
Это может быть реализовано в c или fortran (или любом другом языке низкого уровня) и должно быть почти непобедимым с точки зрения производительности. Я использую numba, чтобы проиллюстрировать принцип и получить очень быструю, независимую от dtype реализацию:
import numba as nb
import numpy as np
@nb.njit
def minmax(array):
# Ravel the array and return early if it's empty
array = array.ravel()
length = array.size
if not length:
return
# We want to process two elements at once so we need
# an even sized array, but we preprocess the first and
# start with the second element, so we want it "odd"
odd = length % 2
if not odd:
length -= 1
# Initialize min and max with the first item
minimum = maximum = array[0]
i = 1
while i < length:
# Get the next two items and swap them if necessary
x = array[i]
y = array[i+1]
if x > y:
x, y = y, x
# Compare the min with the smaller one and the max
# with the bigger one
minimum = min(x, minimum)
maximum = max(y, maximum)
i += 2
# If we had an even sized array we need to compare the
# one remaining item too.
if not odd:
x = array[length]
minimum = min(x, minimum)
maximum = max(x, maximum)
return minimum, maximum
Это определенно быстрее, чем наивный подход, который представил Пек:
arr = np.random.random(3000000)
assert minmax(arr) == minmax_peque(arr) # warmup and making sure they are identical
%timeit minmax(arr) # 100 loops, best of 3: 2.1 ms per loop
%timeit minmax_peque(arr) # 100 loops, best of 3: 2.75 ms per loop
Как и ожидалось, новая реализация minmax занимает всего около 3/4 времени, которое заняла наивная реализация (2.1 / 2.75 = 0.7636363636363637)
Это старая ветка, но, в любом случае, если кто-нибудь еще раз посмотрит на это
При одновременном поиске минимального и максимального значений можно сократить количество сравнений. Если вы сравниваете поплавки (что, я думаю, так и есть), это может сэкономить вам время, но не вычислительную сложность.
Вместо (код Python):
_max = ar[0]
_min= ar[0]
for ii in xrange(len(ar)):
if _max > ar[ii]: _max = ar[ii]
if _min < ar[ii]: _min = ar[ii]
Вы можете сначала сравнить два соседних значения в массиве, а затем сравнить только меньшее с текущим минимумом и большее с текущим максимумом:
## for an even-sized array
_max = ar[0]
_min = ar[0]
for ii in xrange(0, len(ar), 2)): ## iterate over every other value in the array
f1 = ar[ii]
f2 = ar[ii+1]
if (f1 < f2):
if f1 < _min: _min = f1
if f2 > _max: _max = f2
else:
if f2 < _min: _min = f2
if f1 > _max: _max = f1
Код здесь написан на Python, очевидно, для скорости вы бы использовали C, Fortran или Cython, но таким образом вы делаете 3 сравнения за одну итерацию, с len(ar)/2 итерациями, что дает 3/2 * len(ar) сравнения. В отличие от этого, выполняя сравнение "очевидным образом", вы делаете два сравнения за итерацию, что приводит к 2 * len (ar) сравнениям. Экономит 25% времени на сравнение.
Может быть, кто-то когда-нибудь найдет это полезным.
На первый взгляд, numpy.histogram кажется, чтобы сделать трюк:
count, (amin, amax) = numpy.histogram(a, bins=1)
... но если вы посмотрите на источник для этой функции, он просто вызывает a.min() а также a.max() независимо, и, следовательно, не удается избежать проблем производительности, рассмотренных в этом вопросе.:-(
Так же, scipy.ndimage.measurements.extrema выглядит как возможность, но это тоже просто вызывает a.min() а также a.max() независимо.
В любом случае, для меня это стоило усилий, поэтому я предлагаю здесь самое сложное и наименее элегантное решение для всех, кто может быть заинтересован. Мое решение - реализовать многопоточный алгоритм min-max за один проход на C++ и использовать его для создания модуля расширения Python. Это требует дополнительных затрат на изучение того, как использовать API-интерфейсы Python и NumPy C / C++, и здесь я покажу код и дам небольшие пояснения и ссылки для тех, кто хочет пойти по этому пути.
Многопоточный мин. / Макс.
Здесь нет ничего особо интересного. Массив разбит на куски размеромlength / workers. Мин / макс рассчитывается для каждого фрагмента вfuture, которые затем сканируются на предмет глобального минимума / максимума.
// mt_np.cc
//
// multi-threaded min/max algorithm
#include <algorithm>
#include <future>
#include <vector>
namespace mt_np {
/*
* Get {min,max} in interval [begin,end)
*/
template <typename T> std::pair<T, T> min_max(T *begin, T *end) {
T min{*begin};
T max{*begin};
while (++begin < end) {
if (*begin < min) {
min = *begin;
continue;
} else if (*begin > max) {
max = *begin;
}
}
return {min, max};
}
/*
* get {min,max} in interval [begin,end) using #workers for concurrency
*/
template <typename T>
std::pair<T, T> min_max_mt(T *begin, T *end, int workers) {
const long int chunk_size = std::max((end - begin) / workers, 1l);
std::vector<std::future<std::pair<T, T>>> min_maxes;
// fire up the workers
while (begin < end) {
T *next = std::min(end, begin + chunk_size);
min_maxes.push_back(std::async(min_max<T>, begin, next));
begin = next;
}
// retrieve the results
auto min_max_it = min_maxes.begin();
auto v{min_max_it->get()};
T min{v.first};
T max{v.second};
while (++min_max_it != min_maxes.end()) {
v = min_max_it->get();
min = std::min(min, v.first);
max = std::max(max, v.second);
}
return {min, max};
}
}; // namespace mt_np
Модуль расширения Python
Здесь все начинает становиться некрасивым... Один из способов использования кода C++ в Python - реализовать модуль расширения. Этот модуль можно собрать и установить с помощьюdistutils.coreстандартный модуль. Полное описание того, что это влечет за собой, содержится в документации Python: https://docs.python.org/3/extending/extending.html. ПРИМЕЧАНИЕ: безусловно, есть и другие способы получить аналогичные результаты, цитируя https://docs.python.org/3/extending/index.html:
В этом руководстве рассматриваются только основные инструменты для создания расширений, предоставляемые как часть этой версии CPython. Сторонние инструменты, такие как Cython, cffi, SWIG и Numba, предлагают как более простые, так и более сложные подходы к созданию расширений C и C++ для Python.
По сути, этот путь скорее академический, чем практический. С учетом вышесказанного, что я сделал дальше, довольно близко придерживаясь этого руководства, создал файл модуля. По сути, это шаблон для distutils, который знает, что делать с вашим кодом, и создает из него модуль Python. Прежде чем делать что-либо из этого, вероятно, будет разумным создать виртуальную среду Python, чтобы не загрязнять системные пакеты (см. https://docs.python.org/3/library/venv.html).
Вот файл модуля:
// mt_np_forpy.cc
//
// C++ module implementation for multi-threaded min/max for np
#define NPY_NO_DEPRECATED_API NPY_1_7_API_VERSION
#include <python3.6/numpy/arrayobject.h>
#include "mt_np.h"
#include <cstdint>
#include <iostream>
using namespace std;
/*
* check:
* shape
* stride
* data_type
* byteorder
* alignment
*/
static bool check_array(PyArrayObject *arr) {
if (PyArray_NDIM(arr) != 1) {
PyErr_SetString(PyExc_RuntimeError, "Wrong shape, require (1,n)");
return false;
}
if (PyArray_STRIDES(arr)[0] != 8) {
PyErr_SetString(PyExc_RuntimeError, "Expected stride of 8");
return false;
}
PyArray_Descr *descr = PyArray_DESCR(arr);
if (descr->type != NPY_LONGLTR && descr->type != NPY_DOUBLELTR) {
PyErr_SetString(PyExc_RuntimeError, "Wrong type, require l or d");
return false;
}
if (descr->byteorder != '=') {
PyErr_SetString(PyExc_RuntimeError, "Expected native byteorder");
return false;
}
if (descr->alignment != 8) {
cerr << "alignment: " << descr->alignment << endl;
PyErr_SetString(PyExc_RuntimeError, "Require proper alignement");
return false;
}
return true;
}
template <typename T>
static PyObject *mt_np_minmax_dispatch(PyArrayObject *arr) {
npy_intp size = PyArray_SHAPE(arr)[0];
T *begin = (T *)PyArray_DATA(arr);
auto minmax =
mt_np::min_max_mt(begin, begin + size, thread::hardware_concurrency());
return Py_BuildValue("(L,L)", minmax.first, minmax.second);
}
static PyObject *mt_np_minmax(PyObject *self, PyObject *args) {
PyArrayObject *arr;
if (!PyArg_ParseTuple(args, "O", &arr))
return NULL;
if (!check_array(arr))
return NULL;
switch (PyArray_DESCR(arr)->type) {
case NPY_LONGLTR: {
return mt_np_minmax_dispatch<int64_t>(arr);
} break;
case NPY_DOUBLELTR: {
return mt_np_minmax_dispatch<double>(arr);
} break;
default: {
PyErr_SetString(PyExc_RuntimeError, "Unknown error");
return NULL;
}
}
}
static PyObject *get_concurrency(PyObject *self, PyObject *args) {
return Py_BuildValue("I", thread::hardware_concurrency());
}
static PyMethodDef mt_np_Methods[] = {
{"mt_np_minmax", mt_np_minmax, METH_VARARGS, "multi-threaded np min/max"},
{"get_concurrency", get_concurrency, METH_VARARGS,
"retrieve thread::hardware_concurrency()"},
{NULL, NULL, 0, NULL} /* sentinel */
};
static struct PyModuleDef mt_np_module = {PyModuleDef_HEAD_INIT, "mt_np", NULL,
-1, mt_np_Methods};
PyMODINIT_FUNC PyInit_mt_np() { return PyModule_Create(&mt_np_module); }
В этом файле широко используются Python, а также API NumPy, для получения дополнительной информации обратитесь: https://docs.python.org/3/c-api/arg.html и для NumPy.: https://docs.scipy.org/doc/numpy/reference/c-api.array.html.
Установка модуля
Следующее, что нужно сделать, это использовать distutils для установки модуля. Для этого требуется установочный файл:
# setup.py
from distutils.core import setup,Extension
module = Extension('mt_np', sources = ['mt_np_module.cc'])
setup (name = 'mt_np',
version = '1.0',
description = 'multi-threaded min/max for np arrays',
ext_modules = [module])
Чтобы окончательно установить модуль, выполните python3 setup.py install из вашей виртуальной среды.
Тестирование модуля
Наконец, мы можем проверить, действительно ли реализация C++ превосходит простое использование NumPy. Для этого вот простой тестовый скрипт:
# timing.py
# compare numpy min/max vs multi-threaded min/max
import numpy as np
import mt_np
import timeit
def normal_min_max(X):
return (np.min(X),np.max(X))
print(mt_np.get_concurrency())
for ssize in np.logspace(3,8,6):
size = int(ssize)
print('********************')
print('sample size:', size)
print('********************')
samples = np.random.normal(0,50,(2,size))
for sample in samples:
print('np:', timeit.timeit('normal_min_max(sample)',
globals=globals(),number=10))
print('mt:', timeit.timeit('mt_np.mt_np_minmax(sample)',
globals=globals(),number=10))
Вот результаты, которые я получил от всего этого:
8
********************
sample size: 1000
********************
np: 0.00012079699808964506
mt: 0.002468645994667895
np: 0.00011947099847020581
mt: 0.0020772050047526136
********************
sample size: 10000
********************
np: 0.00024697799381101504
mt: 0.002037393998762127
np: 0.0002713389985729009
mt: 0.0020942929986631498
********************
sample size: 100000
********************
np: 0.0007130410012905486
mt: 0.0019842900001094677
np: 0.0007540129954577424
mt: 0.0029724110063398257
********************
sample size: 1000000
********************
np: 0.0094779249993735
mt: 0.007134920000680722
np: 0.009129883001151029
mt: 0.012836456997320056
********************
sample size: 10000000
********************
np: 0.09471094200125663
mt: 0.0453535050037317
np: 0.09436299200024223
mt: 0.04188535599678289
********************
sample size: 100000000
********************
np: 0.9537652180006262
mt: 0.3957935369980987
np: 0.9624398809974082
mt: 0.4019058070043684
Это гораздо менее обнадеживающе, чем результаты, показанные ранее в потоке, которые указывают примерно на 3,5-кратное ускорение и не включают многопоточность. Достигнутые мной результаты в некоторой степени разумны, я ожидал, что накладные расходы на потоки будут преобладать во время, пока массивы не станут очень большими, и в этот момент повышение производительности начнет приближаться.std::thread::hardware_concurrency x увеличить.
Вывод
Казалось бы, есть место для оптимизации некоторого кода NumPy для конкретных приложений, в частности, в отношении многопоточности. Мне не ясно, стоит ли это усилий, но это определенно похоже на хорошее упражнение (или что-то в этом роде). Я думаю, что, возможно, изучение некоторых из этих "сторонних инструментов", таких как Cython, может быть более эффективным использованием времени, но кто знает.
Вдохновленный предыдущим ответом, я написал реализацию numba, возвращающую minmax для оси =0 из двумерного массива. Это примерно в 5 раз быстрее, чем вызов numpy min/max. Может кому пригодится.
from numba import jit
@jit
def minmax(x):
"""Return minimum and maximum from 2D array for axis=0."""
m, n = len(x), len(x[0])
mi, ma = np.empty(n), np.empty(n)
mi[:] = ma[:] = x[0]
for i in range(1, m):
for j in range(n):
if x[i, j]>ma[j]: ma[j] = x[i, j]
elif x[i, j]<mi[j]: mi[j] = x[i, j]
return mi, ma
x = np.random.normal(size=(256, 11))
mi, ma = minmax(x)
np.all(mi == x.min(axis=0)), np.all(ma == x.max(axis=0))
# (True, True)
%timeit x.min(axis=0), x.max(axis=0)
# 15.9 µs ± 9.4 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
%timeit minmax(x)
# 2.62 µs ± 31.3 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
Самый короткий способ, который я придумал, таков:
mn, mx = np.sort(ar)[[0, -1]]
Но поскольку он сортирует массив, он не самый эффективный.
Другой короткий способ:
mn, mx = np.percentile(ar, [0, 100])
Это должно быть более эффективным, но результат вычисляется и возвращается число с плавающей запятой.
Может быть, использоватьnumpy.unique? Вот так:
min_, max_ = numpy.unique(arr)[[0, -1]]
Просто добавил сюда для разнообразия :) Это так же медленно, как и сортировка.