Нелинейная оптимизация о точечных линиях
Я пытаюсь решить проблему нелинейной оптимизации с помощью библиотеки nlopt C++. Но результат, кажется, отличается от Matlab. Задача оптимизации заключается в следующем:
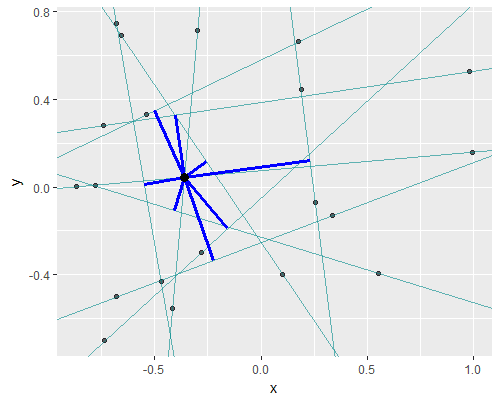
У меня есть линии, пересекающиеся с сервалами в трехмерной координате $l_i(x, y, z)$. И я хочу найти точку $(x_0, y_0, z_0)$, которая минимизирует расстояние от точки до всех этих линий. То есть... подробное описание проблемы на картинке.
#include <nlopt.hpp>
#include <math.h>
#include <iostream>
#include <vector>
struct Point {
double x;
double y;
double z;
Point() : x(0.0), y(0.0), z(0.0) {}
Point(double x_, double y_, double z_) :
x(x_), y(y_), z(z_) {}
};
Point operator-(const Point &p1, const Point &p2)
{
Point p;
p.x = p1.x - p2.x;
p.y = p1.y - p2.y;
p.z = p1.z - p2.z;
return p;
}
double operator*(const Point &p1, const Point &p2)
{
double ret = 0.0;
ret += (p1.x * p2.x + p1.y * p2.y + p1.z * p2.z);
return ret;
}
struct Line {
Point p1;
Point p2;
Line(const Point& p1_, const Point& p2_):
p1(p1_), p2(p2_) {}
};
int aux_calcu_func(const std::vector<double> &x,
const std::vector<Line> &lines,
double &obj, std::vector<double> &grad)
{
Point pCenter(x[0], x[1], x[2]);
// object function value
obj = 0.0;
for (size_t i = 0; i < lines.size(); ++i)
{
Line line = lines[i];
Point pA = line.p1;
Point pB = line.p2;
Point vAC = pCenter - pA;
Point vAB = pB - pA;
obj += (vAC * vAC - (vAC * vAB) * (vAC * vAB) / (vAB * vAB));
}
// gradient
if (!grad.empty())
{
for (size_t i = 0; i < lines.size(); ++i)
{
Line line = lines[i];
Point pA = line.p1;
Point pB = line.p2;
Point vAC = pCenter - pA;
Point vAB = pB - pA;
grad[0] += (2 * (vAC.x - (vAC * vAB * vAB.x / (vAB * vAB))));
grad[1] += (2 * (vAC.y - (vAC * vAB * vAB.y / (vAB * vAB))));
grad[2] += (2 * (vAC.z - (vAC * vAB * vAB.z / (vAB * vAB))));
}
}
return 0;
}
double my_func(const std::vector<double> &x, std::vector<double> &grad,
void *my_func_data)
{
Line *lines = reinterpret_cast<Line*>(my_func_data);
std::vector<Line> linesVec(lines, lines + 3);
double ret = 0.0;
if (0 != aux_calcu_func(x, linesVec, ret, grad))
{
throw "object function or gradient error!";
}
return ret;
}
int main(void)
{
// 3 lines
Line lines[3] = { { {0.6938, 2.0, 1.1678}, {0.6938, -2.0, 1.1811} },
{ {0.8723, 2.0, -0.8626},{0.8723, -2.0, 3.0110} },
{ {0.6080, 2.0, 0.4689}, {0.6080, -2.0, 0.5310} }
};
nlopt::opt opt(nlopt::LN_COBYLA, 3);
opt.set_min_objective(my_func, lines);
opt.set_xtol(1e-4);
std::vector<double> x(3);
x[0] = 0.0; x[1] = 0.0; x[2] = 0.0;
double minf = 0.0;
nlopt::result ret = opt.optimize(x, minf);
/* expected x = {1.0283, 0.7247, 0.3419},
* actually x = {0.7247, 0.2361, 0.8372}
*/
return 0;
}
1 ответ
Интересно, что эта проблема может быть эффективно решена как проблема SOCP (программирование конуса второго порядка). Не нужно ни производных, ни начальных точек, ни проверенных глобальных решений. В основном модель выглядит так:
С некоторыми случайными данными: