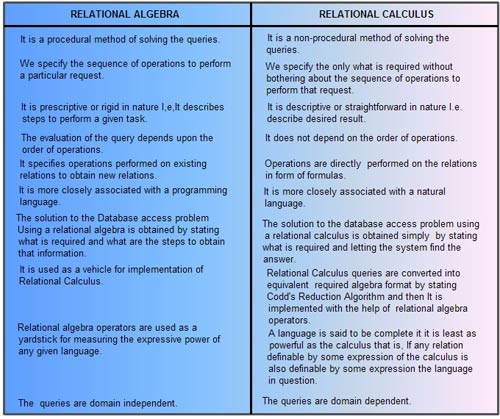
Разница между реляционной алгеброй и реляционным исчислением

Question

В чем точная разница между реляционной алгеброй и реляционным исчислением. По большей части это будет

Relational algebra is procedural and calculus is non procedural,

Итак, что это означает. Тем не менее, мы можем решить все проблемы, используя реляционную алгебру. Тогда почему мы будем использовать реляционное исчисление. Кроме определения, объяснение с примером очень ценится.

Answer 1

TL;DR: На самом деле это просто другой синтаксис для одной и той же вещи: значения отношения или свойства / условия, которым должны соответствовать кортежи значения отношения. Как и SQL. Как исчисление предикатов, язык математики, логики, науки (включая информатику) и инженерии (включая разработку программного обеспечения). А реляционная алгебра как процедурный против исчисления как декларативный - это миф.

---

Отношение содержит кортежи, которые превращают некоторый шаблон предиката - утверждения, параметризованный атрибутами - в истинное утверждение - утверждение.

/* tuples where employee PERSONNAME lives on STREET in CITY */
Employee
/* tuples where employee PERSONNAME works at COMPANY for $SALARY */
WorksFor

Выражение реляционной алгебры включает имена переменных / констант отношений, литералы отношений (имена и значения атрибутов) и операторы отношений. Это операторы JOIN, UNION, MINUS, PROJECT, RESTRICT и т. Д. Он обозначает значение отношения, которое вы получаете, вычисляя выражение, или любую перестановку выражения в соответствии с правилами, которые оставляют значение одинаковым.

/* RA query for tuples where
    FOR SOME STREET & CITY [employee PERSONNAME lives on STREET in CITY]
AND NOT FOR SOME COMPANY & SALARY
        [employee PERSONNAME works at COMPANY for $SALARY AND COMPANY = 'FBC']
*/
    PROJECT PERSONNAME (Employee)
MINUS PROJECT PERSONNAME (RESTRICT COMPANY = 'FBC' (WorksFor))

Исчисление домена имеет количественные имена, которые являются атрибутами. Мы используем сокращение для заявлений:

Employee(PERSONNAME, STREET, CITY)
    means (PERSONNAME, STREET, CITY) IN Employee
    means employee PERSONNAME lives on STREET in CITY
WorksFor(PERSONNAME, COMPANY, SALARY)
    means (PERSONNAME, COMPANY, SALARY) IN WorksFor
    means employee PERSONNAME works at COMPANY for $SALARY

/* DRC query for the same tuples as the RA query above */
rows like (PERSONNAME) where
    FOR SOME STREET & CITY [Employee(PERSONNAME, STREET, CITY)]
AND NOT EXISTS COMPANY & SALARY
        [WorksFor(PERSONNAME, COMPANY, SALARY) AND COMPANY = 'FBC']

Выражение реляционного исчисления включает в себя имена переменных / констант отношений, имена и значения атрибутов, операторы предикатов и количественные (логические переменные) имена. Операторы И, ИЛИ, НЕ, ДЛЯ НЕКОТОРЫХ / ВСЕХ и =. Он обозначает значение отношения, которое вы получаете, оценивая выражение или любую перестановку выражения в соответствии с правилами, которые оставляют значение тем же. Это обычно рассматривается как требования к стоимости, чтобы соответствовать.

Исчисление кортежей имеет имена логических переменных с кортежами. Мы ставим точку, чтобы получить значение, связанное с именем атрибута. (Как для поля записи языка программирования.) Мы используем сокращение для операторов:

Employee(T)
    means T IN Employee
    means employee T.PERSONNAME lives on T.STREET in T.CITY
    means (domain calculus) Employee(T.PERSONNAME, T.STREET, T.CITY)
Worksfor(T)
    means T IN Worksfor
    means employee T.PERSONNAME works at T.COMPANY for $T.SALARY
    means (domain calculus) Worksfor(T.PERSONNAME, T.COMPANY, T.SALARY)

/* TRC query for the same tuples as the RA query above */
rows like T with column PERSONNAME where
     FOR SOME E [Employee(E) AND E.PERSONNAME = T.PERSONNAME]
 AND NOT FOR SOME W [
        WorksFor(W)
    AND W.COMPANY = 'FBC'
    AND E.PERSONNAME = T.PERSONNAME
    ]

(Приводится несколько вариантов оригиналов алгебры и каждого исчисления. Например, некоторые идентифицируют аргументы по порядку, а другие - по имени. Иногда добавляются дополнительные возможности. Например, разрешение вызова функции в исчислении столь же выразительно, как и разрешение определенной константы отношения оператор плюс R переименовывает A в N в алгебре.)

Существует соответствие между операторами алгебры и операторами исчисления и между выражениями алгебры и выражениями исчисления, использующими их:

Если:
• R - содержит кортежи, где R(...)
• S - содержит кортежи, где S(...)
затем:
• R JOIN S содержит кортежи, где R(...) И S(...)
• R UNION S содержит кортежи, где R(...) ИЛИ S(...)
• R MINUS S содержит кортежи, где R(...) И НЕ S(...)
• R PROJECT столбцы для хранения содержит кортежи, где FOR SOME отбрасывать столбцы, R(...)
• Условие R RESTRICT содержит кортежи, в которых условие R(...) AND

Значение выражения алгебры - это кортежи, которые удовлетворяют соответствующему выражению исчисления.

Если мы хотим отобразить выражение из исчисления в выражение алгебры на основе оператор-оператор, нам нужен расширенный оператор, обобщающий UNION, и оператор, соответствующий NOT. Это не те операторы, которые мы хотели бы использовать в реализации. Но каждое исчисляемое выражение, использующее их, может быть механически преобразовано в нормальную форму, в которой используются только основные операторы алгебры.

Итак: реляционная алгебраически-процедурная против исчислительно-декларативная это миф. Каждый оператор алгебры имеет соответствующий оператор исчисления, каждый оператор исчисления имеет (возможно расширенный) соответствующий оператор алгебры, и каждое выражение одного имеет (в базовом и расширенном смысле) соответствующее выражение другого. Это две нотации для одних и тех же вещей. Выражение любого из них может быть принято как "процедурное", выполнив его как проанализированный или нормализованный, и как "декларативное", выполнив его в противном случае. Возможно, миф пытается уловить идею о том, что исчисление выражений не является оператор-оператором, как выражение, использующее основные операторы алгебры. Но выражение исчисления идентифицирует конкретное неочевидное выражение алгебры нормальной формы, используя базовые операторы, и является оператор-операторным, как выражение, использующее расширенный набор операторов алгебры.

(Миф, возможно, возник из-за истории слов. "Современная алгебра" имеет выражения с операторами, принимающими и дающими значения (чтобы их можно было вычислить). "Исчисление", то есть анализ (дифференцирование и интеграция), имеет выражения, описывающие значения как невозможно вычислить бесконечные суммы. Мы рассчитываем другими способами, в общем, только вычисляя приближения.)

(Также, по иронии судьбы, люди используют "исчисление предикатов", чтобы определять вещи "декларативно", независимо от того, как они могут быть вычислены или оценены иным образом, но стандартная семантика / значение такого выражения задается с помощью алгоритма, который обходит выражение дерево. Таким образом, оно имеет очевидную "процедурную" интерпретацию.)

Answer 2

перейдите по этой ссылке для деталей. http://ecomputernotes.com/database-system/rdbms/relational-algebra-and-relational-calculus

[

Answer 3

Эта презентация из класса NYU была очень полезна для меня. Я только изучаю это, поэтому я не могу быть слишком полезным, но я по крайней мере знаю, что реляционная алгебра имеет дело с более конкретными выражениями множеств, операциями соединения и комбинациями множеств, в то время как реляционное исчисление в основном придерживается отношений И-ИЛИ и либо экзистенциальный ("существует такой x, что [условие (x)])", либо универсальный ("для всех x, [условие (x)])". Я предполагаю, что реляционные алгебраические выражения похожи на язык ассемблера по функциональности и специфике, в то время как выражения реляционного исчисления ближе к языку программирования высокого уровня по внешнему виду и функциональности. Надеюсь, это поможет некоторым.

Answer 4

Разница между реляционной алгеброй и реляционным исчислением

1. Операции реляционной алгебры манипулируют некоторыми отношениями и предоставляют некоторое выражение в форме запросов, где в качестве реляционного исчисления формируются запросы на основе пар выражений.

2. RA имеет операторы, такие как соединение, объединение, пересечение, деление, различие, проекция, выбор и т. Д., Где в RC есть кортежи и доменно-ориентированные выражения.

3. RA - процедурный язык, где RC - не процедурная система запросов.

4. Выразительные силы RA и RC эквивалентны. Это означает, что любой запрос, который может быть выражен в RA, может быть выражен формулой в RC.

5. Любая формула KC переводится в алгебраический запрос.

6. Существует модификация, которая проще в запросах в RA, чем в RC.

7. RA сформировал математическую форму и не имеет специфического языка1. RC также имеет математическую форму, но имеет один язык запросов QUEL.

8. Реляционная алгебра легче манипулировать и понимать, чем RC.

9. Запросы RA более мощные, чем RC.

10. RC образуются WFFs, где RA не образует никакой формулы.

11. РА является процессуальным. Это означает, что мы должны написать некоторые условия по порядку.

12. RC не является процедурным. Здесь мы должны написать условия в любом порядке.

Пример:-

Пример библиотеки: -

Book is a relation it have a following attributes.

      1. Book Name
      2. Accession Number
      3. Year of publication

Проблема: -

 Find out the all book names published in the year 2000

Реляционная Алгебра: -

   -------------------------------------------------------
   |                       (σ            (book) )        |
   |       ¶                 (yr_pub=2000)               |
   |        (Book name)                                  |
    ------------------------------------------------------

Реляционное исчисление: -

    S = { t | ∃ u ∈  book (t[book name] = u[book name]) ∧ (u[yr_pub] = 2000 ) }

В этом реляционном исчислении мы можем записать условие в любом месте, как показано ниже.

    S = { t | ∃ u ∈  book  (u[yr_pub] = 2000 ) ∧ (t[book name] = u[book name])  }

Но в реляционной алгебре мы должны сначала найти, какие кортежи имеют год публикации 2000, а затем только мы должны извлечь столбец с именем книги.