Интуиция за минимизатором
Я очень новичок в количественном и научном программировании, и я столкнулся с функцией минимизатора scipy scipy.optimize.fmin, Может ли кто-нибудь объяснить мне основную интуицию этой функции для студентов, не являющихся инженерами?
Позвольте мне сказать, что я хочу минимизировать следующую функцию:
def f(x): x**2
1) Что минимизатор на самом деле минимизирует? Зависимая или независимая переменная?
2) Какая разница между scipy.optimize.fmin а также scipy.optimize.minimize?
2 ответа
Учитывая функцию, которая содержит некоторые неизвестные параметры (то есть фактически это семейство функций) и данные, минимизатор пытается найти параметры, которые минимизируют расстояние значений функции до данных. Это делается в разговорной речи путем итеративной корректировки параметров до тех пор, пока дальнейшие изменения не улучшат результат.
Это эквивалентно мячу, бегущему вниз по склону, упомянутому @pylang в комментарии. "Холм" - это расстояние до данных с учетом всех возможных значений параметров. Катящийся шарик - это минимизатор, который "перемещается" по этому ландшафту, проверяя параметры, пока не окажется в положении, когда каждое движение приведет к увеличению расстояния до данных или, по крайней мере, к заметному уменьшению.
Тем не менее, обратите внимание, что этим методом вы ищете локальный минимум значений функции для данных, учитывая набор параметров для функции. Для простой функции, как вы опубликовали, локальный минимум является единственным и, следовательно, глобальным, но для сложных функций, включающих много параметров, эта проблема быстро может стать довольно сложной.
Затем люди часто используют несколько прогонов минимизатора, чтобы увидеть, останавливается ли он на одной и той же позиции. Если это не так, люди говорят, что имитатор не сходится, что означает, что функция слишком сложна, чтобы легко найти один минимум. Есть много алгоритмов для противодействия этому, мне приходят в голову методы имитации отжига или методы Монте-Карло.
К вашей функции: функция f который упоминается в примере с помощью функции fmin, это функция расстояния. Он говорит вам, насколько далеко определенный набор параметров помещает вас относительно вашей цели. Теперь вы должны определить, что для вас значит расстояние. Обычно используется сумма квадратов невязок (также называемая евклидовой нормой):
sum((function values - data points)^2)
Скажи, у тебя есть функция
def f(x, a, b): return a*x**2 + b
Вы хотите найти значения для a а также b так что ваша функция максимально приближена к точкам данных, приведенным ниже, с соответствующими x а также y ценности:
datax = [ 0, 1, 2, 3, 4]
datay = [ 2, 3, 5, 9, 15]
Тогда, если вы используете евклидову норму, ваша функция расстояния (это функция f в fmin Помогите)
def dist(params):
a, b = params
return sum((f(x,a,b) - y)**2 for x,y in zip(datax, datay))
Вы должны быть в состоянии (извините, у меня нет scipy на моей текущей машине, проверю это сегодня вечером), чтобы свести к минимуму, чтобы получить соответствующие значения a а также b с помощью
import scipy.optimize
res = scipy.optimize.fmin(dist, x0 = (0,0))
Обратите внимание, что вам нужны начальные значения x0 для ваших параметров a а также b, Это значения, которые вы выбираете случайным образом, если вы запускаете минимизатор несколько раз, чтобы увидеть, сходится ли он.
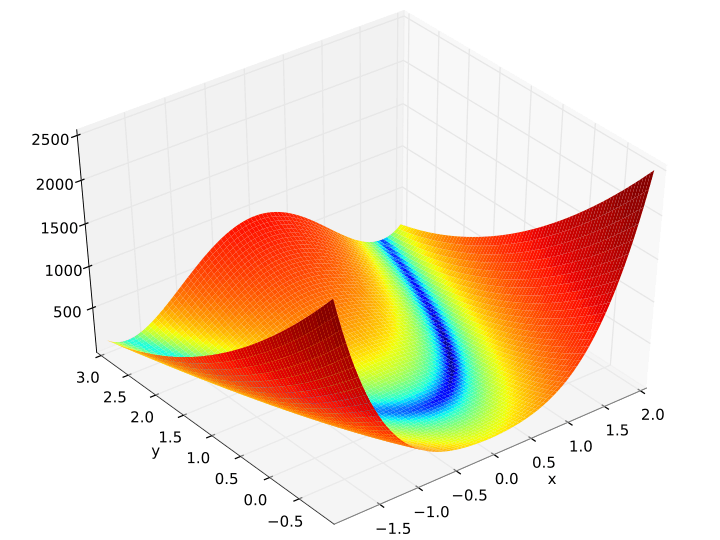
- Представьте, что мяч катится по склону. Это проблема оптимизации. Идея "минимизатора" состоит в том, чтобы найти значение, которое уменьшает градиент / наклон или производную. Другими словами, вы находите, где мяч в конечном итоге лежит. Задачи оптимизации могут стать более интересными и сложными, особенно если шарик катится в седловую точку или локальный минимум (не глобальный минимум) или вдоль горизонтального гребня или плоскости, для которой минимум почти невозможно найти. Например, рассмотрим знаменитую функцию Розенброка (см. Изображение), двумерную поверхность, где найти долину несложно, но найти минимум сложно.
fminа такжеminimizeфункции почти эквивалентны для симплексного алгоритма. Тем не мение,fminменее устойчив для сложных функций.minimizeобобщается для других алгоритмов, например, "Nelder-Mead" (симплекс), "Powell", "CG" и т. д. Эти алгоритмы представляют собой просто разные подходы для "толкания" или ускорения движения мяча вниз к минимуму. Кроме того, предоставление матрицы Якоби и Гессе в качестве параметров дляminimumФункция повышает эффективность вычислений. Посмотрите документы Scipy для получения дополнительной информации о том, как используются эти функции.