Рассчитать отставание от фазы стрелок с бивавелетом в r

Question

Я пытаюсь понять функцию перекрестного вейвлета в R, но не могу понять, как преобразовать стрелки фазовой задержки в временную задержку с помощью пакета biwavelet. Например:

require(gamair)
data(cairo)
data_1 <- within(cairo, Date <- as.Date(paste(year, month, day.of.month, sep = "-")))
data_1 <- data_1[,c('Date','temp')]
data_2 <- data_1

# add a lag
n <- nrow(data_1)
nn <- n - 49
data_1 <- data_1[1:nn,]
data_2 <- data_2[50:nrow(data_2),]
data_2[,1] <- data_1[,1]

require(biwavelet)
d1 <- data_1[,c('Date','temp')]
d2 <- data_2[,c('Date','temp')]
xt1 <- xwt(d1,d2)
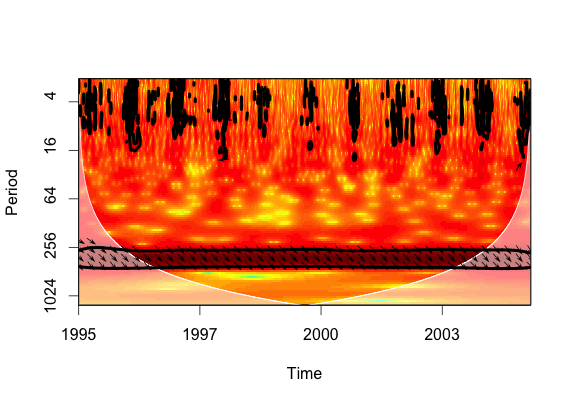
plot(xt1, plot.phase = TRUE)

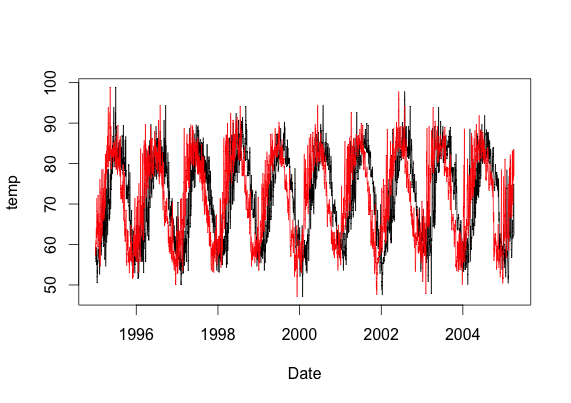
Это мои два временных ряда. Оба идентичны, но один отстает от другого. Стрелки указывают на фазовый угол 45 градусов - очевидно, что направление вниз или вверх означает 90 градусов (в фазе или вне фазы), поэтому я понимаю, что я смотрю с задержкой в ​​45 градусов.

Как бы я теперь преобразовал это во временную задержку, т.е. как бы я вычислил временную задержку между этими сигналами?

Я читал в Интернете, что это может быть сделано только для определенной длины волны (что, я полагаю, означает для определенного периода?). Итак, учитывая, что мы заинтересованы в периоде 365, а временной интервал между сигналами составляет один день, как можно рассчитать временную задержку?

Answer 1

В моем случае для приливной волны в полусуточный период 90 градусов равен 3 часам (90*12,5 часов / 360 = 3,125 часа). 12,5 часов - это полусуточный период. Итак, для 45 градусов, равных -> 45*12,5 / 360 = 1,56 часа.

Таким образом, в вашем случае: 90 градусов -> 90*365/360 = 91,25 часа. 45 градусов -> 45*365/360= 45,625 часов.

Answer 2

Мое понимание таково: для существования простой причинно-следственной связи между явлениями, зарегистрированными во временных рядах, мы должны ожидать, что колебания синхронизированы по фазе (Grinsted 2004); поэтому период, в котором вы найдете стрелку «в фазе» (--->), указывает на задержку между сигналами.

См. смоделированные примеры с разным расстоянием между причинно-следственными явлениями; обратите внимание, что чем больше расстояние, тем больше период появления «синфазной стрелки» в перекрестном вейвлет-преобразовании.

Нелинейные процессы в геофизике (2004) 11: 561–566 SRef-ID: 1607-7946/npg/2004-11-561

См. пример здесь

Answer 3

Поэтому я полагаю, что вы спрашиваете, как вы можете определить, какое время задержки дается двум временным рядам (в данном случае вы искусственно добавили задержку в 49 дней).

Мне не известны какие-либо пакеты, которые делают это одностадийным процессом, но, поскольку мы, по сути, имеем дело с волнами греха, одним из вариантов будет "обнуление" волн и затем поиск точек пересечения нуля. Затем вы можете рассчитать среднее расстояние между точками пересечения нуля волны 1 и волны 2. Если вам известен временной шаг между измерениями, вы можете легко рассчитать время задержки (в этом случае время между этапами измерения составляет один день).

Вот код, который я использовал для этого:

#smooth the data to get rid of the noise that would introduce excess zero crossings)
#subtracted 70 from the temp to introduce a "zero" approximately in the middle of the wave
spline1 <- smooth.spline(data_1$Date, y = (data_1$temp - 70), df = 30)
plot(spline1)
#add the smoothed y back into the original data just in case you need it
data_1$temp_smoothed <- spline1$y

#do the same for wave 2
spline2 <- smooth.spline(data_2$Date, y = (data_2$temp - 70), df = 30)
plot(spline2)
data_2$temp_smoothed <- spline2$y

#function for finding zero crossing points, borrowed from the msProcess package
zeroCross <- function(x, slope="positive")
{
  checkVectorType(x,"numeric")
  checkScalarType(slope,"character")
  slope <- match.arg(slope,c("positive","negative"))
  slope <- match.arg(lowerCase(slope), c("positive","negative"))

  ipost  <- ifelse1(slope == "negative", sort(which(c(x, 0) < 0 & c(0, x) > 0)),
  sort(which(c(x, 0) > 0 & c(0, x) < 0)))
  offset <- apply(matrix(abs(x[c(ipost-1, ipost)]), nrow=2, byrow=TRUE), MARGIN=2, order)[1,] - 2
  ipost + offset
}

#find zero crossing points for the two waves
zcross1 <- zeroCross(data_1$temp_smoothed, slope = 'positive')
length(zcross1)
[1] 10

zcross2 <- zeroCross(data_2$temp_smoothed, slope = 'positive')
length(zcross2)
[1] 11

#join the two vectors as a data.frame (using only the first 10 crossing points for wave2 to avoid any issues of mismatched lengths)
zcrossings <- as.data.frame(cbind(zcross1, zcross2[1:10]))

#calculate the mean of the crossing point differences
mean(zcrossings$zcross1 - zcrossings$V2)
[1] 49

Я уверен, что есть более красноречивые способы сделать это, но он должен дать вам информацию, которая вам нужна.