Коэффициенты B-Spline Curves - деление на ноль (код в DELPHI)

Question

Я пытался реализовать следующую рекурсивную формулу для моего кода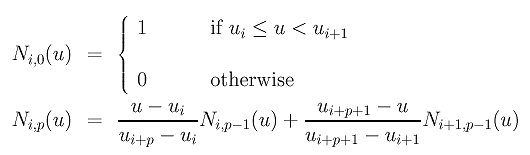

но к моему удивлению оказывается, что после реализации этого в DELPHI, я получаю ошибку из-за деления на ноль. Я на 98% уверен, что мой вектор узлов рассчитан правильно, что означает, что деления на ноль не должно быть. Я на 70% уверен, что рекурсивная формула правильно реализована, поэтому я публикую здесь свой код:

program project1;

uses
SysUtils;

Type
  TRealPoint = record
    x: single;
    y: single;
  end;

type
  TSample = Class(TObject)
    public
      KnotVector: array of single;
      FitPoints: array of TRealPoint;
      Degree: integer;
      constructor Create; overload;
      function Coefficient(i, p: integer; Knot: single): single;
      procedure GetKnots;
      destructor Destroy; overload;
  end;

constructor TSample.Create;
begin
  inherited;
end;

function TSample.Coefficient(i, p: integer; Knot: single): single;
var
  s1, s2: single;
begin
   If (p = 0) then
   begin
     If (KnotVector[i] <= Knot) And (Knot < KnotVector[i+1]) then Result := 1.0
     else Result := 0.0;
   end
   else
   begin
     s1 := (Knot - KnotVector[i])*Coefficient(i, p-1, Knot)/(KnotVector[i+p] - KnotVector[i]); //THIS LINE ERRORS due to division by zero ???
     s2 := (KnotVector[i+p+1]-Knot)*Coefficient(i+1,p-1,Knot)/(KnotVector[i+p+1]-KnotVector[i+1]);
     Result := s1 + s2;
   end;
end;

procedure TSample.GetKnots();
var
  KnotValue: single;
  i, MaxKnot: integer;
begin
  // KNOTS
  KnotValue:= 0.0;
  SetLength(KnotVector, Length(FitPoints) + 1 + Degree);
  MaxKnot:= Length(KnotVector) - (2*Degree + 1);
  for i := Low(KnotVector) to High(KnotVector) do
  begin
    if i <= (Degree) then KnotVector[i] := KnotValue / MaxKnot
    else if i > Length(FitPoints) then KnotVector[i] := KnotValue / MaxKnot
    else
    begin
      KnotValue := KnotValue + 1.0;
      KnotVector[i] := KnotValue / MaxKnot;
    end;
  end;
end;

destructor TSample.Destroy;
begin
   inherited;
end;

var
  i, j: integer;
  Test: TSample;
  N: array of array of single;
begin
  Test := TSample.Create;
  //define degree
  Test.Degree := 3;
  //random fit points
  j := 15;
  SetLength(Test.FitPoints, j + 1 + Test.Degree);
  For i := Low(Test.FitPoints) to High(Test.FitPoints) do
  begin
    Test.FitPoints[i].x := Random()*2000;
    Test.FitPoints[i].y := Random()*2000;
  end;
  //get knot vector
  Test.GetKnots;
  //get coefficients
  SetLength(N, j+1, j+1);
  For j := Low(N) to High(N) do
  begin
    For i := Low(N[j]) to High(N[j]) do
      begin
        N[j, i] := Test.Coefficient(i,3,Test.KnotVector[j]);
        write(floattostrf(N[j,i], ffFixed, 2, 2) + ', ');
      end;
    writeln();
  end;
  readln();
  Test.Free;
end.

В основном я не уверен, как продолжить. Мне бы понадобились значения матрицы N ( см. Эту ссылку) базисных коэффициентов, но каким-то образом использование формулы из этой ссылки приводит меня к делению на ноль.

Итак... Есть ли совершенно другой способ, как рассчитать эти коэффициенты или в чем здесь проблема?

ОБНОВИТЬ

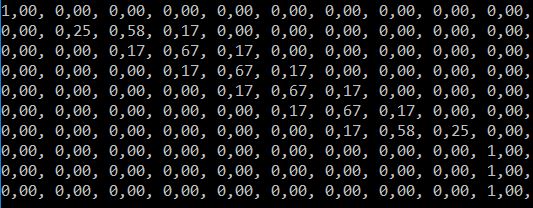
Вместо того, чтобы использовать мою собственную идею, я попытался реализовать алгоритм отсюда, как это было предложено Dsm в комментариях. В результате больше нет деления на ноль, но в любом случае результат совершенно неожиданный.

Для n + 1 = 10 случайных точек подгонки со степенью 3 сплайна базовая матрица N (см. Ссылку) является единственной - как видно из прилагаемого изображения.

Вместо этого я бы ожидал, что матрица будет зонной матрицей. В любом случае, вот мой обновленный код:

program project1;

uses
SysUtils;

Type
  TRealPoint = record
    x: single;
    y: single;
  end;

type
  TMatrix = array of array of double;

type
  TSample = Class(TObject)
    public
      KnotVector: array of double;
      FitPoints: array of TRealPoint;
      SplineDegree: integer;
      Temp: array of double;
      A: TMatrix;
      procedure GetKnots;
      function GetBasis(Parameter: double): boolean;
      procedure FormBasisMatrix;
  end;

procedure TSample.GetKnots();
var
  i, j: integer;
begin
  // KNOTS
  //https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/INT-APP/PARA-knot-generation.html
  SetLength(KnotVector, Length(FitPoints) + SplineDegree + 1);
  for i := Low(KnotVector) to High(KnotVector) do
  begin
    if i <= SplineDegree then KnotVector[i] := 0
    else if i <= (High(KnotVector) - SplineDegree - 1) then KnotVector[i] := (i - SplineDegree) / (Length(FitPoints) - SplineDegree)
    else KnotVector[i] := 1;
  end;
end;

function TSample.GetBasis(Parameter: double): boolean;
var
  m, d, k: integer;
  FirstTerm, SecondTerm: double;
begin
  //http://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/B-spline/bspline-curve-coef.html
  Result := False;
  //initialize to 0
  SetLength(Temp, Length(FitPoints));
  For m := Low(Temp) to High(Temp) do Temp[m] := 0.0;
  //special cases
  If Abs(Parameter - KnotVector[0]) < 1e-8 then
  begin
    Temp[0] := 1;
  end
  else if Abs(Parameter - KnotVector[High(KnotVector)]) < 1e-8 then
  begin
    Temp[High(Temp)] := 1;
  end
  else
  begin
    //find knot span [u_k, u_{k+1})
    for k := Low(KnotVector) to High(KnotVector) do if Abs(KnotVector[k] - Parameter) < 1e-8 then break;
    Temp[k] := 1.0;
    for d := 1 to SplineDegree do
    begin
      Temp[k - d] := (KnotVector[k + 1] - Parameter) * Temp[k - d + 1] / (KnotVector[k + 1] - KnotVector[k - d + 1]);
      for m := k - d + 1 to k - 1 do
      begin
        FirstTerm := (Parameter - KnotVector[m]) / (KnotVector[m + d] - KnotVector[m]);
        SecondTerm := (KnotVector[m + d + 1] - Parameter) / (KnotVector[m + d + 1] - KnotVector[m + 1]);
        Temp[m] := FirstTerm * Temp[m] + SecondTerm * Temp[m + 1];
      end;
      Temp[k] := (Parameter - KnotVector[k]) * Temp[k] / (KnotVector[k + d] - KnotVector[k]);
    end;
  end;
  Result := True;
end;

procedure TSample.FormBasisMatrix;
var
  i, j: integer;
begin
  SetLength(A, Length(FitPoints), Length(FitPoints));
  for j := Low(A) to High(A) do
  begin
    for i := low(A[j]) to High(A[j]) do //j - row, i - column
    begin
      If GetBasis(KnotVector[j + SplineDegree]) then A[j, i] := Temp[i];
    end;
  end;
end;


var
  i, j, iFitPoints: integer;
  Test: TSample;
  N: array of array of single;
begin
  Test := TSample.Create;
  //define degree
  Test.SplineDegree := 3;
  //random fit points
  iFitPoints := 10;
  SetLength(Test.FitPoints, iFitPoints);
  For i := Low(Test.FitPoints) to High(Test.FitPoints) do
  begin
    Test.FitPoints[i].x := Random()*200;
    Test.FitPoints[i].y := Random()*200;
  end;
  //get knot vector
  Test.GetKnots;
  //get B-Spline basis matrix
  Test.FormBasisMatrix;
  // print matrix
  for j := Low(Test.A) to High(Test.A) do
  begin
    for i := Low(Test.A) to High(Test.A) do write(FloatToStrF(Test.A[j, i], ffFixed, 2, 2) + ', ');
    writeln();
  end;
  readln();
  Test.Free;
end.

Answer 1

Это не полный ответ, но он может помочь вам на вашем пути, и результат будет ближе к тому, что вы ожидаете, но, как я говорю, не полностью там.

Прежде всего, узлы выглядят не так, как мне. Кажется, что узлы образуют функцию "линейного изменения" (фиксированная линия), и хотя я не могу понять, имеет ли "m" какое-либо конкретное значение, я бы ожидал, что функция будет непрерывной, а ваша нет. Делая это непрерывно дает лучшие результаты, например

procedure TSample.GetKnots();
var
  i, j: integer;
  iL : integer;
begin
  // KNOTS
  //https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/INT-APP/PARA-knot-generation.html
  iL := Length( FitPoints );
  SetLength(KnotVector, iL + SplineDegree + 1);
  // set outer knot values and sum used to geterate first internal value
  for i := 0 to SplineDegree - 1 do
  begin
    KnotVector[ i ] := 0;
    KnotVector[ High(KnotVector)-i] := 1;
  end;
  // and internal ones
  for i := 0 to High(KnotVector) - 2* SplineDegree + 1 do
  begin
    KnotVector[ SplineDegree + i - 1] := i / (iL - 1);
  end;
end;

Я ввел iL = Length( Fitpoints) для удобства - это не важно.

Вторая проблема, которую я обнаружил, - это скорее проблема программирования. В процедуре GetBasis вы оцениваете k, прерывая цикл for. Проблема в том, что k не гарантированно будет сохраняться вне цикла, поэтому использование его позже не обязательно будет успешным (хотя может и)

Наконец, там же, на мой взгляд, определение вашего диапазона совершенно неверно. Вы должны искать параметр, лежащий в половине открытого отрезка, но вместо этого вы ищете, чтобы он находился близко к конечной точке этой линии.

Положить эти два вместе

   for k := Low(KnotVector) to High(KnotVector) do if Abs(KnotVector[k] - Parameter) < 1e-8 then break;

должен быть заменен

k1 := 0;
for k1 := High(KnotVector) downto Low(KnotVector)  do
begin
  if Parameter >= KnotVector[k1] then
  begin
   k := k1;
   break;
  end;
end;

где k1 - целое число

Я не могу не чувствовать, что где-то есть ошибка плюс 1, но я не могу ее обнаружить.

В любом случае, я надеюсь, что это поможет вам продвинуться немного дальше.

Answer 2

Чтобы построить рекурсивную пирамиду для вычисления коэффициентов через интервалы, вы должны начать верхний уровень рекурсии (внутренний цикл вычислений) с первого реального (не дублирующего) индекса узла:

 For i := Test.Degree...

Также проверьте индекс последнего цикла.

PS можно удалить constructor а также destructor из описания класса и реализации, если у них нет ничего, кроме inherited,