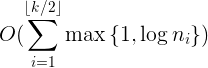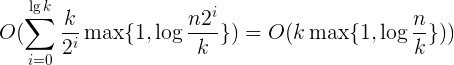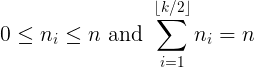Сложность heapify в левой очереди кучи
"Структуры данных и сетевые алгоритмы" Тарьяна заявляют функцию heapify в самых маленьких кучах следующим образом:
heap function heapify (list q);
do |q| ≥ 2 → := q[3..] & meld (q(1), q(2)) od;
return if q = [ ] → null | q != [ ] → q(1) fi
end heapify;
q это очередь кучи, которую мы хотели бы сложить вместе. meld(h1, h2) является функцией для объединения двух куч и восстановления свойства кучи. meld(h1, h2) имеет сложность O (logn), где n - общее количество узлов в обеих кучах. Это усложняет один проход через очередь следующим образом:
что правдоподобно. Что я не получаю, так это время для всей кучи, как есть:
k вот количество оригинальных куч и n общее количество предметов, которые они содержат. Есть также два ограничения, упомянутых заранее:
Может кто-нибудь помочь мне понять, как уравнение. 2 выводится? (как интерпретировать левое выражение равенства в уравнении 2)
1 ответ
Я разобрался с решением, которое оказалось довольно очевидным:
в каждой итерации число элементов очереди уменьшается вдвое. Это делает это k / 2 за итерацию. Глядя на все итерации, число экспоненциально уменьшается до основания 2, т. Е. Для i=0 имеем k; i=1 к /2; i=2 к /4; i=3 k/8 и т. д. Поэтому сумма увеличивается до lg k, а количество куч уменьшается на k/(2^i). Сумма в формуле 3 говорит нам, что все элементы распределены между кучами текущего цикла. Как мы только что выяснили, количество куч на одну итерацию равно k/(2^i). Вот почему максимум для слияния за очередь составляет n_i = n/(k/(2_i)) = n*(2_i)/k. Все это вместе объясняет уравнение. 2 и после отбрасывания констант получаем уравнение на правой стороне.